Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Проверка гипотезы о том, что результаты наблюдений принадлежат нормальному распределению.
|
|
Доверительные границы случайной погрешности результата измерения устанавливают для результатов наблюдений, принадлежащих нормальному распределению.
При числе результатов наблюдений n > 50 для проверки принадлежности их к нормальному распределению предпочтительным является один из критериев: χ 2 Пирсона или ω 2 Мизеса - Смирнова.
При числе результатов наблюдений 50 > n > 15 для проверки принадлежности их к нормальному распределению предпочтительным является составной критерий.
Критерий 1. Вычисляют отношение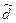 
,
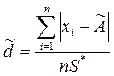где S* - смещенная оценка среднего квадратического отклонения, вычисляемая по формуле
Результаты наблюдений группы можно считать распределенными нормально, если
,
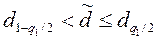где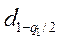 
и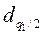 
- квантили распределения, получаемые из табл. 1 по n, q 1/2 и (1 – q 1/2
Проверку гипотезы о том, что результаты наблюдений принадлежат нормальному распределению, следует проводить с уровнем значимости q от 10 до 2 %. Конкретные значения уровней значимости должны быть указаны в конкретной методике выполнения измерений.
Критерий 2. Можно считать, что результаты наблюдений принадлежат нормальному распределению, если не более m разностей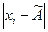 
превзошли значение zp/2 S, где S - оценка среднего квадратического отклонения, вычисляемая по формуле
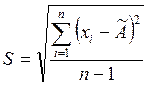
Таблица 1
Статистика d
| N | q 1/2 100% | (1- q 1/2) 100% | ||
| 1 % | 5 % | 95 % | 99 % | |
| 0, 9137 | 0, 8884 | 0, 7236 | 0, 6829 | |
| 0, 9001 | 0, 8768 | 0, 7304 | 0, 6950 | |
| 0, 8901 | 0, 8686 | 0, 7360 | 0, 7040 | |
| 0, 8826 | 0, 8625 | 0, 7404 | 0, 7110 | |
| 0, 8769 | 0, 8578 | 0, 7440 | 0, 7167 | |
| 0, 8722 | 0, 8540 | 0, 7470 | 0, 7216 | |
| 0, 8682 | 0, 8508 | 0, 7496 | 0, 7256 | |
| 0, 8648 | 0, 8481 | 0, 7518 | 0, 7291 |
где zp/2 - верхний квантиль распределения нормированной функции Лапласа, отвечающий вероятности Р/2.
Значения Р определяются из табл. 2 по выбранному уровню значимости q2 и числу результатов наблюдений n.
При уровне значимости, отличном от предусмотренных в табл. 2, значение Р находят путем линейной интерполяции.
В случае, если при проверке нормальности распределения результатов наблюдений группы для критерия 1 выбран уровень значимости q 1, а для критерия 2 - q 2, то результирующий уровень значимости составного критерия
q ≤ q 1 + q 2.
В случае, если хотя бы один из критериев не соблюдается, то считают, что распределение результатов наблюдений группы не соответствует нормальному.
При числе результатов наблюдений n ≤ 15 принадлежность их к нормальному распределению не проверяют. При этом нахождение доверительных границ случайной погрешности результата измерения возможно в том случае, если заранее известно, что результаты наблюдений принадлежат нормальному распределению
Таблица 2