Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Глава 7. Волны
|
|
Здесь мы, наконец, оставим изучение механики и посвятим краткую паузу волновому движению. Можно резонно предположить, что раз используется слово движение, то и основным предметом этой главы будет по-прежнему механика. Однако волна – это очень специфическое понятие, которое появляется в физике во многих обличиях. Особенно это относится к физике двадцатого столетия, знакомству с которой будет посвящена оставшаяся часть этой книги. Понимание основ волнового языка, то есть языка, на котором описываются волновые процессы, является абсолютно необходимым для дальнейшего чтения.
Распространение волн — это не механическое явление. В первую очередь из-за того, что волна — это не материальный объект, а форма существования материи. Волне нельзя приписать какую- либо массу, а понятие ускорение абсолютно бесполезно для того, чтобы иметь дело с волнами. Волновое движение принципиально отличается от тех движений среды, в которой волна перемещается. Более того, существуют волны, распространение которых происходит вообще без какого-либо движения частиц среды (электромагнитные волны). Любая волна, независимо от ее физической природы, подчиняется своим собственным, волновым, законам.
Итак, что же такое волна? Это – особое локальное состояние среды, картина, (pattern [38]), которая перемещается в пространстве, модель иформа этого движения. Это может быть и локальная деформация материального объекта – так, как это происходит в случае удара по натянутой струне музыкального инструмента, или же при создании возмущения на поверхности воды. Волна может быть и состоянием поля, как это бывает в случае световых и радиоволн. Конечно же, приведенные примеры не исчерпывают список всех волновых явлений.
Одиночная волна*
Эту главу мы начнем с рассмотрения волн в их самом простом проявлении — с перемещения локального возмущения, или “ волнового импульса”, по одномерному объекту, подобному струне музыкального инструмента. Потом мы перейдем к непрерывным, периодическим волнам, а затем и к волнам в пространстве двух (2d -) и трех (3d -) измерений, выстраивая тем самым объяснение эксперимента, который демонстрирует волновую природу света.
Нет никакого смысла двигаться дальше, не приводя конкретных примеров. Мы начнем с самого простого — с рассмотрения одиночноговолнового импульса. Самый наглядный способ представить его возникновение — это вообразить короткий и резкий удар (или “ щипок ”) по туго натянутой струне. До удара струна образует прямую линию. Если внешнее воздействие искажает форму струны, то возникающие в струне напряжения будут стремиться вернуть струне первоначальную форму (см. рис. 7 - 1).
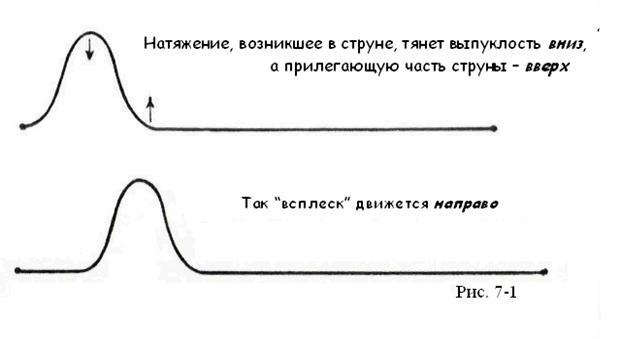
Применим третий закон Ньютона: если та часть струны, которая оказалась справа (по рис. 7-1) от места удара, “тянет” образовавшуюся на струне выпуклость вниз, то с той же силой, эта выпуклость тянет правую часть струны вверх! Этот процесс продолжается постоянно и, в результате, к тому времени, когда первоначальный след от удара исчезнет, справа[39] от него на струне возникнет движущаяся вправо выпуклость (“след” от удара, возмущение). Отметим, что движется именно волновой импульс (“след” от удара), а не сама струна. Элементы (частицы) струны лишь на время прохождения импульса смещаются в направлении перпендикулярном его движению, а после прохождения волны возвращаются обратно на свои места, вновь образуя прямую линию.
Нет никакой необходимости останавливаться на описании подробностей и деталей (особенно математических) процесса распространения импульса вдоль струны. Да, реальное движение струны вызывает идругое наблюдаемое волновое движение — после удара в струне возникают два волновых импульса: один будет двигаться вправо, а другой – влево. Мы увидим вскоре, что можно полностью понять такое движение волновых импульсов, не беспокоясь о деталях движения самой струны. Движение средыможно не рассматривать при изучении волновых процессов.
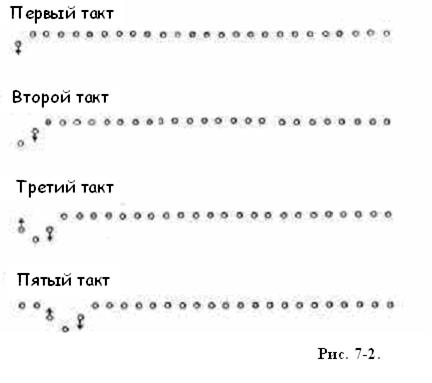Чтобы сделать эту мысль более понятной, рассмотрим ещё один пример, абсолютно свободный от любой связи с законами механики. Вообразим военный духовой оркестр, построенный в одну шеренгу. Каждому музыканту дана инструкция: " смотри на своего соседа справа и повторяй его движения в следующем такте”. Затем мы подходим к началу шеренги и просим стоящего там музыканта сделать два шага вперед, а потом сразу вернуться на место, сделав два шага назад.
Первые фазы возникающего в шеренге эффекта иллюстрирует рис. 7 - 2 (вид сверху на шеренгу музыкантов). Неоднородность, " всплеск" в шеренге перемещается слева направо, но ни один из музыкантов не смещается при этом ни влево, ни вправо. И это ни в коем случае не аналогия, а реальное проявление волны в полном значении этого слова[40], за исключением того, что " среда", в которой распространяется эта волна, дискретна (не непрерывна). В большинстве случаев, которые нам предстоит рассматривать далее, речь пойдет о волнах, которые распространяются в непрерывных, сплошных средах, однако наши базовые знания о волнах, их законах и свойствах могут быть применены ко всем волнам, существующим в природе.
Это дает нам возможность зафиксировать важнейшее свойство волн: волны распространяются с постоянной скоростью, которая зависит от природы среды, но не от самой волны. В нашем примере волна за один музыкальный такт сдвигается на расстояние равное дистанции между музыкантами в шеренге. Это происходит из-за действия тех инструкций, которые даны музыкантам, и не зависит от формы волны. Если бы мы попросили, чтобы первый в шеренге музыкант сделал не два, а три шага вперед, а потом три шага назад, то была бы сформирована волна с бó льшим размахом, но она все равно распространялась бы по шеренге с той же самой скоростью. Фактически, основным (базовым) понятием в теории волн является представление о волне, которая распространяется с постоянной скоростью, не изменяя своей формы.
Таким образом, нет никакой надобности доказывать, что волна распространяется по струне с постоянной скоростью не изменяя своей формы. Если вдруг обнаружится, что это не так, то это просто покажет, что струна — плохой пример для рассмотрения волновых явлений. Однако в действительности хорошо натянутая струна, это превосходная среда для изучения распространения волн. Так, например, если струна сильно натянута, а сама струна тонкá, то те ускорения, с которыми элементы струны возвращаются из деформированного состояния, будут велики, и волна будет быстро перемещаться по струне. Если же, напротив, струна будет массивной или же слабо натянутой, то волна будет двигаться по струне медленнее[41].