Суперпозиция (наложение) волн

Существует универсальный закон, который играет решающую роль в исследовании волновых процессов. Роль этого закона сопоставима со значением законов Ньютона в механике. Этот закон обычно называют: принцип суперпозиции. Само название напоминает уже рассмотренный ранее (Глава 3) принцип суперпозициив механике, однако, если в механике этот принцип является лишь средством для рассмотрения сложных движений, то в теории волн этот принцип имеет основополагающее значение. В волновой теории принцип суперпозиции отражает тот факт, что присутствие одной волны не изменяет способность среды нести другую волну.

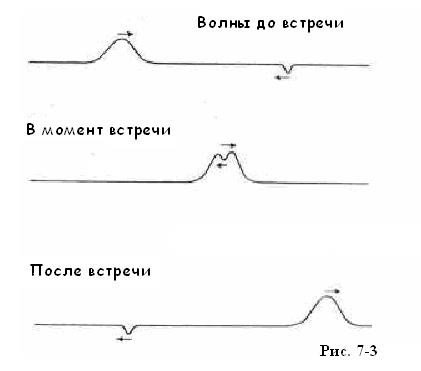
Таким образом, две волны, распространяющиеся в одной и той же среде, могут пройти сквозь друг друга, не изменив своей формы. Простой пример для случая двух волн, бегущих по струне навстречу друг другу показан на рис. 7-3. В момент встречи волн маленькая волна проявляет себя просто как небольшой провал на большой волне.

Если использовать не качественные(“маленькая волна”, “небольшой провал”), а количественные характеристики, то волновой принцип суперпозиции позволяет утверждать, что смещение, произведенное несколькими волнами воднойи той же точке, является суммой смещений, производимых каждой из волн. Наиболее интересно применение этого принципа к волнам одинакового размера (одинаковой амплитуды [42], а,). Рис. 7-4 иллюстрирует проявление принципа суперпозиции для двух одинаковых волн, распространяющихся навстречу друг другу.
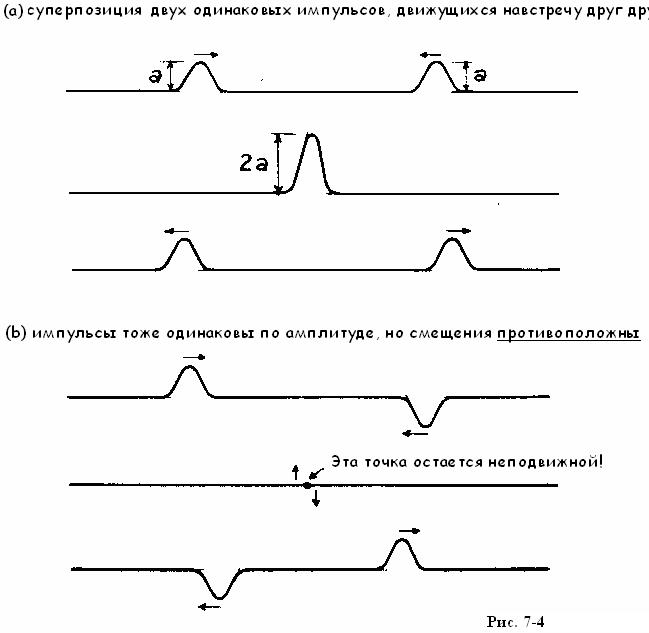На рис.7-4 (b) волны тоже одинаковы по амплитуде, но их смещения противоположны друг другу. Этот случай наиболее поучителен — в течение очень короткого момента времени при встрече двух волн струна оказывается абсолютно плоской. Но как только элемент струны, лежащий чуть левее точки встречи волн начнет двигаться вниз, а симметричный ему (и лежащий чуть правее точки встречи волн) сегмент, начнет двигаться вверх, то первоначальный образ двух волн, движущихся навстречу друг другу, будет очень быстро восстановлен! Небольшое мыслительное усилие покажет, что на струне существует точка, лежащая ровно посередине двух полностью наложившихся друг на друга в момент встречи импульсов, которая не смещается вообще. (см.рис.7-4).

Одновременное присутствие двух[43] волн в одном месте называют интерференцией [44]. Если обе волны стремятся сместить точки среды в одном направлении (как на рис.7-4 a), то интерференцию называют конструктивной. Процессы, показанные на рис. 7-4b) соответствуют случаю деструктивной (разрушительной) интерференции.

Единственная связь между механическим и волновым принципамисуперпозициизаключается в том, что для механических волн (таких, как волны в струне, волны на поверхности воды и т.п.) волновой принцип суперпозиции может быть получен, как следствие механического. Но многие волны являются сугубо не механическими, так что лучше рассматривать принцип суперпозиции как особый волновой закон.

Наиболее интересные результаты дает " обратное" применение принципа суперпозиции. Это те ситуации, в которых мы анализируем волну и пытаемся предсказать её будущее развитие, представив ее в виде суммы нескольких других волн. Такой подход напоминает действия Галилея в ситуации, где он, анализируя движение снаряда, разложил сложное движение на два более простых (см. Гл. 3).

Вернемся к примеру, где волна создается резким ударом по середине натянутой струны. Сформированный ударом волновой импульс одинаково свободно перемещается в обоих направлениях. Создать на струне волну, движущуюся только вправо или только влево невозможно! Как это объяснить?

Нетрудно ответить на этот вопрос, если принять во внимание, что в момент резкого удара на струне реализуется точно такая же ситуация, как и в момент полного наложения двух одинаковых импульсов, бегущих навстречу друг другу (см рис. 7-4 (a)). В этих двух ситуациях нет никаких отличий ни в форме струны, ни в характере движения отдельных её элементов. Да, в одном случае “всплеск“ формируется в результате наложения двух бегущих волн, а в другом создается внешним воздействием, но не может быть никаких различий в последующем поведении волны. На основании этого мы можем предсказать, что “всплеск“ на струне, вызванный ударом по ней, неизбежно “расколется” на две волны, распространяющиеся по струне в противоположных направлениях. Очередное мыслительное усилие покажет, что амплитуда (“высота”) каждой из этих волн должна быть равна половине высоты начального “всплеска“. Наблюдения подтверждают, что дело обстоит именно так.