
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Нелинейная парная регрессия
|
|
Основным способом отыскания уравнения нелинейной регрессии (как и линейной) служит принцип наименьших квадратов. Это значит, что уравнение ищется в заданном классе функций и выборочные числовые данные используются лишь для определения неизвестных коэффициентов из системы нормальных уравнений. При этом различаются 2 случая: тип уравнения фиксируется сразу, так что принцип наименьших квадратов используется лишь один раз, или же уравнение регрессии в дальнейшем подвергается уточнениям, для чего принцип наименьших квадратов последовательно используется несколько раз.
Уравнение регрессии может быть известно заранее из соображений аналогии, из теоретических рассуждений или из сравнения эмпирических данных с известными формулами. Разумеется, никакая уверенность в типе регрессии не освобождает от регрессионного и корреляционного анализа найденного уравнения.
Известно, что любая непрерывная функция может быть со сколь угодно высокой точностью заменена многочленом, при этом повышение точности достигается за счет повышения степени многочлена. Поэтому на практике любую регрессию можно считать в виде многочлена, находя его степень путем последовательных подсчетов.
Но степень может оказаться очень высокой и в уравнении будет много неопределенных коэффициентов. А каждый коэффициент накладывает лишнюю связь на выборку и это увеличивает дисперсию.
Иногда используют регрессию показательного, логарифмического, дробно–степенного, тригонометрического и т.д. типов. Количество коэффициентов при этом сокращается, но подбор вида уравнения гораздо сложнее (нет соответствующего алгоритма).
При подборе формул можно руководствоваться следующими соображениями:
1) В тех случаях, когда с возрастанием одной величины замечается пропорциональное возрастание или убывание другой величины, прежде всего берется уравнение прямой
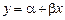 .
.
2) Если с возрастанием одной величины наблюдается резкое возрастание другой, то может быть применимо уравнение показательной кривой
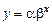 .
.
3) Если, наоборот, с возрастанием одной величины имеется замедленное возрастание другой, то может быть пригодна логарифмическая кривая
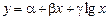 .
.
4) В случае периодического изменения одной величины с возрастанием другой могут быть применимы различные тригонометрические функции.
5) Для дугообразных кривых, имеющих один изгиб сравнительно хорошее совпадение может дать парабола 2–го порядка:
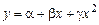 .
.
6) Для кривых S–образной формы, имеющих двойной изгиб, может подойти уравнение параболы 3–го порядка
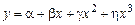 .
.
Вычисление трансцендентной регрессии упрощается, если провести замену переменных, превращающую регрессию в линейную. Например, зависимость показательного типа
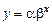
превращается в линейную путем логарифмирования
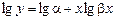 .
.