Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. Для такого сигнала вычисления АКФ удобнее и проще
|
|
Корреляционный анализ
Детерминированных сигналов
Корреляционный анализ наряду со спектральным играет важную роль в теории сигналов. Этот вид анализа «пришёл» в радиотехнику в конце 40-х и начале 50-х годов прошлого века, а фундаментальная теорема Винера-Хинчина связала его и спектральный анализ в единое целое. В радиотехнике корреляционная теория используется, прежде всего, при исследовании случайных процессов, позволяя установить связь между корреляционными и спектральными свойствами случайных сигналов.
Для чего нужна корреляционная теория? Часто возникает задача
обнаружения одного сигнала в другом или в помехах. Для надежного
обнаружения полезных сигналов и применяется метод корреляции, основанный на корреляционной теории. Часто на практике оказывается полезным анализ характеристики, дающей представление о скорости изменения во времени, а также длительности сигнала без разложения его на гармонические составляющие.
Корреляционная функция является одной из основных характеристик
радиолокационных сигналов. Она характеризует потенциальные возможности радиолокационной станции по разрешению целей. При рассмотрении принципов работы импульсной РЛС было выявлено, что информацию об
обнаруженном объекте можно получить путём сравнения параметров излучаемого и отражённого (копии) сигналов.
Корреляция – это статистическая зависимость между явлениями и процессами. Корреляционная зависимость отличается от функциональной, выражающейся в общем виде как, тем, что в ней возможные последствия каких-либо событий могут быть измерены лишь приблизительно. Таким образом, при корреляционной зависимости переменная величина вызывает изменения другой величины лишь с определённой степенью вероятности, называемой коэффициентом корреляции.
Корреляционный анализ применяется в радиолокации, радиоастрономии, гидроакустике, сейсмологии и т.д. при решении задач обнаружения слабых сигналов, замаскированных шумами. Он используется также для определения спектральных характеристик сигналов и выявления их идентичности, что необходимо при исследованиях, связанных с измерением очень слабых сигналов.
Спектральный подход, несмотря на свою эффективность, не всегда является наиболее подходящим для анализа сигналов. На практике часто возникает необходимость в характеристике, которая давала бы общее представление об изменении сигнала во времени без разложения его на гармонические составляющие. Подобная «временнá я» характеристика особенно важна для анализа случайных сигналов и шумов, а также для обнаружения сигналов в шумах, когда решение о наличии сигнала принимается после сравнения смеси «сигнал + шум» с заранее известной копией принимаемого сигнала. Эта проблема особенно актуальна для обнаружения радиолокационных целей в условиях шумовых помех.
В теории корреляционного анализа используются понятия оригинала сигнала и его копии, сдвинутой по времени на некоторую величину 𝝉. В основе корреляционного анализа лежит понятие спектральной плотности сигналов, построенное на геометрических методах, применяемых в теории сигналов).
Пусть копия сигнала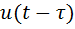 
(рис.1) смещена относительно своего оригинала 
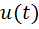на некоторый заданный интервал времени 
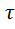. Для количественной оценки степени отличия (связи) исходного сигнала 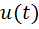и его смещённой во времени копии 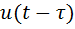используют автокорреляционную функцию (АКФ). Автокорреляционная функция показывает степень сходства между анализируемым сигналом и его сдвинутой копией – чем больше значение корреляционной функции, тем это сходство сильнее. Поэтому термин «автокорреляция» применяют, когда находят связь сигнала с его копией.
Для детерминированного сигнала конечной длительности (финитного сигнала) аналитическая запись АКФ представляет собой интеграл вида
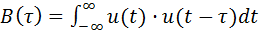................ (1)
Формула (1)показывает, что при отсутствии сдвига (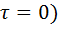
АКФ имеет положительное значение и достигает максимальной величины, равной энергии сигнала:
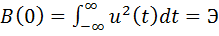...................... (2)
Такая энергия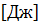 
выделяется на резисторе с сопротивлением в 1 Ом, если к его выводам подключить некоторое напряжение 
.
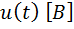Одним из важнейших свойств АКФ является её чётность т.е.
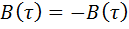, что достаточно просто доказывается математически. Действительно, если в выражении (1)произвести замену переменной 
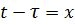, то
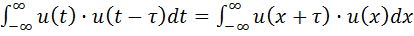
Поэтому интеграл (1) можно представить в другом виде:
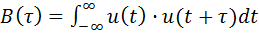......................... (3)
Для периодического сигнала АКФ определяется за период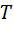 
:
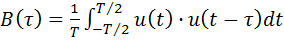.................. (4)
Пример. Определить АКФ прямоугольного импульса (рис. 1). Прямоугольный импульс имеет амплитуду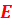 
и длительность 
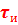(рис. 1, а).
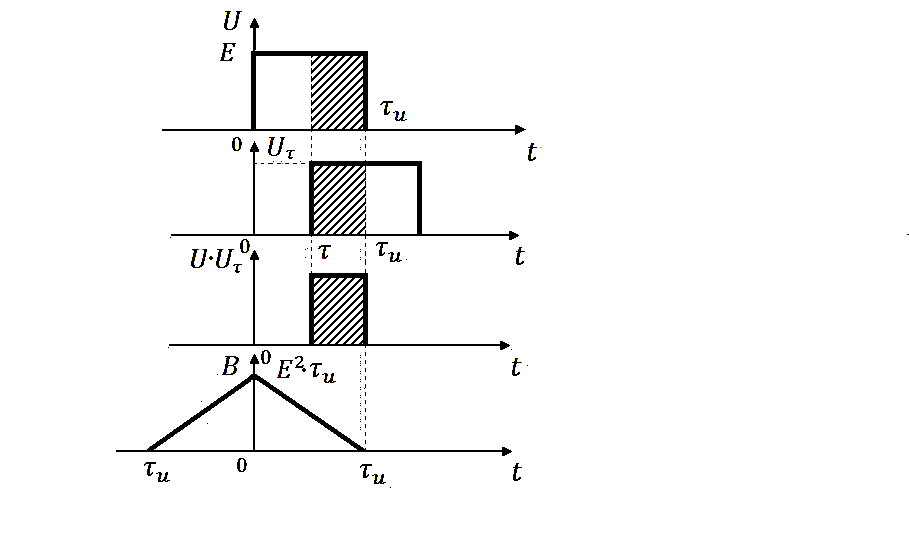
Рис.1. К определению автокорреляционной функции:
а) импульс; б) копия; в) произведение сигнала и копии; г) АКФ
(На последней эпюре горизонтальная ось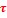 
)
Решение. Для такого сигнала вычисления АКФ удобнее и проще
провести графически. Такое построение показано на рис. 1, а - в, где приведены соответственно: исходный видеоимпульс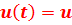 
, сдвинутая на 
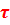его копия 
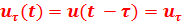и их произведение
Рассмотрим графическое вычисление интеграла (2.99). Очевидно, что произведение не равно нулю на интервале времени, когда имеется наложение друг на друга любых частей сигнала и его копии.
Как следует из рис. 1, этот интервал равен 
, если временной сдвиг копии меньше длительности импульса. В подобных случаях для прямоугольного импульса АКФ определится как