Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Связь между энергетическим спектром и АКФ сигнала
|
|
Допустим, что некоторый импульсный сигнал 
имеет спектральную плотность 
. С помощью формулы (1)определим АКФ, записав заданный сигнал в виде обратного преобразования Фурье:
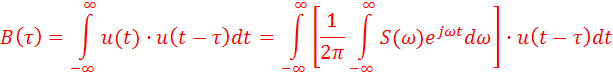
Для упрощения и удобства введём новую переменную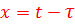 
.
Затем, сделав в последнем выражении ряд перестановок, получим
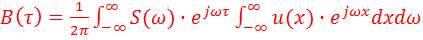............ (5)
Здесь интеграл
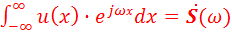......................... (6).
есть функция, комплексно-сопряжённая со спектральной плотностью сигнала . Поэтому формула (5)примет вид:
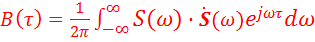................... (7).
Функцию
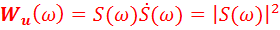........................ (8).
называют энергетическим спектром (спектральной плотностью энергии)
сигнала, который показывает распределение его энергии по оси частот. Физическая размерность энергетического спектра сигнала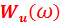 
измеряется в
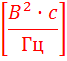
Учитывая соотношение (8), окончательно получим выражение для АКФ аналогового детерминированного сигнала
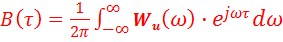.......................... (9).
Как следует из этого выражения, автокорреляционная функция представляет собой обратное преобразование Фурье от энергетического спектра.
Очевидно, что имеется и прямое преобразование Фурье от автокорреляционной функции:
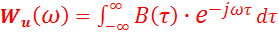.............................. (10).
Таким образом, можно сделать следующие выводы:
Ø Прямое преобразование Фурье (10) автокорреляционной функции детерминированного сигнала определяет его энергетический спектр;
Ø Обратное преобразование Фурье энергетического спектра (9) определяет автокорреляционную функцию детерминированного сигнала.
Данные результаты имеют фундаментальное значение в радиотехнике и важны по двум причинам.
Во-первых, исходя из распределения энергии по спектру, становится возможным оценивать корреляционные свойства сигналов. Чем шире энергетический спектр сигнала, тем меньше интервал корреляции. Соответственно, чем больше интервал корреляции сигнала, тем короче его энергетический спектр.
Во-вторых, соотношения (9)и (10)позволяют экспериментально определить одну из функций по значению другой.
В практических случаях часто удобнее вначале получить автокорреляционную функцию, а затем с помощью прямого преобразования Фурье вычислить энергетический спектр сигнала. Этот приём широко применяется при анализе свойств сигналов в реальном масштабе времени, т.е. без временнó й задержки при его обработке.
Взаимокорреляционная функция двух сигналов
В ряде случаев часто необходимо оценить степень связи между двумя различными аналоговыми сигналам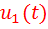и 
и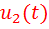 
. Для этих целей используют взаимокорреляционную функцию (ВКФ)
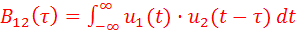................... (11).
При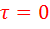 
взаимокорреляционная функция равна так называемой взаимной энергии двух сигналов
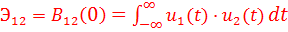................... (12).
Значение ВКФ не меняется, если вместо задержки второго сигнала рассматривать опережение его первым сигналом 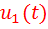. Поэтому выражение (11) можно обобщить следующим образом:
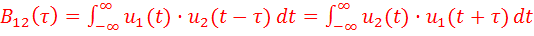....(13)
Необходимо отметить, что в отличие от АКФ взаимокорреляционная функция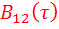 
в общем случае не является чётной и не обязательно максимальной при 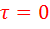, т.е. при отсутствии временнó го сдвига одного из сигналов.
ВКФ является своеобразной мерой «похожести», или коррелированности, двух сигналов при различном их взаимном расположении. Корреляционная функция (КФ) отражает корреляцию сигнала с собственной копией; в этом случае говорят об автокорреляционных свойствах сигнала. Неравенство 
, т.е. непременный максимум КФ при 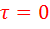в этом контексте может быть объяснено как свидетельство полной корреляции всякого сигнала с самим собой. Уменьшающиеся (иногда немонотонно) значения 
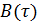характеризуют меру коррелированности, связи сигнала со своей копией при различных 
.
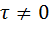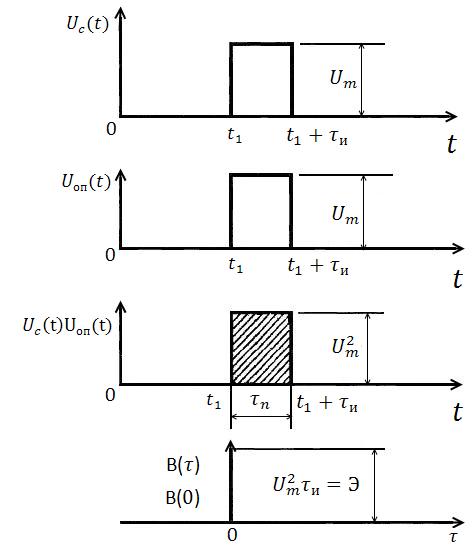
Раскроем смысл корреляционного интеграла и тем самым самого устройства, называемого коррелятором.
Для этого рассмотрим простой пример автокорреляции двух прямоугольных видеоимпульсов амплитудой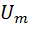 
и длительностью 
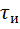(рис.2).
Будем считать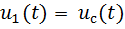 
входным сигналом, а 
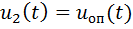– опорным напряжением, с которым будет сравниваться задержанный сигнал. Кроме того, будем полагать, что амплитуды 
.
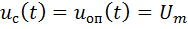Если входной сигнал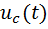 
начинается в момент времени 
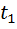(рис.2, а), а опорный 
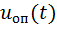запаздывает на 
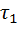, то до момента 
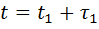, (когда 
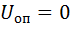) и после 
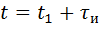(когда 
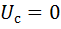), их произведение равно нулю. Только в течение времени 
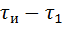, когда каждое напряжение равно 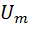, их произведение 
.
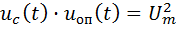Площадь заштрихованного прямоугольника, которая выражает значение корреляционного интеграла для временнό го сдвига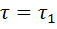 
, равна
.
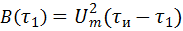На графике корреляционной функции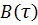 
этот результат представлен вертикальной линией высотой 
, проведенной из точки с координатой 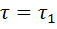на оси абсцисс.
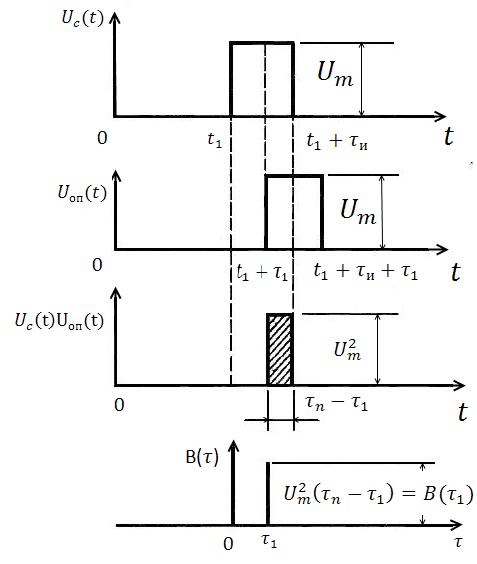
а) б)
в)
Рис.2. К графическому определению автокорреляционной функции
Если 
, т.е. входной и опорный импульсы по всей их длительности совпадают по времени (рис.1, б), то произведение этих сигналов, представленное площадью заштрихованного прямоугольника, равно энергии импульса: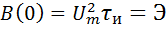 
.
При временнό м сдвиге опорного сигнала в сторону опережения
(
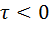) интеграл 
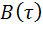уменьшается по сравнению с интегралом 
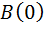, соответствующим 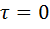. Это иллюстрируется рис.2, в, где 
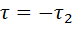и пропорциональное заштрихованной площади выходное напряжение коррелятора 
.
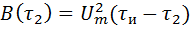Совершив аналогичные операции для всевозможных временн ы х сдвигов (от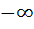 
до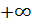 
), получим автокорреляционную функцию 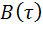прямоугольных импульсов (рис.2).
В данном случае, очевидно, область интегрирования можно ограничить значениями 
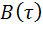. Полученная функция имеет форму равнобедренного треугольника с основанием, равным 
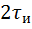, и пиковым значением, равным энергии входного сигнала 
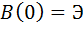(рис.3).
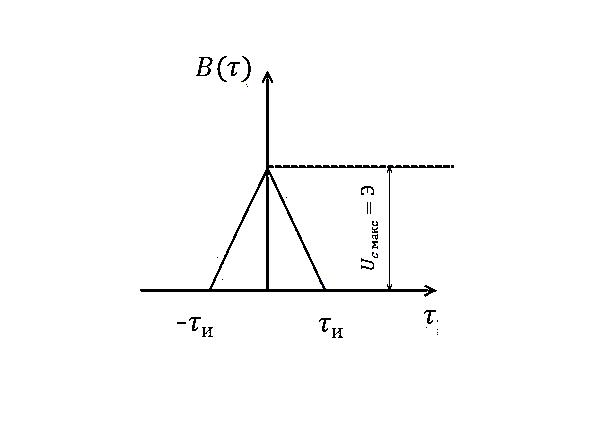
Рис.3. Автокорреляционная функция одиночного
прямоугольного импульса
В импульсной радиолокации широко используются сигналы, представляющие собой пачки из одинаковых по форме импульсов, следующих друг за другом через одинаковый интервал времени, называемый периодом следования зондирующих импульсов.
Рассмотрим пачку из трёх таких прямоугольных видеоимпульсов длительностью и периодом следования 
(рис.4).
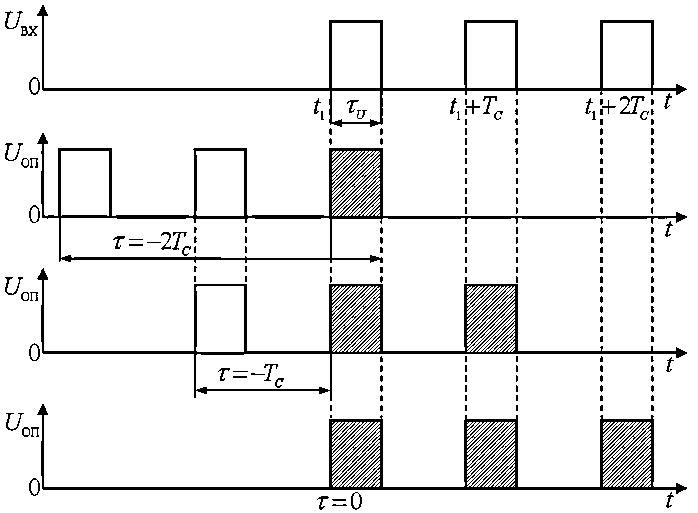
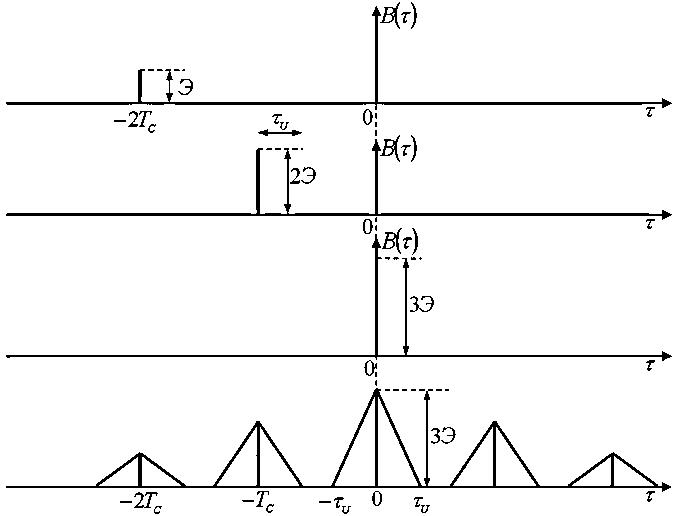
Рис.4. К определению автокорреляционной функции пачки
прямоугольных импульсов
При сдвиге опорного сигнала 
относительно входного сигнала 
на время 
(рис.4, б) лишь один опорный импульс (заштрихованный) полностью совпадает с входным и поэтому 
. Если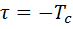 
, то полностью совпадают уже два импульса и 
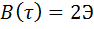, а при 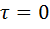– три импульса, что соответствует 
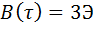и т.д. Ясно, что вблизи этих значений 
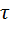корреляционная функция имеет вид равнобедренного треугольника с основанием .
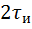В радиотехнике часто вводят удобный для анализа сигналов числовой параметр – интервал корреляции, графически равный ширине основания АКФ. Для данного примера интервал корреляции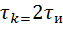 
.
Корреляционная обработка сигналов широко используется в радиолокации. Принцип работы импульсной радиолокационной станции (РЛС) заключается в следующем. Радиопередающее устройство (РПеУ) излучает мощный, короткий зондирующий радиоимпульс в пространство. Мощность излучаемого радиоимпульса может достигать от нескольких сотен киловатт
до 1, 5... 2 мегаватт в импульсе длительностью несколько микросекунд. После излучения зондирующего импульса РЛС переходит в режим приёма отражённого сигнала (эхо-сигнала). Таким образом, РПеУ работает в течение очень короткого времени, после чего следующий зондирующий импульс излучается через 2000... 3000 мкс. На рис.5показана осциллограмма радиолокационного сигнала.
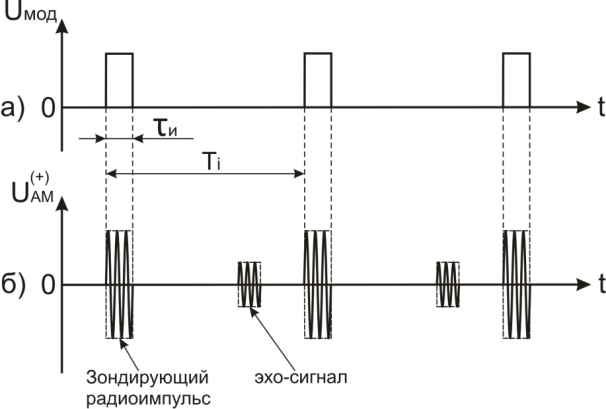
Рис.5. Осциллограмма радиолокационного сигнала
при импульсной модуляции:
а) модулирующие импульсы; б) зондирующие радиосигналы
и эхо-сигналы, отражённые от цели.