
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Указания к выполнению лабораторной работы «Метод Эйлера».
|
|
1. Изучить литературу [1, 9] по вопросам решения ОДУ численными методами.
2. Составить программу решения системы ДУ методом Эйлера, протестировать ее на контрольных примерах.
3. Исходные данные для расчета балки взять по таблице 2 и рис.1.
4. Выполнить расчет для своего варианта и сохранить xls-файл с результатами работы.
5. Распечатать отчет с названием и целью работы, постановкой задачи, текстами программ и результатами расчетов.
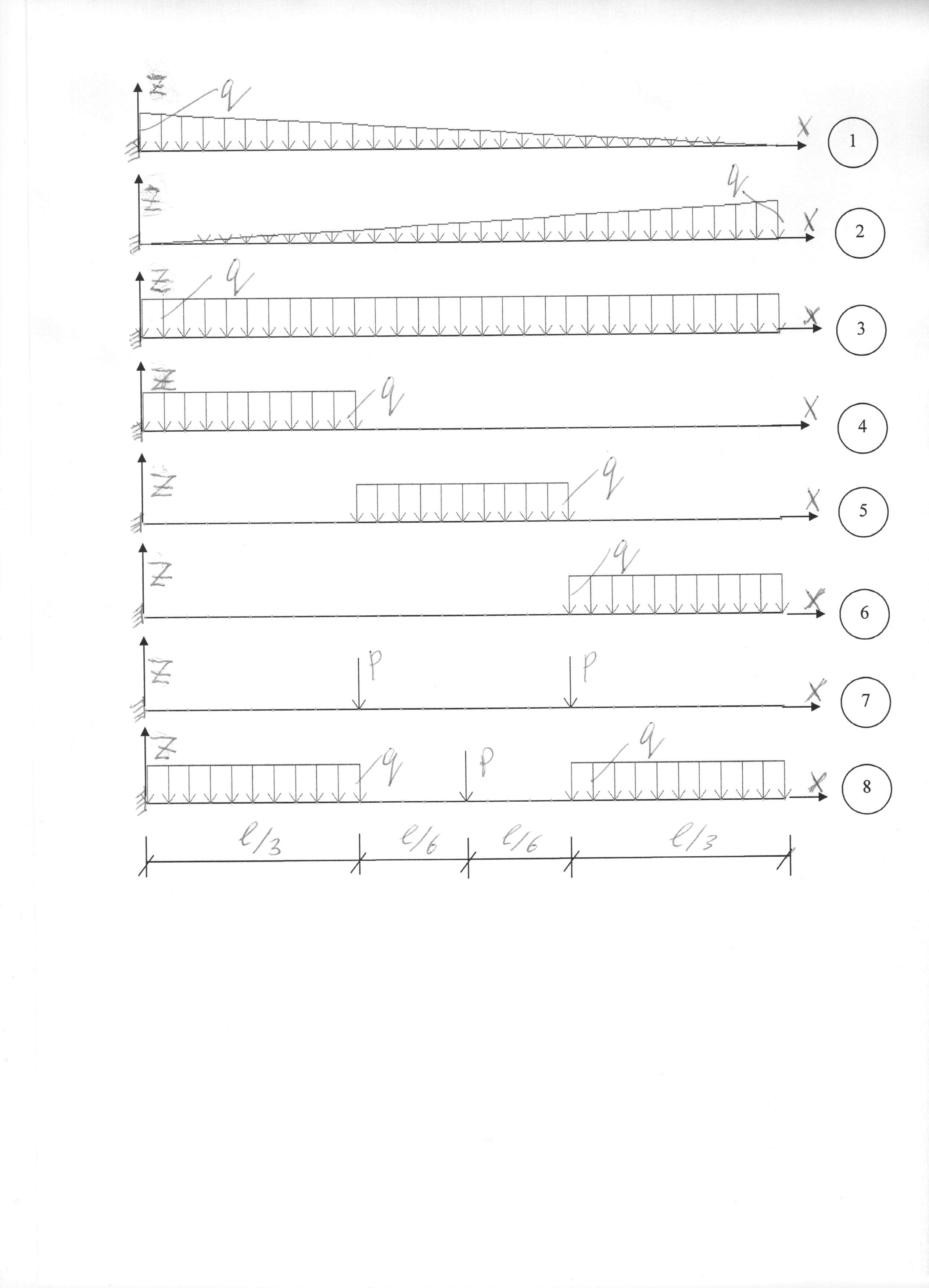
Рисунок 1. Схемы нагружения балок.
Таблица 2
Исходные данные
| Наименование | Номер варианта | |||||||||
| По последней цифре учебного шифра | ||||||||||
| Сосредоточенная сила Р, кН | ||||||||||
| Распределенная нагрузка q, кН/м | ||||||||||
| По предпоследней цифре шифра | ||||||||||
| Пролет балки Ɩ, м | ||||||||||
| № схемы по рис. 1 | ||||||||||
| По третьей с конца цифре шифра | ||||||||||
| Поперечное сечение балки – двутавр № | 50Б1 | 40Б1 | 30Б1 | 60Б1 | 60Б2 | 70Б1 | 30Б2 | 50Б2 | 80Б1 | 35Б2 |
Содержание лабораторной работы «Метод Эйлера».
Тема. Решение дифференциального уравнения изогнутой оси консольной балки методом Эйлера.
Цель. Изучить численные методы решения ОДУ, виды погрешностей при вычислениях, научиться составлять программы для решения систем дифференциальных уравнений.
Задание.
Решить систему дифференциальных уравнений

для заданного варианта балки. Оценить погрешность полученных результатов.
Пример входной информации, текста макроса, расчета и распечатки результатов для балки по варианту № 825.
| Пролет балки Ɩ, (м) | 3.000 |
| интенсивность распределенной нагрузки q, (тс/м) схема №3 | 1.500 |
| изгибная жесткость двутавра 80Б1 EJ (тс х м2) |
Sub eyler()
'Ввод исходных данных из таблиц
l = Cells(2, 2).Value
q = Cells(3, 2).Value
p = Cells(4, 2).Value
EJ = Cells(5, 2).Value
n = Cells(6, 2).Value
'вычисление шага интегрирования
h = l / n
'задание начальных условий
x = 0: Z = 0: fi = 0: i = 0
label:
m = q * (l - x) ^ 2 / 2
'Вывод результатов в ячейки таблицы
Cells(7, 1 + i) = m
Cells(8, 1 + i) = fi
Cells(9, 1 + i) = Z * 1000
Cells(10, 1 + i) = x
i = i + 1: x = x + h
fi = fi + h * m / EJ
Z = Z - h * fi
If i < n + 1 Then GoTo label
End Sub
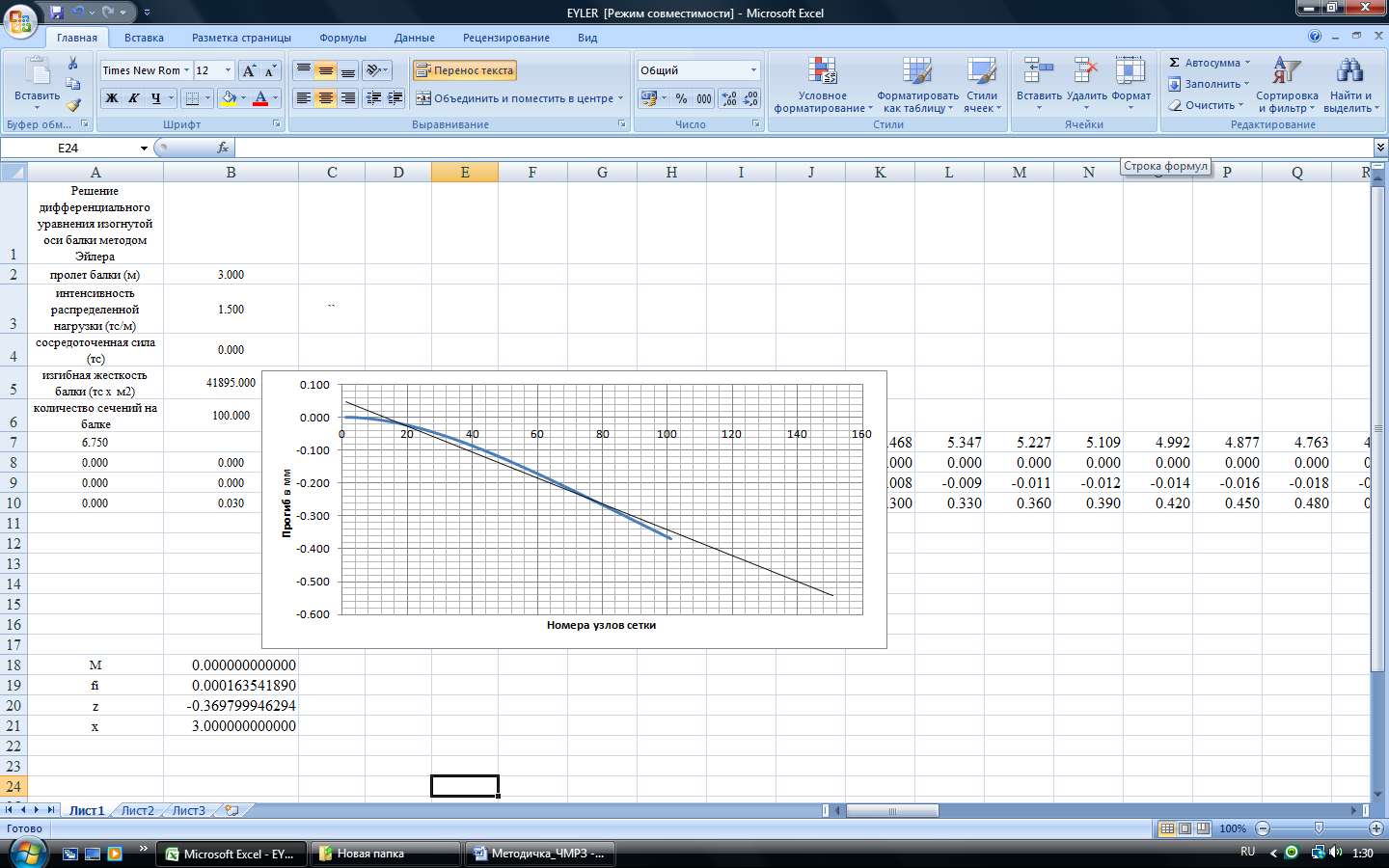
Рисунок 2. Распечатка результатов расчета методом Эйлера.
Проверка значения прогиба на конце балки при х=3 м.
 = 6.75 * 2.25 / 41895= 0.3625 мм.
= 6.75 * 2.25 / 41895= 0.3625 мм.
Вычисленное значение z = 0.3698 мм.
Оценка средней локальной погрешности при n=100 и h= 0.03м составляет

 = 0.03^2*6.75/(2*41895) м = 3.63 * 10^-8 м.
= 0.03^2*6.75/(2*41895) м = 3.63 * 10^-8 м.
Оценка глобальной погрешности за 100 шагов -  3.63 * 10^-6 м = 0.00725 мм.
3.63 * 10^-6 м = 0.00725 мм.