
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача №1. Данная задача является модификацией примера регрессионного анализа, рассмотренного в учебнике по экспериментальной психологии Джеймса Гудвина (С
|
|
Данная задача является модификацией примера регрессионного анализа, рассмотренного в учебнике по экспериментальной психологии Джеймса Гудвина (С. James Goodwin) (2004, с.484, 486-487).
Исследователь пытается выявить взаимосвязь между количеством времени X, бесполезно потраченного студентами, и средним баллом Y их академической успеваемости, который варьируется в пределах от 2, 0 до 5, 0. Под потраченным без пользы временем понимается количество часов определенного соответствующего времяпровождения в неделю (например, занятого просмотром «мыльных» телесериалов). Данные для выборки студентов приведены в табл. 1
Требуется построить линейную регрессионную зависимость среднего балла успеваемости от показателя бесполезно потраченного времени, а также выполнить прогноз успеваемости для значений X, равных 20, 30 и 40 часов.
В ответе к задаче приведите: а) скорректированный процент объясняемой моделью дисперсии отклика, б) оценку уровня значимости регрессии по F-критерию, в) нестандартизованные коэффициенты регрессионного уравнения и оценки их значимости по t-критерию, г) номер наблюдения, имеющего наибольший по модулю остаток, д) прогнозируемые значения отклика.
Таблица 1.
Средний балл успеваемости студентов и показатель бесполезно потраченного ими времени
| № | X | Y | № | X | Y | № | X | Y |
| 1 | 2, 8 | 4 | 3, 9 | 7 | 3, 4 | |||
| 2 | 4, 0 | 5 | 4, 7 | 8 | 4, 4 | |||
| 3 | 3, 2 | 6 | 4, 0 | 9 | 3, 80 |
Решение:
Задачу необходимо при помощи простой регрессионной модели.
Первоначально посмотрим на значение р-уровня значимости по критерию F-Фишера.
Таблица 2.
| Дисперсионный анализb | ||||||
| Модель | Сумма квадратов | ст.св. | Средний квадрат | Щ | Знч. | |
| Регрессия | 2, 210 | 2, 210 | 27, 124 | , 001a | ||
| Остаток | , 570 | , 081 | ||||
| Всего | 2, 780 | |||||
| a. Предикторы: (конст) время потраченное зря | ||||||
| b. Зависимая переменная: успеваемость |
Из таблицы 2 видно, что р-уровень значимости статистически достоверен, поэтому модель может быть содержательно интерпретирована.
Далее посмотрим на значение скорректированного R-квадрата.
Таблица 3.
| Сводка для моделиb | ||||
| Модель | Н | R-квадрат | Скорректи-рованный R-квадрат | Стд. ошибка оценки |
| , 892a | , 795 | , 766 | , 2854 | |
| a. Предикторы: (конст) время потраченное зря | ||||
| b. Зависимая переменная: успеваемость |
Из таблицы 3 видно, что значение КМД (0, 795) достаточно велико, т.е. регрессионная модель объясняет более 79, 5% дисперсии зависимой переменной, и результаты предсказания могут быть приняты во внимание, а скорректированный процент объясняемой моделью дисперсии отклика равен 76, 6%, что приводит к незначительному уменьшению R-квадрат.
Таблица 4.
| Коэффициентыa | ||||||
| Модель | Нестандартизованные коэффициенты | Стандартизованные коэффициенты | t | Знч. | ||
| B | Стд. Ошибка | Бета | ||||
| (Константа) | 5, 521 | , 344 | 16, 057 | , 000 | ||
| Время, потраченное зря | -, 060 | , 011 | -, 892 | -5, 208 | , 001 | |
| a. Зависимая переменная: успеваемость |
Из таблицы 4 видно, что значимость регрессионного коэффициента по критерию t-Стьюдента является достоверной (0, 001). Вклад переменной (Время, потраченное зря) является значимым - 89%, и мы можем включить данный коэффициент в уравнение.
Таблица 5.
| № | Время потраченное зря | Успеваемость | Остаток |
| 2, 8 | -0, 21909 | ||
| 4, 0 | -0, 15075 | ||
| 3, 2 | -0, 47426 | ||
| 3, 9 | 0, 46399 | ||
| 4, 7 | 0, 13232 | ||
| 4, 0 | 0, 02793 | ||
| 3, 4 | 0, 20223 | ||
| 4, 4 | 0, 01101 | ||
| 3, 8 | 0, 00662 |
По полученным остаткам, приведенным в базе «Задача 1», видим, что наибольший по модулю остаток имеет испытуемый №3.
Уравнение регрессии:
У (х)= 5, 521 – 0, 060*(время потраченное зря).
Построим линейную регрессионная зависимость среднего балла успеваемости от показателя бесполезно потраченного времени:
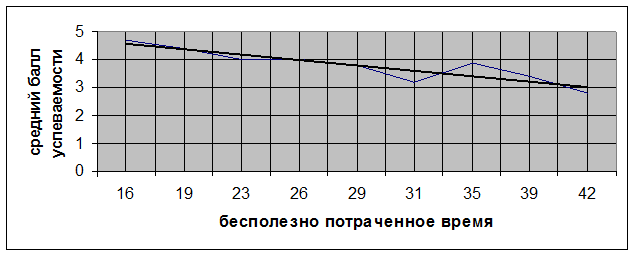
Рис 1. Линейная регрессионная зависимость среднего балла успеваемости от показателя бесполезно потраченного времени.
Прогноз успеваемости для значений X, равных 20, 30 и 40 часов:
У (20) = 5, 521 – 0, 060 * 20 = 4, 321
- студенты, тратящие примерно 20 часов в неделю на бесполезные дела, имеют более высокие оценки зависимой переменной, следовательно, их академическая успеваемость намного выше;
У (30) = 5, 521 – 0, 060 * 30 = 3, 721
- студенты, тратящие без пользы 30 часов в неделю, имеют менее высокие оценки зависимой переменной, соответственно у них наблюдается средняя академическая успеваемость;
У (40) = 5, 521 – 0, 060 * 40 = 3, 121
- учащиеся, которые тратят по 40 часов в неделю без пользы, обладают самыми низкими показателями оценки зависимой переменной и низкой академической успеваемостью.
Таким образом, мы можем сделать вывод о том, что чем большее количество времени тратится студентом на бесполезные дела, тем ниже его академическая успеваемость.
Ответы:
а) скорректированный процент объясняемой моделью дисперсии отклика равен 76, 6%;
б) оценка уровня значимости регрессии по F-критерию равна 28, 5;
в) нестандартизованный коэффициент регрессионного уравнения и оценка его значимости по t-критерию равны -0, 060 и 0, 001 соответственно;
г) наибольший по модулю остаток имеет испытуемый №3;
д) чем большее количество времени тратится студентом на бесполезные дела, тем ниже его академическая успеваемость.
Таблица 6.
| время потраченное зря | Успеваемость | Прогнозируемая оценка зависимой переменной |
| 2, 8 | 3, 01909 | |
| 4, 15075 | ||
| 3, 2 | 3, 67426 | |
| 3, 9 | 3, 43601 | |
| 4, 7 | 4, 56768 | |
| 3, 97207 | ||
| 3, 4 | 3, 19777 | |
| 4, 4 | 4, 38899 | |
| 3, 8 | 3, 79338 |