Числовые характеристики случайных величин

ФР, ЗР и ПВ полностью характеризуют ДСВ и НСВ с вероятностной точки зрения. Однако во многих практических задачах нет надобности в таком полном описании СВ. Часто бывает достаточно указать только отдельные числовые параметры, характеризующие существенные черты распределения вероятностей СВ. Числа, выражающие в сжатой форме характерные свойства распределения СВ, называются числовыми характеристиками (ЧХ) СВ. Наиболее важные среди них математическое ожидание и дисперсия.

Математическое ожидание случайной величины

Рассмотрим отдельно случай ДСВ и НСВ.

Пусть - ДСВ с конечным множеством возможных значени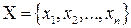й и 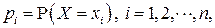- вероятности, с которыми эти значения принимаются, то есть задан закон распределения ДСВ:

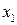
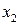
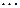
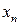
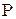
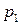
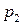
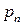
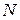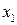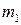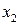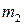Предположим, что над СВ произведено независимых наблюдений, в результате которых значение появилось раз, 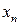- 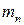раз, …, - раз (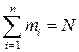). Тогда среднее значение СВ (среднее арифметическое) по результатам 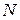наблюдений можно записать в виде:

,

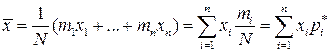где 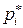- статистическая вероятность (относительная частота) события 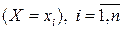. Известно, что 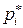при большом 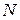близка к истинной вероятности 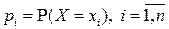. Поэтому, если наблюдения над СВ не производятся, то за ее среднее значение целесообразно принять величину .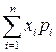

Определение. Математическим ожиданием ДСВ , принимающей значения 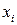с вероятностями 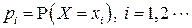, называется величина

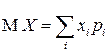, (2.7)

если ряд в правой части абсолютно сходится: .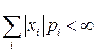

Если ряд в правой части абсолютно расходится, то говорят, что математического ожидания у ДСВ не существует.

Замечание. Естественно, что вопрос о сходимости ряда встает только в случае, когда множество возможных значений ДСВ бесконечно (но счетно). У ДСВ, принимающей конечное число значений, математическое ожидание существует всегда.

Пусть теперь - НСВ с ПВ 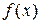. Для определения МО построим следующую ДСВ 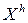, аппроксимирующую НСВ .

Для некоторого 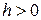рассмотрим точки вида 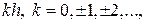на числовой прямой и положим

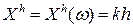, если , .

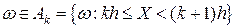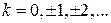СВ 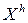принимает значения 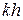с вероятностями

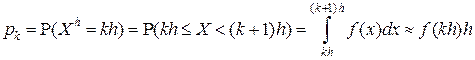
(при малом ), .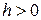

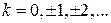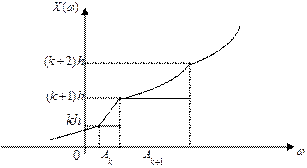
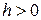
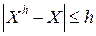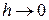При любом и при ДСВ 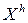все точнее аппроксимирует НСВ . При этом

,

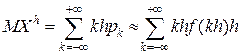если ряд сходится абсолютно. Последняя сумма является интегральной суммой для 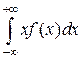, который и следует считать МО НСВ .

Определение. Математическим ожиданием НСВ с плотностью вероятностей 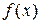называется величина

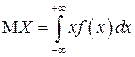, (2.8)

если интеграл в правой части абсолютно сходится: .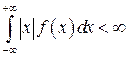

Если интеграл в правой части абсолютно расходится, то говорят, что математического ожидания у НСВ не существует.

Замечание. Формулы (2.7) и (2.8) для МО ДСВ и НСВ можно объединить в одну, записав МО в виде

,

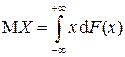где последний интеграл понимается в смысле Римана-Стилтьеса по ФР 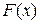(подробнее см. учебник Гнеденко Б.В.).

Механическая интерпретация МО. Если закон распределения интерпретировать как распределение единичной массы вдоль оси абсцисс, то МО – координата центра тяжести (центра масс).

Геометрическая интерпретация МО. МО – среднее значение СВ, около которого группируются другие ее значения (иногда вместо МО СВ говорят среднее СВ ).

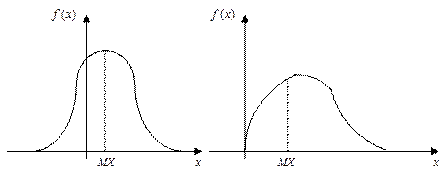
Основная теорема о МО.

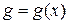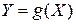Пусть - некоторая СВ, ЗР которой известен (дискретный или непрерывный), - неслучайная функция, область определения которой содержит множество возможных значений СВ . Рассмотрим СВ , являющуюся функцией от СВ .

Как можно найти ?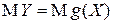

Есть два способа:

а) по ЗР СВ ищется ЗР СВ 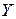и используются стандартные формулы (2.7) и (2.8);

б) с помощью основной теоремы о МО (ОТМО).

Теорема. (ОТМО, теорема о замене переменных, без доказательства)

Пусть - некоторая СВ, ЗР которой известен, СВ 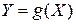является функцией от СВ .

1. Если СВ является дискретной, принимающей значения 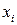с вероятностями 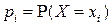, , 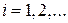и при этом ряд 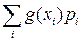абсолютно сходится (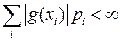), то у СВ 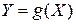существует МО и

.

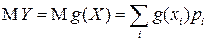2. Если СВ является непрерывной с ПВ 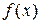и интеграл 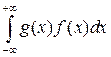абсолютно сходится (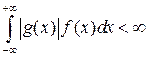), то у СВ 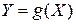существует МО и

.

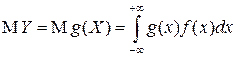Смысл ОТМО: Для нахождения МО СВ 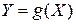, являющейся функцией от СВ , не требуется знать ЗР СВ 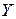, достаточно лишь знать ЗР СВ .

Свойства МО.

1. МО постоянной равно этой постоянной: .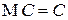

2. Постоянная выносится за знак МО:

.

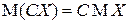▲ Следует из ОТМО при ■.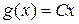

3. МО суммы любых СВ и 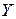равно сумме их МО:

.

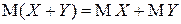▲ Следует из свойств линейности рядов и интегралов ■.

4. Если 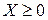, то и .

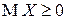Если 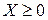и при этом 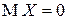, то .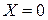

▲ Следует из определения МО для ДСВ и НСВ ■.

Следствие. Если 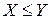, то .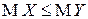

▲ Достаточно применить свойство 4 к СВ ■.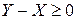

5.

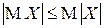
▲ Следует из того, что 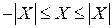для любого 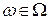. Поэтому в силу свойства 4 МО 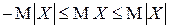, то есть ■.

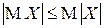Замечание. Свойство 5 справедливо и в более общем виде:

Для любой выпуклой вниз функции 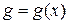справедливо неравенство:

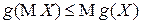(неравенство Йенсена).

Моменты. Дисперсия. Среднее квадратическое отклонение.

Кроме МО, в теории вероятностей используется еще ряд ЧХ различного назначения. Среди них основную роль играют моменты – начальные и центральные.

Определение. Начальным моментом 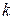-го порядка СВ называется МО 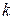-ой степени этой СВ:

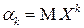, (2.9)

если МО существует.

Как правило, используют начальные моменты 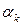целого положительного порядка. В частности, при 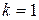имеем 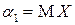, а при .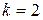

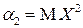Определение. Центральным моментом 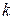-го порядка СВ называется МО 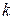-ой степени отклонения этой СВ от ее МО:

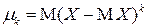, (2.10)

если МО существует.

СВ 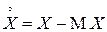называется центрированной СВ (так как 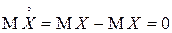). Таким образом, центральный момент – это начальный момент для центрированной СВ:

.

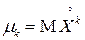Аналогично начальным моментам, центральные моменты 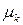обычно используют целого положительного порядка.

В частности, при 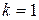имеем 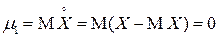для всех СВ.

Особое значение для практики имеет второй центральный момент 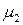, который называется дисперсией СВ и обозначается .

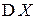Определение. Дисперсией СВ называется МО квадрата отклонения СВ от ее МО:

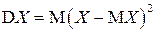. (2.11)

Для дисперсии 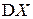справедливо также следующее выражение:

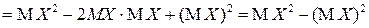
Таким образом, наряду с (2.11)

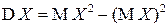. (2.12)

С помощью формулы (2.12) на практике вычислять дисперсию часто бывает проще.

Дисперсия 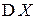характеризует степень разброса (рассеивания) значений СВ относительно ее среднего значения (МО). Чем плотнее группируются значения СВ около МО, тем дисперсия меньше (ср. со смыслом параметра 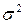в нормальном законе распределения).

Механическая интерпретация дисперсии. Дисперсия представляет собой момент инерции распределения масс относительно центра масс (центра тяжести, МО).

Вычисляются начальные моменты 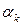по формулам, вытекающим из ОТМО для функции :

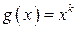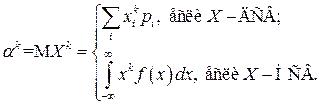
Центральные моменты 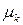вычисляются по формулам, вытекающим из ОТМО для функции :

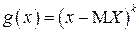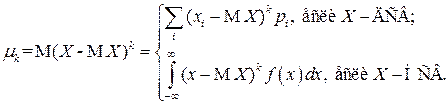
Формулы для вычисления дисперсии 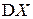вытекают из ОТМО для функции 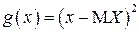(если используется формула (2.11)) или функции 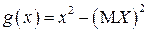(если используется формула (2.12)):

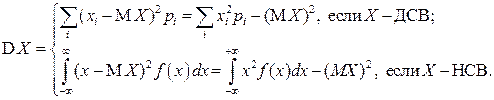
Свойства дисперсии

1. 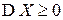, 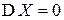тогда и только тогда, когда .

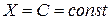▲ Свойство следует из свойства 4 МО ■.

2. Дисперсия не изменяется при прибавлении к СВ константы:

.

▲ ■.

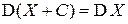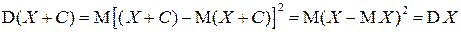3. Константа из-под знака дисперсии выносится с квадратом:

.

▲ ■.

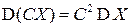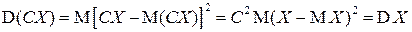Дисперсия имеет размерность квадрата СВ. Характеристикой рассеивания, размерность которой совпадает с размерностью СВ, является среднее квадратическое отклонение 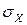(стандартное отклонение), определяемое как корень арифметический из дисперсии:

.

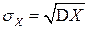С учетом данного определения часто пишут: .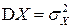

Другие используемые на практике ЧХ.

Величина 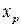, определяемая равенством 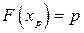, называется
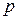- квантилем распределения СВ .

Квантиль 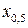называется медианой распределения СВ . Другими словами, медиана – это значение 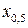на числовой прямой, для которого

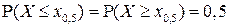
Модой распределения НСВ называется число 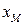, при котором ПВ 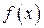достигает максимального значения. Распределения с одной модой называются унимодальными, а распределения с несколькими модами – мультимодальными.

Для симметричных распределений медиана, мода и МО совпадают.