дискретных и непрерывных случайных величин

1. Индикаторная СВ.

Индикаторная СВ имеет вид:

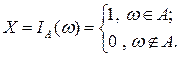
а ее ЗР:

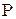
	q	p

где .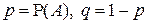

Найдем МО и дисперсию этой СВ.

.

.

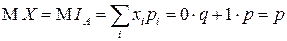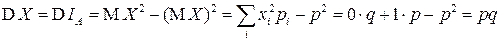Окончательно,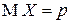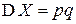

,

2. Биномиальная СВ .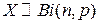

Множество возможных значений биномиальной СВ

,

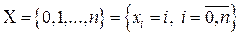а вероятности, с которыми значения принимаются, определяются по формуле Бернулли:

.

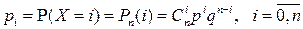Найдем МО СВ .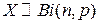

.

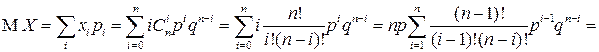
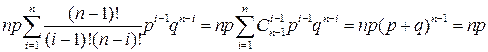Для нахождения дисперсии СВ 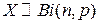вычислим вначале .

.

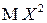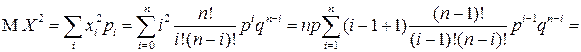
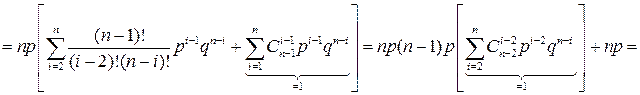
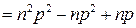Теперь для дисперсии СВ 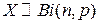получаем выражение:

.

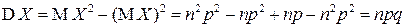Окончательно,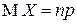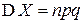

,

3. Геометрическая СВ .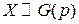

Множество возможных значений геометрической СВ

,

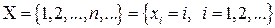а вероятности значений определяются по формуле:

.

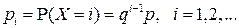Найдем МО СВ .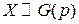

.

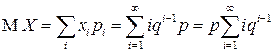Заметим, что ряд 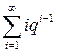представляет собой результат дифференцирования по 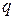геометрической прогрессии 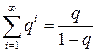. Поэтому

.

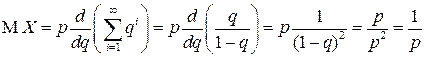Для нахождения дисперсии СВ 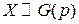вычислим вначале .

.

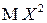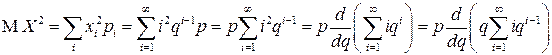Заметим теперь, что при нахождении МО было получено, что 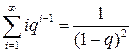. Поэтому

.

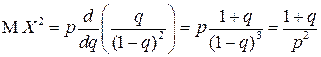Теперь для дисперсии СВ 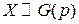получаем выражение:

.

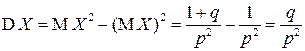Окончательно,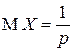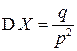

,

4. Пуассоновская СВ .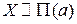

Множество возможных значений пуассоновской СВ

,

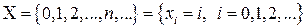а вероятности, с которыми значения принимаются, задаются формулой:

.

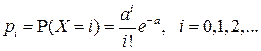Найдем МО СВ .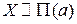

.

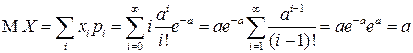Для нахождения дисперсии СВ 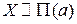вычислим вначале .

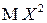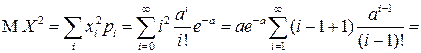
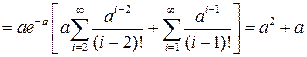
Теперь для дисперсии СВ 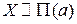получаем выражение:

.

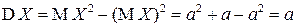Окончательно,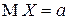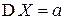

,

5. Равномерная 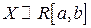СВ .

ПВ СВ , равномерно распределенной на отрезке 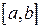, имеет вид:

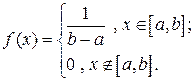
Найдем МО СВ .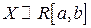

.

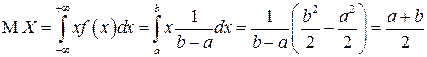Найдем далее .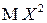

.

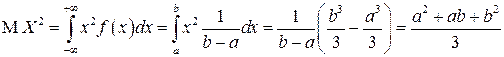Для дисперсии СВ 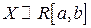получаем выражение:

.

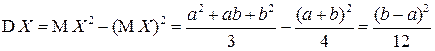Окончательно,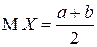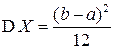

,

6. Показательная (экспоненциальная) СВ .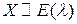

ПВ показательно распределенной СВ имеет вид:

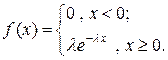
Найдем МО СВ .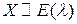

.

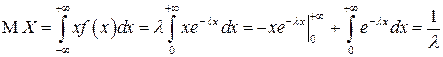Найдем далее .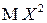

.

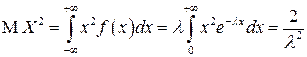Для дисперсии СВ 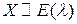получаем выражение:

.

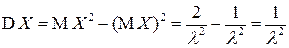Окончательно,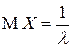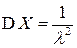

,

7. Нормальная (гауссовская) СВ .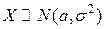

ПВ нормально распределенной с параметрами 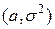СВ имеет вид:

.

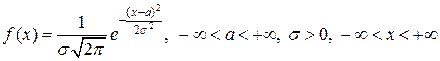Найдем МО СВ .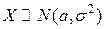

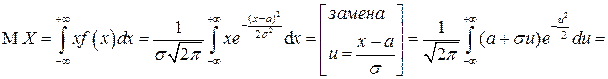
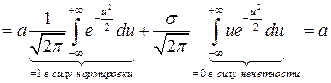
Найдем дисперсию СВ 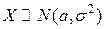(причем в данном случае удобнее пользоваться выражением для дисперсии ).

.

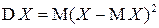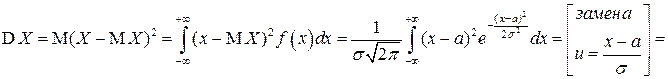
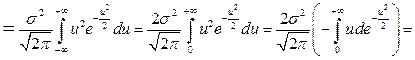
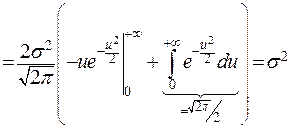Окончательно,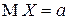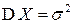

,

8. СВ, имеющая распределение Коши.

СВ , распределенная по закону Коши, имеет ПВ вида:

.

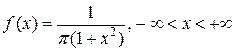Найдем МО этой СВ.

.

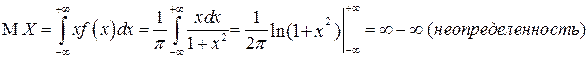В связи с этим проверим выполнения условие существования МО, а именно абсолютную сходимость интеграла .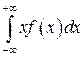

.

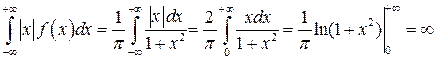Поскольку интеграл 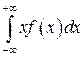абсолютно расходится, то у СВ, распределенной по закону Коши, МО не существует. А, следовательно, у данной СВ не существует дисперсия и другие моменты более высоких порядков.