
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Функция и теорема Эйлера (П)
|
|
10 октября
Функция Эйлера
Определение. Пусть m – натуральное число. Количество чисел, взаимно простых с m и не больших m, обозначается j(m). Функция j(m) называется функцией Эйлера. j(m) равна количеству правильных несократимых дробей со знаменателем m.
1. Докажите, что число j (m) четно при всех m > 2.
2. Найдите сумму всех правильных несократимых дробей со знаменателем n.
3. Пусть p – простое число. а) Найдите j (p); б) Докажите, что j (pn) = pn – 1(p – 1).
4. Докажите, что число a взаимнопросто с m 1 тогда и только тогда, когда взаимнопрост с m 1 остаток r 1 от деления a на m 1.
5. Пусть числа m 1, и m 2 взаимнопросты. Докажите, что j (m 1 m 2)равно количеству пар остатков r 1, r 2 взаимнопростых с m 1 и m 2 соответственно.
6. Докажите, что функция Эйлера мультипликативна: при взаимнопростых a и b j (ab)= j (a) j (b). (Указание: воспользуйтесь китайской теоремой об остатках).
7. Пусть даны n попарно взаимно простых чисел m 1, m 2, …, mn. Докажите, что j (m)= j (m 1)× j (m 2)… j (m n), где m = m 1 m 2… mn,
8. Пусть 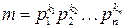 . Докажите:
. Докажите: 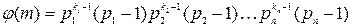 .
.
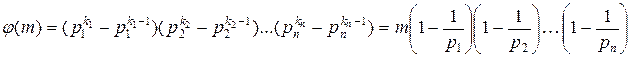
9. Докажите, что j (mk) = mk –1 j (m) для любого m.
10. Решите уравнения: а) 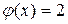 ; б)
; б) 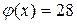 ; в)
; в) 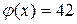 ; г)
; г)  .
.
11. Решите уравнения: а) 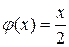 ; б)
; б) 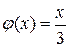 ; в)
; в) 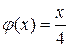 ; г)
; г) 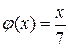 .
.
12. Выпишите все правильные дроби со знаменателем 30 и приведите их все к несократимому виду. Докажите, что: 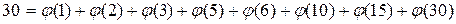 . Докажите, что любое натуральное число равно сумме значений функции Эйлера для всех его делителей? [O1]
. Докажите, что любое натуральное число равно сумме значений функции Эйлера для всех его делителей? [O1]
Теорема Эйлера
Отношение сравнимости по модулю m задает разбиение всех чисел на классы. То есть в один класс объединяются числа, имеющие одинаковые остатки при делении на m. Получившиеся классы называют классами вычетов по модулю m. А целые числа после того, как они разбиты на классы вычетов, зачем-то начинают называть вычетами по модулю m. Совокупность вычетов взятых по одному из каждого класса называют полной системой вычетов (можно, например, взять остатки при делении на m ). Множество классов, образующих полную систему вычетов обозначают 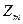 . Если из полной системы вычетов выбрать только вычеты взаимно простые с модулем m, то получится приведенная система вычетов. Множество классов, задающих приведенную систему вычетов, то есть классов, взаимно простых с модулем, обозначают
. Если из полной системы вычетов выбрать только вычеты взаимно простые с модулем m, то получится приведенная система вычетов. Множество классов, задающих приведенную систему вычетов, то есть классов, взаимно простых с модулем, обозначают 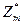 . Таблицы умножения и сложения остатков по заданному модулю m определяют действия над получившимися классами. [o2]
. Таблицы умножения и сложения остатков по заданному модулю m определяют действия над получившимися классами. [o2]
13. Докажите, что, если а взаимно просто с m, то а –тая строка таблицы умножения остатков содержит все элементы Zm, переставленные в другом порядке.
14. Рассмотрите таблицу умножения остатков по модулю m в приведенной системе вычетов 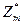 (по аналогии с тем, как мы делали при доказательстве Малой теоремы Ферма) и докажите теорему Эйлера. Для любых натуральных взаимно простых a и m: а j( m )º 1(mod m).
(по аналогии с тем, как мы делали при доказательстве Малой теоремы Ферма) и докажите теорему Эйлера. Для любых натуральных взаимно простых a и m: а j( m )º 1(mod m).
15. Докажите, что при любом нечетном n число 2n! - 1 делится на n.
16. Пусть m – натуральное число не кратное 7. Докажите, существует бесконечно много натуральных n таких, что 7n - 1 делится на m.
17. Существует ли степень тройки, оканчивающаяся на 00001?
18. Найдите все такие целые числа a, для которых число a 10 + 1 делится на 10.
19. na –1 и nb –1 делятся на m. Докажите, что n НОД (a, b) –1 делится на m. (Указание: Рассмотрите наименьшую степень k, такую, что 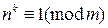 )
)
20. а)Натуральные числа m 1,..., mn попарно взаимно просты. Докажите, что число x = (m 2 m 3... m n) 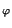 (m1) является решением системы
(m1) является решением системы
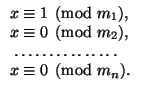
б) Доказательство Китайской теоремы об остатках, приведенное в листке 04 было неконструктивным, то есть мы доказали существование и единственность на отрезке длины m = m 1 m 2… mn числа, обладающего заданным набором остатков по взаимнопростым модулям m 1, m 2, …, mn, однако не привели алгоритма построения этого числа. Придумайте такой алгоритм, используя пункт а).
21. Докажите, что если НОД (a; m) = 1 и b ≡ ax (mod m) и при этом х и j(m) взаимно просты, то всегда найдется такое y < j(m), что by ≡ a (mod m).
[O1]Ну вот просто выписать и посчитать
[o2]Все числа как-бы разложены по ящикам, на которых написаны остатки этих чисел при делении на m. Если мы будем брать произвольное число из ящика с надписью a, и умножать на любое число, взятое из ящика с надписью b, то будем получать каждый раз число из одного и того же ящика, остаток которого сравним с ab.
|