Линейный парный регрессионный анализ

Все существующие связи между признаками классифицируют по степени тесноты, направлению, форме, числу факторов.

По степени тесноты связи делят на статистические и функциональные.

Статистическая связь - это такая связь между при­знаками, при которой для каждого значения признака-фактора Xпризнак-результат 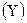может в определенных пределах принимать любые значения с некоторыми вероят­ностями; при этом его статистические (массовые) характе­ристики (например, среднее значение) изменяются по опре­деленному закону.

Статистическая связь обусловлена тем, что:

1) на результативный признак оказывают влияние не только факторы, учтенные в модели (которые мы исследуем), но и неучтенные или неконтролируемые факторы;

2) неизбежностью ошибок измерения значений при­знаков.

Модель статистической связи может быть представле­на в общем виде уравнением: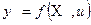

где 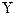- зависимая переменная (предиктор, результативный признак), фактическое значение результативного призна­ка;

Х – независимая переменная (регрессор);

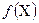- детерминированная составляющая - часть результативного признака, сформировав­шаяся под воздействием учтенных известных факторных признаков;

U – случайная составляющая (случайный остаток).

Противоположной статистической связи является функциональная. Функциональной называется такая связь, когда каждо­му возможному значению признака-фактора 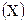соответст­вует одно или несколько строго определенных значений ре­зультативного признака 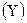. Определение функциональной связи может быть легко обобщено для случая многих при­знаков – 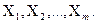Модель функциональной связи в об­щем виде можно представить уравнением:

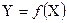
По направлению изменений результативного и фак­торного признаков связи делят на прямые и обратные.

По форме связи (виду функции f) связи делят на пря­молинейные (линейные) и криволинейные (нелинейные).

По количеству факторов в модели связи подразделяют на однофакторные (парные) и многофакторные.

Одним из методов изучения стохастических связей между признаками является регрессионный анализ.

Регрессионный анализ представляет собой установле­ние аналитической зависимости между признаками. Он включает следующие этапы:

1) выбор формы связи (вида аналитического уравнения регрессии);

2) оценка параметров уравнения;

3) оценка качества аналитического уравнения регрес­сии.

Наиболее часто для описания статистической связи признаков используется линейная форма. Внимание к ли­нейной связи объясняется четкой экономической интерпре­тацией ее параметров, ограниченной вариацией переменных и тем, что в большинстве случаев нелинейные формы связи для выполнения расчетов преобразуют (путем логарифми­рования или замены переменных) в линейную форму.

Линейная парная регрессия сводится к нахождению уравнения вида:

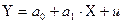
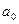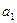где и – параметры уравнения регрессии;

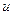- часть результативного признака, сформировавшая­ся под воздействием неконтролируемых или неучтенных факторов, а также ошибок измерения признаков.

Оценка параметров линейной регрессии проводиться по пространственной выборки (Y_i Х_i) . Для получения оценок наиболее часто используют метод наименьших квадратов (МНК).

Метод наименьших квадратов дает наилучшие (эффек­тивные и несмещенные) оценки параметров уравнения рег­рессии. Но только в том случае, если выполняются опреде­ленные предпосылки относительно случайного члена 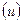и независимой переменной .

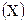МНК позволяет получить такие оценки параметров 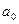и 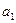, при которых сумма квадратов отклонений фактических значений результативного признака Y – от расчетных (тео­ретических) значений —Ŷ минимальна:

S=Σ (Y-Ŷ)² → min.

Проиллюстрируем суть данного метода графически. Для этого построим точечный график по данным наблюде­ний 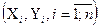в прямоугольной системе координат (та­кой точечный график называют корреляционным полем). Попытаемся подобрать прямую линию, которая ближе всего расположена к точкам корреляционного поля. Согласно ме­тоду наименьших квадратов линия выбирается так, чтобы сумма квадратов расстояний по вертикали между точками корреляционного поля и этой линией была бы минималь­ной.

Y                           Ŷ                         Y                     X                   X

Рисунок 1 - Корреляционное поле зависимости между X и Y.

В случае линейной парной зависимости:

.

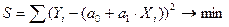Значения 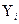и 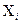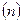нам известны, это данные на­блюдений. В функции S они представляют собой констан­ты. Переменными в данной функции являются искомые оценки параметров – 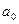и 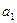. Чтобы найти минимум функции двух переменных необходимо вычислить частные произ­водные данной функции по каждому из параметров и приравнять их к нулю, т.е.

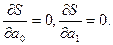
В результате получим систему из 2-ух нормальных линейных уравнений:

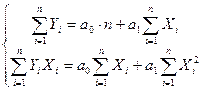или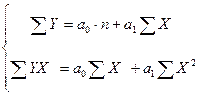

Решая данную систему, найдем искомые оценки пара­метров.

,

,

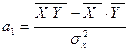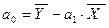где 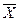, 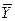и 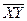- средние значения факторов Х, Y и их произведение.

В системе нормальных уравнений индексы опущены для облегчения запоминания.

Правильность расчета параметров уравнения регрес­сии может быть проверена сравнением сумм Σ Y=Σ Ŷ (при этом возможно некоторое расхождение из-за округления расчетов).

Знак коэффициента регрессии 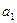указывает направле­ние связи (если 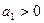, связь прямая, если 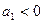, то связь обрат­ная). Величина 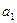показывает, на сколько единиц изменится в среднем признак-результат –Y при изменении признака-фактора – Х на1 единицу своего измерения.

Формально значение параметра 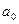- среднее значение Y при Xравном нулю. Если признак-фактор не имеет и не может иметь нулевого значения, то вышеуказанная трак­товка параметра 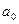не имеет смысла.

Оценка тесноты связи между признаками осуществляется с помощью коэффициента линейной парной корреляции - 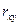. Он может быть рассчитан по формуле: ,

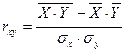Для качественной оценки тесноты связи можно использовать следующую классификацию:

0.1- 0.3- слабая связь

0.3-0.5 – умеренная связь

0.5-0.7- заметная связь

0.7-0.9- тесная связь

0.9-0.99- весьма тесная

где 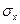- среднее квадратическое отклонение факторного признака, которое определяется по формуле:

.

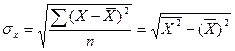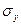- среднее квадратическое отклонение результативного признака, которое определяется по формуле:

.

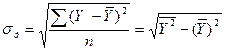Кроме того, коэффициент линейной парной корреляции может быть определен через коэффициент регрессии .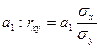

Область допустимых значений линейного коэффици­ента парной корреляции от -1 до +1. Знак коэффициента корреляции указывает направление связи. Если 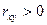, то связь прямая; если 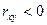, то связь обратная.

Если данный коэффициент по модулю близок к еди­нице, то связь между признаками может быть интерпрети­рована как довольно тесная линейная. Если его модуль ра­вен единице 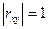, то связь между признаками функцио­нальная линейная. Если признаки X и Y линейно независи­мы, то 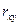близок к 0.

Для оценки качества полученного уравнения регрессии рассчитывают теоретический коэффициент детерминации - 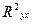. Коэффициент детерминации характеризует долю ва­риации (дисперсии) результативного признака Y, объясняе­мую регрессией (а, следовательно, и фактором Х), в общей вариации (дисперсии) Y. Коэффициент детерминации 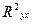принимает значения от 0 до 1. Соответственно величина 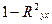характеризует долю дисперсии Y, вызванную влиянием прочих неучтенных в модели факторов и ошибками специ­фикации.

_δ ² Σ (Ŷ - 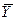)²

R²_yx= ^____ = ^{_____________}

_σ ²_y Σ (Y- 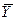)²

где 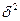- объясненная уравнением регрессии дисперсия Y;

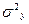- общая (полная) дисперсия Y.

В силу теоремы о сложении дисперсий общая диспер­сия результативного признака равна сумме объясненной уравнением регрессии 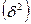и остаточной (необъясненной) 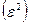дисперсий:

.

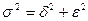Поэтому коэффициент детермина­ции может быть рассчитан через остаточную и общую дис­персии:

ε ² Σ (Y-Ŷ)²

R²=1- ^____ = ^{_____________}

σ ²_y Σ (Y- 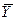)²

где 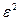- остаточная (необъясненная уравнением регрес­сии) дисперсия Y.

При парной линейной регрессии 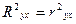.