
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лекция 4 Дискретные и непрерывные случайные величины.
|
|
Раздел IV. Элементы теории вероятностей в социологических исследованиях.
Лекция 4 Дискретные и непрерывные случайные величины.
Цель:
1. Ввести понятие «случайная величина»;
2. Познакомить с дискретной и непрерывной случайной величинами;
3. Изучить законы распределения случайной величины и функцию распределения.
План:
1. Случайные величины и их законы распределения. Примеры случайных величин в социологии.
2. Функция распределения и её свойства.
3. Числовые характеристики дискретных случайных величин.
4. Числовые характеристики непрерывных случайных величин.
1. Случайные величины и их законы распределения.Примеры случайных величин в социологии.
Случайной величиной (СВ) называется величина, которая в зависимости от исхода опыта может принимать то или иное значение, причём заранее не известно какое. Случайные величины обозначаются заглавными латинскими буквами 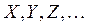 , а их возможные значения – соответствующими строчными буквами
, а их возможные значения – соответствующими строчными буквами 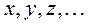
Ранее в литературе обычно предполагалось, что значениями СВ могут быть лишь числа. В настоящее время распространяется более широкий подход, согласно которому значения СВ могут быть достаточно общей природы. Это обстоятельство важно для социологии, где приходится рассматривать такие величины, как, например, пол случайно выбранного человека.
Случайная величина, которая может принимать только отдельные числовые значения, называется дискретной случайной величиной.
Примеры дискретных случайных величин:
1) Оценка, которую студент может получить на экзамене;
2) число несчастных случаев на улицах города Минска;
3) число вызовов, поступивших на телефонную станцию за сутки;
4) число родившихся мальчиков среди десяти новорожденных 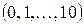 ;
;
Случайные величины, принимающие все значения из некоторого промежутка, называются непрерывными СВ.
1) рост от 150 до 200 см;
2) температура воздуха в случайно выбранный день;
3) скорость самолета в момент выхода на заданную высоту.
4) время ожидания транспорта;
Чтобы задать случайную величину надо указать все значения, которые данная СВ может принимать, но этого не достаточно, надо знать вероятности, с которыми эти значения принимаются.
СВ может быть задана либо с помощью закона распределения, либо с помощью функции распределения.
Дискретная случайная величинам и её закон распределения.
Рассмотрим ДСВ. Все значения ДСВ можно занумеровать: 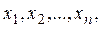 т. е. значений у ДСВ или конечное или счётное множество. При этом каждое из этих значений ДСВ принимает с определённой вероятностью:
т. е. значений у ДСВ или конечное или счётное множество. При этом каждое из этих значений ДСВ принимает с определённой вероятностью:  . Т. е.
. Т. е. 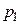 - это вероятность того, что СВ примет значение
- это вероятность того, что СВ примет значение 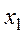 (
(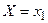 ), …,.
), …,. 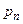 - вероятность того, что СВ примет значение
- вероятность того, что СВ примет значение 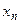 (
(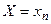 ).
).
Соответствие между значениями 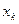 дискретной случайной величины
дискретной случайной величины 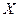 и вероятностями их появления
и вероятностями их появления 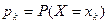 , называется законом распределения случайной величины
, называется законом распределения случайной величины 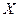 .
.
Простейшей формой задания этого закона распределения является таблица, называемая рядом распределения СВ 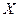 .
.
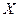
| 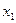
| 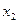
| … | 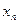
|
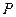
| 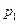
| 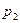
| … | 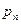
|
Сумма вероятностей всех возможных значений случайной величины равна единице: 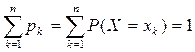 .
.
Рассматриваются также вероятности сочетания значений нескольких СВ. Например, если случайным испытанием является случайный выбор человека из некоторого множества взрослых людей, то вероятность сочетания значений " Мужской" случайной величины " Пол" и значения " Высшее" случайной величины " Образование" есть вероятность того, что выбранный человек окажется мужчиной с высшим образованием.
Для придания ряду распределения более наглядного вида, иногда используют его графическое изображение (называемое многоугольником распределения):
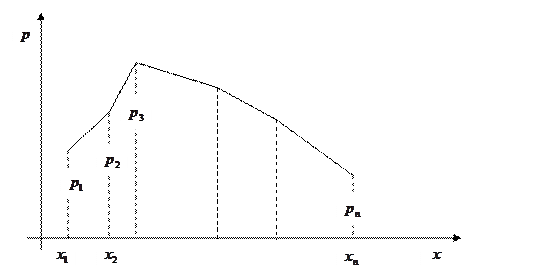
Пример 1. Вероятность того, что стрелок попадет в цель при одном выстреле, равна 0, 6. Стрелок стреляет в цель до первого попадания, имея 3 патрона. Составить ряд распределения СВ Х ‑ числа израсходованных патронов.
| |||
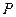
| 0, 6 | 0, 4*0, 6 | 0, 4*0, 4 |
ДСВ можно задать и с помощью функции распределения.
2. Функция распределения и её свойства.
Функция распределения – это функция, значения которой при конкретном значении х есть вероятность события  , т.е.
, т.е.
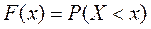 .
.
Функция распределения – самая универсальная характеристика случайной величины. Она существует для всех случайных величин: как дискретных, так и непрерывных. Как числовая функция от числового аргумента х, заданного на всей прямой, функция распределения обладает следующими свойствами:
1. 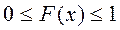 ;
;
2. является неубывающей функцией, т.е. при 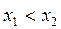
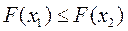 ;
;
3. непрерывна слева, т.е.  ;
;
4. 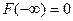 ,
, 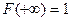 .
.
Функция распределения ДСВ ступенчатая. Точки разрыва ‑ это значения СВ, а скачки разрыва ‑ соответствующие вероятности.
Пример. Вероятность появления события 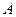 в одном социологическом эксперименте равна 0, 3. Построить функцию распределения случайной величины Х – числа появлений события
в одном социологическом эксперименте равна 0, 3. Построить функцию распределения случайной величины Х – числа появлений события 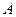 в данном эксперименте.
в данном эксперименте.
Решение. Имеем 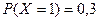 ,
,  . Для функции распределения величины
. Для функции распределения величины 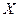 находим:
находим:
1) если 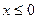 , то
, то 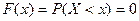 ;
;
2) если 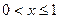 , то
, то 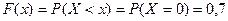 ;
;
3) если  , то
, то 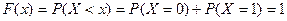 .
.
Следовательно функция распределения имеет вид:
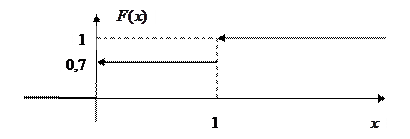
Теорема 1. Вероятность того, что непрерывная случайная величина 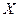 примет какое-либо заданное значения, равна нулю:
примет какое-либо заданное значения, равна нулю: 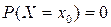 .
.
Теорема 2. Вероятность попадания непрерывной случайной величины в интервал, отрезок и полуинтервал с одними и теми же концами равна разности между значениями функции распределения в правом и левом концах данного промежутка:
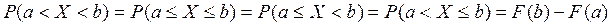 .
.