
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретическая часть. Вопросы для подготовки к зачёту 21.06.2012 г
|
|
Вопросы для подготовки к зачёту 21.06.2012 г. по дисциплине
«Теория вероятностей и математическая статистика» (гр.СОЭ 111 - 2012 год)
Теоретическая часть
1. Цель изучения дисциплины «Теория вероятностей и математическая статистика ». «Понятие предмета «теория вероятностей» и случайного явления (примеры случайных явлений). Какие возможности даёт человечеству изучение случайных явлений. Краткая история возникновения и развития теории вероятностей.
Целью изучения дисциплины является формирование у студентов знаний об основных понятиях теории вероятностей, случайных величинах, их законах распределениях, об основах математической статистики, которые необходимы для методически правильного применения методов теории вероятностей и математической статистики при решении различных финансовых и экономических задач.
Теория вероятностей есть математическая наука, изучающая закономерности в случайных явлениях.
Случайное явление — это такое явление, которое при неоднократном воспроизведении одного и того же опыта протекает каждый раз несколько по-иному.
Примеры:
- Производится стрельба из орудия, установленного под заданным углом к горизонту
- Формирование и обработка плановых и запущенных производственных заказов на предприятии.
- Затраты предприятия на процесс производства производимой продукции в различные интервалы времени (в месяц, в квартал, в течение года).
- Бюджетное и финансовое планирование работы предприятия.
В природе нет ни одного физического явления, в котором не присутствовали бы в той или иной мере элементы случайности. Цель всех вероятностных методов исследования заключается в том, чтобы,, обратиться непосредственно к законам, управляющим массами случайных явлений (процессов). Изучение этих законов целенаправленно влиять на ход случайных явлений. Вероятностный, или статистический, метод в науке является его дополнением, позволяющим глубже анализировать явление с учетом присущих ему элементов случайности.
Краткая историческая справка. Первые работы, представляли собой попытки создания теории азартных игр (Кардано, Гюйгенс, Паскаль, Ферма и другие в XVI—XVII вв.). В работах этих учёных постепенно сформировались понятия «Вероятность», «Событие», «Частота» и др. Эти учёные решали первые задачи теории вероятностей – обшей теории страхования, учёт заболеваемости населения, смертности, статистика насчастных случаев. Следующий этап развития связан с именем Якоба Бернулли (1654—1705). Доказанная имтеорема «Закона больших чисел», была первым теоретическим обоснованием накопленных ранее фактов. «При достаточно большом числе опытов, с практической достоверностью, можно ожидать сколь угодно близкого совпадения частот появления события с его вероятностью». Дальнейшими успехами теория вероятностей обязана Моавру (1667 – 1754 г.г.) - обосновал своеобразный закон, очень часто наблюдаемый в случайных явлениях – так называемый Нормальный закон (иначе закон – Гаусса); П.Лапласу (1749-1827г.г.) - стройное и систематическое изложение основ теории вероятностей; К.Гауссу (1777-1855г.г.) – разработал метод обработки экспериментальных данных («метод наименьших квадратов»); С. Пуассону (1781-1840) – доказал общую форму закона больших чисел, впервые применил теорию вероятностей к задачам стрельбы и др. XVIII и начала XIX века В.Я. Буняковского (1804-1889г.г.) – автор первого курса теории вероятностей на русском языке; П. Л. Чебышева (1821—1894 г.г.) (расширил и обобщил закон больших чисел, ввёл мощный метод моментов различных порядков) и его учеников А.А.Маркова (1856—1922г.г.), А.М.Ляпунова (1857—1918г.г.) В этот период теория вероятностей становится стройной математической наукой. Ее последующее развитие (XIX – XX века) обязано в первую очередь русским и советским математикам: С. Н. Бернштейн; В. И. Романовский (1879-1954г.г.), А. Н. Колмогоров - дал наиболее совершенное аксиоматическое построение теории вероятностей; А. Я.Хинчин (1894 – 1959г.г.) – множество работ в области исследования стационарных случайных процессов, Б. В. Гнеденко – работы в области тории массового облуживания; Н. В. Смирнов – работы в области математической статистики и др.), а также зарубежным математикам - Н.Винер, В. Феллер, Р.Фишер, Д.Нейман и др. – в основном работы в области случайных процессов и математической статистики.
2. Понятие события, примеры событий по степени их возможности появления. Виды случайных событий: совместные и несовместные, попарно совместные и попарно несовместные, полная группа событий – их примеры.
Каждая наука содержит ряд основных понятий, на которых она базируется. Такие основные понятия существуют и в
теории вероятностей. В качестве первого из них введем понятие события. Под «событием» понимается всякий факт,
который в результате опыта может произойти или не произойти. (примеры разных событий). Так или иначе ясно, что
каждое из таких событий обладает той или иной степенью возможности. События называют несовместными, если
появление одного из них исключает появление других событий в одном и том же испытании. Пример 1. Из ящика с
деталями наудачу извлечена деталь. Появление стандартной детали исключает появление нестандартной детали.
События «появилась стандартная деталь» и «появилась нестандартная деталь»—несовместные. Пример 2. Брошена
монета. Появление «герба» исключает появление надписи. События «появился герб» и «появилась надпись» —
несовместные. Несколько событий образуют полную группу, если в результате испытания появится, хотя бы одно из
них. Другими словами, появление хотя бы одного из событий полной группы есть достоверное событие. В частности,
если события, образующие полную группу, попарно несовместны, то в результате испытания появится одно и
только одно из этих событий. Этот частный случай представляет для нас наибольший интерес, поскольку
используется далее. Пример 3. Приобретены два билета денежно-вещевой лотереи. Обязательно произойдет одно и
только одно из следующих событий: «выигрыш выпал на первый.билет и не выпал на второй», «выигрыш не выпал
на первый билет и выпал на второй», «выигрыш выпал на оба билета», «на оба билета выигрыш не выпал». Эти
события образуют полную группу попарно несовместных событий. Пример 4. Стрелок произвел выстрел по цели.
Обязательно произойдет одно из следующих двух событий: попадание, промах. Эти два несовместных события
образуют полную группу. События называют равновозможными, если есть основания считать, что ни одно из них не
является более возможным, чем другое. Пример 5. Появление «герба» и появление надписи при бросании монеты—
равновозможные события. Действительно, предполагается, что монета изготовлена из однородного материала, имеет
правильную цилиндрическую форму и наличие чеканки не оказывает влияния на выпадение той или иной стороны
монеты. Пример 6. Появление того или иного числа очков на брошенной игральной кости—равновозможные события.
Действительно, предполагается, что игральная кость изготовлена из однородного материала, имеет форму
правильного многогранника и наличие очков не оказывает влияния на выпадение любой грани.
3. Виды случайных событий: зависимые и независимые, достоверные и невозможные, равновозможные, противоположные – их примеры.
Достоверным называется событие, которое обязательно произойдет в данном испытании. Например: если в коробке
белые пуговицы, то извлечение из коробки белой пуговицы – событие достоверное. Невозможным называется событие, которое никогда не произойдет в данном испытании. Например: если в коробке белые пуговицы, то извлечение черной пуговицы – событие невозможное. Случайным называется событие, которое может как произойти, так и не произойти в данном испытании. Например, появление герба или реверса при бросании монеты – события случайные. Совместные (совместимые) события – это события, для которых наступление одного из них не исключает возможности наступления других в данном испытании, т.е. они могут появиться вместе. Несовместные (несовместимые) события - это события, для которых наступления одного из них исключает наступление других в одном и том же испытании, т.е. они не могут появиться вместе. Например, получение студентом на экзамене по одной дисциплине оценок “отлично”, “хорошо”, “удовлетворительно” – события несовместные, а получение этих же оценок на экзамене по трем дисциплинам – события совместные. Равновозможные события - это события, для которых ни одно из них не является более возможным, чем другие, в данном испытании. Единственно возможные события – это события, если при испытании обязательно наступит хотя бы одно из них. Например, события, состоящие в том, что в семье из двух детей: 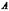 - “два мальчика”,
- “два мальчика”, 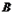 - “две девочки”,
- “две девочки”, 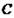 - “один мальчик и одна девочка” – являются единственно возможными. Несколько событий образуют полную группу, если они являются единственно возможными и несовместными исходами испытания. Это означает, что в результате испытания обязательно должно произойти одно и только одно из этих событий. Два события, образующие полную группу, называются противоположными событиями. Событие, противоположное событию
- “один мальчик и одна девочка” – являются единственно возможными. Несколько событий образуют полную группу, если они являются единственно возможными и несовместными исходами испытания. Это означает, что в результате испытания обязательно должно произойти одно и только одно из этих событий. Два события, образующие полную группу, называются противоположными событиями. Событие, противоположное событию 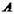 , обозначают
, обозначают 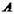 .
.
4. Понятие вероятности события. Понятие элементарного и благоприятствующего события. Классическое определение вероятности, формула её вычисления, свойства данного определения вероятности и их доказательство. Основные недостатки классического определения вероятности. Аксиомы, предложенные академиком А.Н. Колмогоровым, в отношении определений случайного события и его вероятности.
Чтобы количественно сравнивать между собой события по степени их возможности, очевидно, нужно с каждым событием связать определенное число, которое тем больше, чем более возможно событие. Такое число и назовают вероятностью события.Вероятность события есть численная мера степени объективной возможности этого события. На основании опыта мы считаем более вероятными те события, которые происходят чаще; менее вероятными — те события, которые происходят реже; мало вероятными—те, которые почти никогда не происходят. Таким образом, понятие вероятности события в самой своей основе связано с опытным, практическим понятием частоты события. Вероятность—одно из основных понятий теории вероятностей. Существует несколько определений этого понятия. Приведем определение, которое называют классическим. Вероятность есть число, характеризующее степень возможности появления события.
 | |||||
 | |||||
 |
Отношение числа благоприятствующих событию А элементарных исходовк общему числу называют вероятностью события А и обозначают через 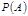 . (классическое) Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.
. (классическое) Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу. 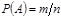 где m—число элементарных исходов, благоприятствующих А; п— число всех возможных элементарных исходов испытания. Элементарные исходы несовместны, равновозможны и образуют полную группу. Из классического определения вероятности вытекают следующие её свойства: Свойство 1. Вероятность достоверного события равна единице.В этом случае m = n, следовательно
где m—число элементарных исходов, благоприятствующих А; п— число всех возможных элементарных исходов испытания. Элементарные исходы несовместны, равновозможны и образуют полную группу. Из классического определения вероятности вытекают следующие её свойства: Свойство 1. Вероятность достоверного события равна единице.В этом случае m = n, следовательно 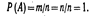 Свойство 2. Вероятность невозможного события равна нулю.В этом случае m = 0, следовательно,
Свойство 2. Вероятность невозможного события равна нулю.В этом случае m = 0, следовательно, 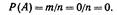 Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.В этом случае
Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.В этом случае 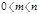 , значит,
, значит,  , следовательно:
, следовательно: 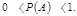 Итак, вероятность любого события удовлетворяет двойному неравенству
Итак, вероятность любого события удовлетворяет двойному неравенству 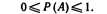 Замечание 1. Современные строгие курсы теории вероятностей построены на теоретико-множественной основе. Пусть в результате испытания наступает одно и только одно из
Замечание 1. Современные строгие курсы теории вероятностей построены на теоретико-множественной основе. Пусть в результате испытания наступает одно и только одно из
 | |||
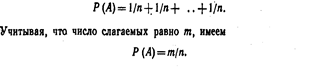 | |||
Получено классическое определение вероятности. Замечание 2. Построение логически полноценной теории вероятностей основано на аксиоматическом определении случайного события и его вероятности. В системе аксиом, предложенной А. Н. Колмогоровым, неопределяемыми понятиями являются элементарное событие и вероятность. Приведем аксиомы, определяющие вероятность: 1. Каждому событию А поставлено в соответствие неотрицательное действительное число Р (А). Это число называется вероятностью события А. 2. Вероятность достоверного события равна единице: 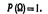 3. Вероятность наступления хотя бы одного из попарно несовместных событий равна сумме вероятностей этих событий. Исходя из этих аксиом, свойства вероятностей и зависимости между ними выводят в качестве теорем. ??? Классическое определение вероятности предполагает, что число элементарных исходов испытания конечно. На практике же весьма часто встречаются испытания, число возможных исходов которых бесконечно. В таких случаях классическое определение неприменимо. Уже это обстоятельство указывает на ограниченность Классического определения. Наиболее слабая сторона классического определения состоит в том, что очень часто невозможно представить результат испытания в виде совокупности элементарных событий. Еще труднее указать основания, позволяющие считать элементарные события равновозможными. Обычно о равновозможности элементарных исходов испытания говорят из соображений симметрии. Так, например, предполагают, что игральная кость имеет форму правильного многогранника (куба) и изготовлена из однородного материала. Однако задачи, в которых можно исходить из соображений симметрии, на практике встречаются весьма редко.
3. Вероятность наступления хотя бы одного из попарно несовместных событий равна сумме вероятностей этих событий. Исходя из этих аксиом, свойства вероятностей и зависимости между ними выводят в качестве теорем. ??? Классическое определение вероятности предполагает, что число элементарных исходов испытания конечно. На практике же весьма часто встречаются испытания, число возможных исходов которых бесконечно. В таких случаях классическое определение неприменимо. Уже это обстоятельство указывает на ограниченность Классического определения. Наиболее слабая сторона классического определения состоит в том, что очень часто невозможно представить результат испытания в виде совокупности элементарных событий. Еще труднее указать основания, позволяющие считать элементарные события равновозможными. Обычно о равновозможности элементарных исходов испытания говорят из соображений симметрии. Так, например, предполагают, что игральная кость имеет форму правильного многогранника (куба) и изготовлена из однородного материала. Однако задачи, в которых можно исходить из соображений симметрии, на практике встречаются весьма редко.
5. Понятие относительной частоты события и особенность её по отношению к вероятности, формула её вычисления, основное свойство относительной частоты события, примеры вычисления относительных частот. Статистическое определение вероятности, его недостаток и свойства статистической вероятности.
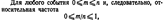 Относительная частота принадлежит к основным понятиям теории вероятностей. Относительной частотой события называют отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний. Таким образом, относительная частота события А определяется формулой
Относительная частота принадлежит к основным понятиям теории вероятностей. Относительной частотой события называют отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний. Таким образом, относительная частота события А определяется формулой 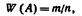 где т — число появлений события, п — общее число испытаний.Определение вероятности не требует, чтобы испытания производились в действительности; определение же относительной частоты предполагает, что испытания были произведены фактически. Вероятность вычисляют до опыта, а относительную частоту—после опыта. Пример I. Отдел технического контроля обнаружил 3 нестандартных детали в партии из 80 случайно отобранных деталей. Относительная частота появления нестандартных деталей
где т — число появлений события, п — общее число испытаний.Определение вероятности не требует, чтобы испытания производились в действительности; определение же относительной частоты предполагает, что испытания были произведены фактически. Вероятность вычисляют до опыта, а относительную частоту—после опыта. Пример I. Отдел технического контроля обнаружил 3 нестандартных детали в партии из 80 случайно отобранных деталей. Относительная частота появления нестандартных деталей 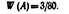 Пример 2. По цели произвели 24 выстрела, причем было зарегистрировано 19 попаданий. Относительная частота поражения цели:
Пример 2. По цели произвели 24 выстрела, причем было зарегистрировано 19 попаданий. Относительная частота поражения цели: 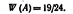 Длительные наблюдения показали, что если в одинаковых условиях производят опыты, в каждом из которых число испытаний достаточно велико, то относительная частота обнаруживает свойство устойчивости - в различных опытах относительная частота изменяется мало (тем меньше, чем больше произведено испытаний), колеблясь около некоторого постоянного числа. Это постоянное число есть вероятность появления события. Пример 3. По данным шведской статистики, относительная частота рождения девочек за 1935 г. по месяцам характеризуется следующими числами (числа расположены в порядке следования месяцев, начиная с января): 0, 486; 0, 489; 0, 490; 0.471; 0, 478; 0, 482; 0, 462; 0, 484; 0, 485; 0, 491; 0.482; 0, 473 Относительная частота колеблется около числа 0, 482, которое можно принять за приближенное значение вероятности рождения девочек. Статистические данные различных стран дают примерно то же значение относительной частоты. Ограниченность классического определения вероятности. Статистическая вероятность. Наряду с классическим определением вероятности используют и другие определения, в частности статистическое определение вероятности: в качестве статистической вероятности события принимают относительную частоту или число, близкое к ней. Например, если в результате достаточно большого числа испытаний оказалось, что относительная частота весьма близка к числу 0, 4, то это число можно принять за статистическую вероятность события. Легко проверить, что свойства вероятности, вытекающие из классического определения, сохраняются и при статистическом определении вероятности. 1).Действительно, если событие достоверно, то т = п и относительная частота
Длительные наблюдения показали, что если в одинаковых условиях производят опыты, в каждом из которых число испытаний достаточно велико, то относительная частота обнаруживает свойство устойчивости - в различных опытах относительная частота изменяется мало (тем меньше, чем больше произведено испытаний), колеблясь около некоторого постоянного числа. Это постоянное число есть вероятность появления события. Пример 3. По данным шведской статистики, относительная частота рождения девочек за 1935 г. по месяцам характеризуется следующими числами (числа расположены в порядке следования месяцев, начиная с января): 0, 486; 0, 489; 0, 490; 0.471; 0, 478; 0, 482; 0, 462; 0, 484; 0, 485; 0, 491; 0.482; 0, 473 Относительная частота колеблется около числа 0, 482, которое можно принять за приближенное значение вероятности рождения девочек. Статистические данные различных стран дают примерно то же значение относительной частоты. Ограниченность классического определения вероятности. Статистическая вероятность. Наряду с классическим определением вероятности используют и другие определения, в частности статистическое определение вероятности: в качестве статистической вероятности события принимают относительную частоту или число, близкое к ней. Например, если в результате достаточно большого числа испытаний оказалось, что относительная частота весьма близка к числу 0, 4, то это число можно принять за статистическую вероятность события. Легко проверить, что свойства вероятности, вытекающие из классического определения, сохраняются и при статистическом определении вероятности. 1).Действительно, если событие достоверно, то т = п и относительная частота 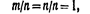 т. е. статистическая вероятность достоверного события (так же как и в случае классического определения) равна единице.2). Если событие невозможно, то m = 0 и, следовательно, относительная частота0/0=0, т. е. статистическая вероятность невозможного события равна нулю.3). т. е. статистическая вероятность любого события заключена между нулем и единицей. Для существования статистической вероятности события А требуется: а) возможность, хотя бы принципиально, производить неограниченное число испытаний, в каждом из которых событие А наступает или не наступает; б) устойчивость относительных частот появления А в различных сериях достаточно большого числа испытаний. Недостатком статистического определения является - неоднозначность статистической вероятности. Так, в приведенном примере, в качестве вероятности события можно принять не только 0.4, но и 0, 39; 0, 41 и т. д.
т. е. статистическая вероятность достоверного события (так же как и в случае классического определения) равна единице.2). Если событие невозможно, то m = 0 и, следовательно, относительная частота0/0=0, т. е. статистическая вероятность невозможного события равна нулю.3). т. е. статистическая вероятность любого события заключена между нулем и единицей. Для существования статистической вероятности события А требуется: а) возможность, хотя бы принципиально, производить неограниченное число испытаний, в каждом из которых событие А наступает или не наступает; б) устойчивость относительных частот появления А в различных сериях достаточно большого числа испытаний. Недостатком статистического определения является - неоднозначность статистической вероятности. Так, в приведенном примере, в качестве вероятности события можно принять не только 0.4, но и 0, 39; 0, 41 и т. д.
6. Понятие комбинаторики, её основные определения и формулы, примеры основных понятий комбинаторики. Правила суммы и произведения комбинаторики.
Комбинаторика раздел математики, который изучает количества комбинаций, подчиненных определенным условиям, которые можно составить из элементов, безразлично какой природы, заданного конечного множества. При непосредственном вычислении вероятностей часто используют формулы комбинаторики. Перестановками (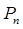 )
)  называют комбинации, состоящие из одних и тех же п различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок:
называют комбинации, состоящие из одних и тех же п различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок:  где n! =1
где n! =1 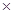 2
2 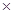 3
3 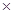 ..
.. 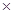 п. Заметим, что удобно рассматривать 0!, полагая, по определению, 0! =1. Пример 1. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только один раз? Решение. Искомое число трехзначных чисел Р3=3! =1
п. Заметим, что удобно рассматривать 0!, полагая, по определению, 0! =1. Пример 1. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только один раз? Решение. Искомое число трехзначных чисел Р3=3! =1 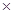 2
2 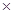 3=6. Размещениями (
3=6. Размещениями (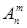 )называют комбинации, составленные из n различных элементов по т элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений:
)называют комбинации, составленные из n различных элементов по т элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений: 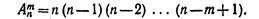 Пример 2. Сколько можно составить сигналов из 6 флажков различного цвета, взятых no 2? Решение. Искомое число сигналов
Пример 2. Сколько можно составить сигналов из 6 флажков различного цвета, взятых no 2? Решение. Искомое число сигналов 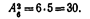 Сочетаниями (
Сочетаниями (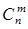 ) называют комбинации, составленные из «n» различных элементов по «т» элементов, которые отличаются хотя бы одним элементом. Число сочетаний:
) называют комбинации, составленные из «n» различных элементов по «т» элементов, которые отличаются хотя бы одним элементом. Число сочетаний: 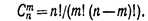 Пример 3. Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей? Решение. Искомое число способов
Пример 3. Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей? Решение. Искомое число способов 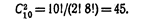 Подчеркнем, что числа размещений, перестановок и сочетаний связаны равенством
Подчеркнем, что числа размещений, перестановок и сочетаний связаны равенством 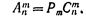 Замечание. Выше предполагалось, что все n элементов различны. Если же некоторые элементы повторяются, то в этом случае комбинации с повторениями вычисляют во другим формулам.
Замечание. Выше предполагалось, что все n элементов различны. Если же некоторые элементы повторяются, то в этом случае комбинации с повторениями вычисляют во другим формулам. 
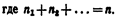 При решении задач комбинаторики используют следующие правила: Правило суммы. Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m+n способами. Правило произведения. Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана тп способами.
При решении задач комбинаторики используют следующие правила: Правило суммы. Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m+n способами. Правило произведения. Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана тп способами.
7. Понятие суммы и произведения двух и нескольких событий, иллюстрация суммы и произведения двух и трёх несовместных событий. Пример записи сложного события с помощью операций суммы и произведения простых событий. Четыре важных следствия понятий суммы и произведения событий, их иллюстрация.
8. Теорема сложения вероятностей для двух несовместных событий, её условия и доказательство, следствие для нескольких попарно несовместных событий – его доказательство. Примеры применения данной теоремы для двух событий.
9. Теорема сложения вероятностей событий, образующих полную группу – её условия и доказательство, пример её применения.
10. Понятие противоположных событий, теорема сложения вероятностей противоположных событий, её доказательство, два замечания данной теоремы. Примеры применения данной теоремы и её замечаний.
11. Принцип практической невозможности маловероятных событий, понятие уровня значимости, интервалы их значений, следствие данного принципа.
12. Понятие зависимого и независимого события, их примеры. Понятия условной вероятности события, варианты её записи, примеры её вычисления. Общая формула вычисления условной вероятности.
Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет.Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.Рассмотрим примеры. 1) Опыт состоит в бросании двух монет; рассматриваются события: А — появление герба на первой монете, В — появление герба на второй монете.В данном случае вероятность события А не зависит от того, произошло событие В или нет; событие А н е з а в и с и м о от события В. 2) В урне два белых шара и один черный; два лица вынимают из урны по одному шару; рассматриваются события: А—появление белого шара у 1-го лица, В — появление белого шара у 2-го лица. Вероятность события А до того, как известно что-либо о событии В, равна 2/3. Если стало известно, что событие В произошло, то вероятность события А становится равной 1/2, из чего заключаем, что событие А зависит от события В. Вероятность события вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обозначается Р(А/В) или РВ(А). Для условий последнего примера 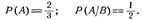 Условие независимости события А от события В можно записать в виде:
Условие независимости события А от события В можно записать в виде: 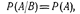 а условие зависимости—в виде:
а условие зависимости—в виде: 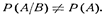 Другое определение условной вероятности: Условной вероятностью РА(В) называют вероятность события В, вычисленную в предположении, что событие А уже наступило. Пример. В урне 3 белых и 3 черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно. Найти вероятность появления белого шара при втором испытании (событие В), если при первом испытании был извлечен черный шар (событие А). Решение. После первого испытания в урне осталось 5 шаров, из них 3 белых. Искомая условная вероятность
Другое определение условной вероятности: Условной вероятностью РА(В) называют вероятность события В, вычисленную в предположении, что событие А уже наступило. Пример. В урне 3 белых и 3 черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно. Найти вероятность появления белого шара при втором испытании (событие В), если при первом испытании был извлечен черный шар (событие А). Решение. После первого испытания в урне осталось 5 шаров, из них 3 белых. Искомая условная вероятность
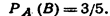 Этот же результат можно получить по формуле
Этот же результат можно получить по формуле
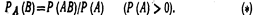 Действительно, вероятность появления белого шара при первом испытании
Действительно, вероятность появления белого шара при первом испытании 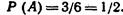
 |
Искомая условная вероятность 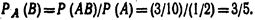 (*) Общее определение условной вероятности: Условная вероятность события В при условии, что событие А уже наступило, по определению, равнаРА (В)=Р(АВ)/Р(А) (Р(А)> 0).
(*) Общее определение условной вероятности: Условная вероятность события В при условии, что событие А уже наступило, по определению, равнаРА (В)=Р(АВ)/Р(А) (Р(А)> 0).
13. Теорема умножения для двух зависимых событий, её условия и доказательство, следствие данной теоремы для нескольких событий, примеры применения данной теоремы и её следствия.
Рассмотрим два события: А и В; пусть вероятности Р(А) и РА(В) известны. Как найти вероятность совмещения этих событий. Теорема. Вероятность совместного появления двух событии равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило: 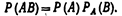 Доказательство. По определению условной вероятности.
Доказательство. По определению условной вероятности. 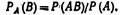
Отсюда 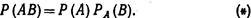 Замечание. Применив формулу (*) к событию ВА, получим
Замечание. Применив формулу (*) к событию ВА, получим
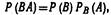 или, поскольку событие ВА не отличается АВ,
или, поскольку событие ВА не отличается АВ, 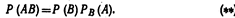
Сравнивая формулы (*) и (**),  Следствие. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились:
Следствие. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились: 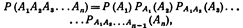

порядок, в котором расположены события, может быть выбран любым, т.е. безразлично какое событие считать первым, вторым и т. д. Пример 1. У сборщика имеется 3 конусных и 7 эллиптических валиков. Сборщик взял один валик, а затем второй. Найти вероятность того, что первый из взятых валиков—конусный, а второй — эллиптический.Решение. Вероятность того, что первый валик окажется конусным событие А), 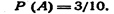
Вероятность того, что второй валик окажется эллиптическим (событие в), 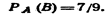 искомая вероятность
искомая вероятность
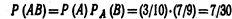
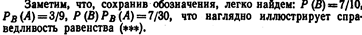
14. Понятие независимого события, теорема умножения для двух независимых событий, её условия и доказательство. Понятие попарно независимых и независимых в совокупности событий. Следствие из теоремы умножения для нескольких событий, независимых в совокупности, его доказательство, замечание следствия для нескольких противоположных событий. Примеры применения данной теоремы и её следствия.
Пусть вероятность события В не зависит от появления события А.
Событие В называют независимым от события А если условная вероятность события В равна его безусловной вероятности:  Используя
Используя 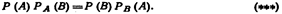 получим
получим 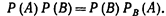 Отсюда
Отсюда 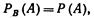 Другими словами, событие А не зависит от события В. Итак, если событие В не зависит от события А, то и событие А не зависит от события В; т.е. свойство независимости событий взаимно. Для независимых событий теорема умножения
Другими словами, событие А не зависит от события В. Итак, если событие В не зависит от события А, то и событие А не зависит от события В; т.е. свойство независимости событий взаимно. Для независимых событий теорема умножения 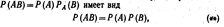
т. е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий. Два события называют независимыми(**), если вероятность их совмещения равна произведению вероятностей этих событий; в противном случае события называют зависимыми.. На практике о независимости событий заключают по смыслу задачи. Пример 1. Найти вероятность совместного поражения цели двумя орудиями, если вероятность поражения цели первым орудием (событие А) равна 0, 8, а вторым (событие В)— 0, 7.Решение. События А и В независимые, поэтому, по теореме умножения, искомая вероятность
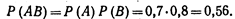

Следовательно, 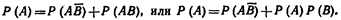
Отсюда 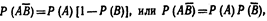
т. е. события А и В независимы.  Несколько событий называют попарно независимыми» если каждые два из них независимы. Например, события А, В, С попарно независимы, если независимы события А и В, А и С, В и С. Для того чтобы обобщить теорему умножения на несколько событий, введем понятие независимости событий в совокупности. Несколько событий называют независимыми в совокупности (или просто независимыми), если независимы каждые два из них и независимы каждое событие и все возможные произведения остальных. Условная вероятность появления любого события из них равна, его безусловной вероятности. если несколько событий независимы попарно, то отсюда еще не следует их независимость в совокупности требование независимости событий в совокупности сильнее требования их попарной независимости. Поясним сказанное на примере. Пусть в урне имеется 4 шара, окрашенные: один—в красный цвет (А), один— в синий цвет (В), один—в черный цвет (С) и один—во все эти три цвета (АВС). Чему равна вероятность того, что извлеченный из урны шар имеет красный цвет? Так как из четырех шаров два имеют красный цвет, то Р (А) == 2/4 =1/2. Рассуждая аналогично, найдем Р(В)==1/2, Р (С) = 1/2.. Придем к выводу, что события А, В и С попарно независимы. Независимы ли эти события в совокупности? Оказывается, нет. Допустив, что события В и С произошли, приходим к выводу, что событие А обязательно наступит. Следовательно, это событие достоверное и вероятность его равна единице.
Несколько событий называют попарно независимыми» если каждые два из них независимы. Например, события А, В, С попарно независимы, если независимы события А и В, А и С, В и С. Для того чтобы обобщить теорему умножения на несколько событий, введем понятие независимости событий в совокупности. Несколько событий называют независимыми в совокупности (или просто независимыми), если независимы каждые два из них и независимы каждое событие и все возможные произведения остальных. Условная вероятность появления любого события из них равна, его безусловной вероятности. если несколько событий независимы попарно, то отсюда еще не следует их независимость в совокупности требование независимости событий в совокупности сильнее требования их попарной независимости. Поясним сказанное на примере. Пусть в урне имеется 4 шара, окрашенные: один—в красный цвет (А), один— в синий цвет (В), один—в черный цвет (С) и один—во все эти три цвета (АВС). Чему равна вероятность того, что извлеченный из урны шар имеет красный цвет? Так как из четырех шаров два имеют красный цвет, то Р (А) == 2/4 =1/2. Рассуждая аналогично, найдем Р(В)==1/2, Р (С) = 1/2.. Придем к выводу, что события А, В и С попарно независимы. Независимы ли эти события в совокупности? Оказывается, нет. Допустив, что события В и С произошли, приходим к выводу, что событие А обязательно наступит. Следовательно, это событие достоверное и вероятность его равна единице.
 Следствие. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:
Следствие. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий: 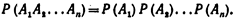 Доказательство. Рассмотрим три события: А, В и С. Совмещение событий А, В и С равносильно совмещению событий АВ и С. Поэтому
Доказательство. Рассмотрим три события: А, В и С. Совмещение событий А, В и С равносильно совмещению событий АВ и С. Поэтому 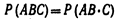 Так как события А, В и С независимы в совокупности, то независимы, в частности, события АВ и С, а также А и В. По теореме умножения для двух независимых событий имеем:
Так как события А, В и С независимы в совокупности, то независимы, в частности, события АВ и С, а также А и В. По теореме умножения для двух независимых событий имеем: 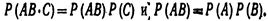 Итак. окончательно получим
Итак. окончательно получим  Для произвольного «п» доказательство проводится методом математической индукции.
Для произвольного «п» доказательство проводится методом математической индукции. 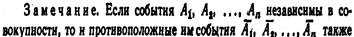 независимы в совокупности.
независимы в совокупности.
15. Теорема о вероятности появления хотя бы одного независимого события из совокупности, её условия и доказательство, частный случай данной теоремы для событий, имеющих одинаковую вероятность. Пример применения данной теоремы.
Пусть в результате испытания могут появиться п событий, независимых в совокупности, либо некоторые из них (в частности, только одно или ни одного), причем вероятности появления каждого из событий известны. Как найти вероятность того, что наступит хотя бы одно из этих событий? Теорема. Вероятность появления хотя бы одного из соб. А1….Аn независимых в совокупности, равна разности между единицей и произв.вероятн. противоп.соб. Р(А) = 1 – q1q2…qn Доказательство. Обозначим через А событие. Состоящее в появлении хотя бы одного из соб.А1…Аn. сумма вероятностей Соб. А и им противоположных равна единице  Отсюда, пользуясь теоремой умножения, получим
Отсюда, пользуясь теоремой умножения, получим 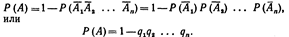

Пример 1. Вероятности попадания в цель при стрельбе из трех орудий таковы: p1=0, 8; P2=0, 7 Рз==0, 9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий. Решение. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий- поэтому рас-

16. Теорема сложения вероятностей для двух совместных событий: её условие применения, словесная формулировка, математическая запись, её доказательство. Замечания теоремы для зависимых, независимых и несовместных событий.
Два события называют совместными если появление одного из них не исключает появления другого в одном и том же испытании.Пример 1. А— появление четырех очков при бросании игральной кости; В— появление четного числа очков. События А и В— совместные.Пусть события А и В совместны, причем даны вероятности этих событий и вероятность их.совместного появления. Как найти вероятность события А+В, состоящего в том, что появится хотя бы одно из событий А и В? Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления: 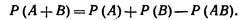 Доказательство. события А и В, по условию, совместны, А + В наступит, если наступит одно из следующих трех несовместных событий:
Доказательство. события А и В, по условию, совместны, А + В наступит, если наступит одно из следующих трех несовместных событий:

Событие А произойдет, если наступит одно из двух несовместных событий: А B¯ или А В. По теореме сложения вероятностей несовместных событий имеем 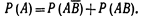 Отсюда
Отсюда 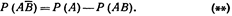 Аналогично имеем
Аналогично имеем 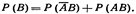 Отсюда
Отсюда 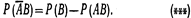 Подставив (**) и (***) в (*), окончательно получим
Подставив (**) и (***) в (*), окончательно получим 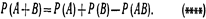 Замечание 1. При использовании полученной формулы следует иметь в виду, что события А и В могут быть как независимыми, так и зависимыми. Для независимых событий
Замечание 1. При использовании полученной формулы следует иметь в виду, что события А и В могут быть как независимыми, так и зависимыми. Для независимых событий 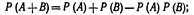 Для зависимых событий
Для зависимых событий 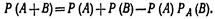
Замечание 2. Если события А и В несовместны, то их сов- 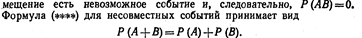
Мы вновь получили теорему сложения для несовместных событий.
Таким образом, формула (****) справедлива как для совместных, так и для несовместных событий. Пример 2. Вероятности попадания в цель при стрельбе первого 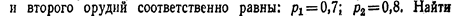 вероятность попадания при одном залпе (из обоих орудий) хотя бы одним из орудий.Решение. Вероятность попадания в цель каждым из орудий не зависит от результата стрельбы из другого орудия, поэтому события А (попадание первого орудия) и В (попадание второго орудия) независимы. Вероятность события АВ (оба орудия дали попадание)
вероятность попадания при одном залпе (из обоих орудий) хотя бы одним из орудий.Решение. Вероятность попадания в цель каждым из орудий не зависит от результата стрельбы из другого орудия, поэтому события А (попадание первого орудия) и В (попадание второго орудия) независимы. Вероятность события АВ (оба орудия дали попадание) 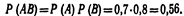
Искомая вероятность 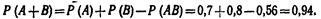 Замечание. Так как в настоящем примере события А и В независимые, то можно было воспользоваться формулой Р=1—
Замечание. Так как в настоящем примере события А и В независимые, то можно было воспользоваться формулой Р=1—
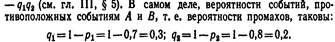
Искомая вероятность того, что при одном залпе хотя бы одно орудие даст попадание, равна  Как и следовало ожидать, получен тот же результат.
Как и следовало ожидать, получен тот же результат.
17. Теорема о формуле полной вероятности: её условие применения, словесная формулировка, математическая запись, её доказательство.
Пусть событие А может наступить при условии появления одного из несовместных событий В1, В2, ..., Вn (гипотез), которые образуют полную группу. Пусть известны вероятности этих событий (Р(Вi) и условные вероятности РВ1(А), РВ2(А), … РВn(А) события А. Как найти вероятность события А?.Теорема. Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий B1 B2,..., Вп образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:
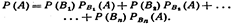 «формула полной вероятности». Доказательство. появление события А означает осуществление одного, безразлично какого, из несовместных событий В1А, В2А, В3А, ….., ВПА. Пользуясь теоремой сложения. Для несовместных событий получим
«формула полной вероятности». Доказательство. появление события А означает осуществление одного, безразлично какого, из несовместных событий В1А, В2А, В3А, ….., ВПА. Пользуясь теоремой сложения. Для несовместных событий получим 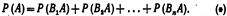 По теореме умножения вероятностей зависимых событий имеем
По теореме умножения вероятностей зависимых событий имеем 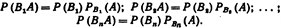
получим формулу полной вероятности 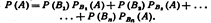
Пример 1. Имеется два набора деталей. Вероятность того, что деталь первого набора стандартна, равна 0, 8, а второго—0, 9. Найти вероятность того, что взятая наудачу деталь (из наудачу взятого набора)—стандартная.Решение. Обозначим через А событие «извлеченная деталь стандартна».Деталь может быть извлечена, либо из первого набора (событие В1), либо из второго (событие В2).Вероятность того. что деталь вынута из первого набора.Р(В1)=1/2. Вероятность того, что деталь вынута из второго набора.Р(В2)=1/2.
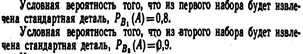 Искомая вероятность
Искомая вероятность 
18. Понятие гипотез. Постановка задачи и вывод формул Бейеса. Что позволяют формулы Бейса?
Пусть событие А может наступить при условии появления одного из несовместных событий В1, В2, В3, …. Вn, образующих полную группу. Поскольку заранее неизвестно, какое из этих событий наступит, их называют гипотезами.
Вероятность появления события А определяется по формуле полной вероятности
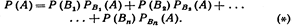 Допустим, что произведено испытание, в результате которого появилось событие А. Поставим своей задачей определить, как изменились вероятности гипотез. будем искать условные вероятности
Допустим, что произведено испытание, в результате которого появилось событие А. Поставим своей задачей определить, как изменились вероятности гипотез. будем искать условные вероятности 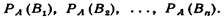

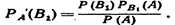 Отсюда Заменив здесь Р (А) по формуле (*)
Отсюда Заменив здесь Р (А) по формуле (*) 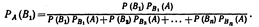
условная вероятность любой гипотезы Вi (i = 1, 2, …, n) может быть вычислена по формуле:
 Полученные формулы называют формулами Бейеса (по имени английского математика, который их вывел; опубликованы в 1764 г.). Формулы Бейеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А Пример. Детали, изготовляемые цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Вероятность того, что деталь попадает к первому контролеру, равна 0, 6, а ко второму—0, 4. Вероятность того, что годная деталь будет признана стандартной первым контролером, равна 0, 94, а вторым—0, 98. Годная деталь при проверке была признана стандартной. Найти вероятность того, что эту деталь проверил первый контролер. Решение. Обозначим через А событие, состоящее в том, что годная деталь признана стандартной. Можно сделать два предположения (гипотезы): 1) деталь проверил первый контролер (гипотеза В1); 2) деталь проверил второй контролер (гипотеза B2). Искомую вероятность того, что деталь проверил первый контролер, найдем по Формуле Бейеса:
Полученные формулы называют формулами Бейеса (по имени английского математика, который их вывел; опубликованы в 1764 г.). Формулы Бейеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А Пример. Детали, изготовляемые цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Вероятность того, что деталь попадает к первому контролеру, равна 0, 6, а ко второму—0, 4. Вероятность того, что годная деталь будет признана стандартной первым контролером, равна 0, 94, а вторым—0, 98. Годная деталь при проверке была признана стандартной. Найти вероятность того, что эту деталь проверил первый контролер. Решение. Обозначим через А событие, состоящее в том, что годная деталь признана стандартной. Можно сделать два предположения (гипотезы): 1) деталь проверил первый контролер (гипотеза В1); 2) деталь проверил второй контролер (гипотеза B2). Искомую вероятность того, что деталь проверил первый контролер, найдем по Формуле Бейеса:
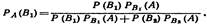 По условию задачи имеем:
По условию задачи имеем:
 Искомая вероятность
Искомая вероятность 
Как видно, до испытания вероятность гипотезы В1 равнялась 0, 6, а после того, как стал известен результат испытания, вероятность этой гипотезы (точнее, условная вероятность) изменилась и стала равной 0, 59. Таким образом, использование формулы Бейеса позволило переоценить вероятность рассматриваемой гипотезы.
19. Постановка задачи на ввод и вывод формулы Бернулли. Необходимые условия для применения формулы Бернулли.
Если производится несколько испытаний, причем вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А. В разных независимых испытаниях событие А может иметь либо различные, либо одну и ту же вероятность. Соб.А имеет одну и ту же вероятность. сложное событие - совмещение нескольких отдельных событий, которые называют простыми.
n независимых испытаний(событие А появиться либо не появиться). вероятность события А в каждом испытании одна и та же, а именно равна р. вероятность ненаступления события А в каждом испытании также постоянна и равна 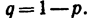 Поставим перед собой задачувычислить вероятность того, что при п испытаниях событие А осуществится ровно k раз и, следовательно, не осуществится п—k раз.
Поставим перед собой задачувычислить вероятность того, что при п испытаниях событие А осуществится ровно k раз и, следовательно, не осуществится п—k раз.
 испытаниях событие появится ровно 3 раза и, следовательно, не наступит 2 раза. Поставленную задачу можно решить с помощью так называемой формулы Бернулли.
испытаниях событие появится ровно 3 раза и, следовательно, не наступит 2 раза. Поставленную задачу можно решить с помощью так называемой формулы Бернулли.
Вывод формулы Бернулли. Вероятность одного сложного события, состоящего в том, что в п испытаниях событие А наступит k раз и не наступит п—k раз, по теореме умножения вероятностей независимых событий
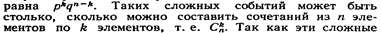
события несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме вероятностей всех возможных сложных событий. Поскольку же вероятности всех этих сложных событий одинаковы, то искомая вероятность равна вероятности одного сложного события, умноженной на их число: 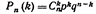
или 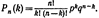 Полученную формулу называют формулой Бернулли. Пример. Вероятность того, что расход электроэнергии в продолжение одних суток не превысит установленной нормы, равна р-=0, 75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.Решение. Вероятность нормального расхода электроэнергии в продолжение каждых из 6 суток постоянна и равна р=0, 75. Следовательно.вероятность перерасхода электроэнергии в каждые сутки
Полученную формулу называют формулой Бернулли. Пример. Вероятность того, что расход электроэнергии в продолжение одних суток не превысит установленной нормы, равна р-=0, 75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.Решение. Вероятность нормального расхода электроэнергии в продолжение каждых из 6 суток постоянна и равна р=0, 75. Следовательно.вероятность перерасхода электроэнергии в каждые сутки 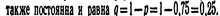
Искомая вероятность по формуле Бернулли равна 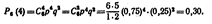 пользоваться формулой Бернулли при больших значениях «п» достаточно трудно, так как формула требует выполнения действий над громадными числами
пользоваться формулой Бернулли при больших значениях «п» достаточно трудно, так как формула требует выполнения действий над громадными числами
20. Локальная теорема Лапласа: условия её применения, математическая запись теоремы, математическая формула и основное свойство функции используемой в этой теореме.
Локальная теорема Лапласа дает асимптотическую формулу, которая позволяет приближенно найти вероятность появления события ровно k раз в п испытаниях, если число испытаний достаточно велико. Заметим, что для частного случая, а именно для р= 1/2, асимптотическая формула была найдена в 1730 г. Муавром; в 1783 г. Лаплас обобщил формулу Муавра для произвольного «р», отличного от 0 и 1. Поэтому теорему, о которой здесь идет речь, иногда называют теоремой Муавра—Лапласа. теорема. Если вероятность «р» появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность 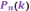 того, что событие А появится в «n» испытаниях ровно «k» раз приближенно равна (тем точнее, чем больше «n») значению функции
того, что событие А появится в «n» испытаниях ровно «k» раз приближенно равна (тем точнее, чем больше «n») значению функции 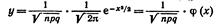
 ным значениям аргумента х (см. приложение 1). Для отрицательных значений аргумента пользуются теми же
ным значениям аргумента х (см. приложение 1). Для отрицательных значений аргумента пользуются теми же 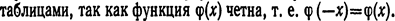
Итак, вероятность того, что событие А появится в п независимых испытаниях ровно k раз, приближенно равна
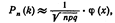
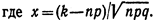 Пример 1. Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0, 2.
Пример 1. Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0, 2.
Решение. По условию, п==400; к==80; р==0, 2; q==0, 8. Воспользуемся асимптотической формулой Лапласа:
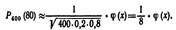 Вычислим определяемое данными задачи значение х:
Вычислим определяемое данными задачи значение х: 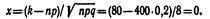
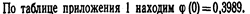 Искомая вероятность
Искомая вероятность 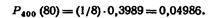
21. Интегральная теорема Лапласа: условия её применения, словесная формулировка, математическая запись теоремы, вывод формулы с использованием функции Лапласа, основные два свойства функции Лапласа.
производится «п» испытаний. в каждом из которых вероятность появления события А постоянна и равна р(0< р< 1).Как вычислить вероятность Рn(к1, к2)того, что соб.А появится в n испытаниях не менее к1 и не более к2 раз. Теорема.Если вероятность «р» наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то веротн. Рn(к1, к2) того, что соб.А появится в n испытаниях от к1 до к2 раз, приближ. Равна определенному интегралу. 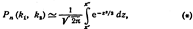
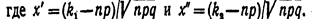
при решении задач, требующих применения интегральной теоремы Лапласа, пользуются специальнымитабли-
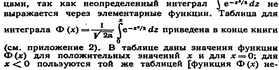
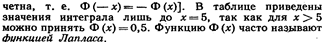
Для того чтобы можно было пользоваться таблицей функции Лапласа, преобразуем соотношение (*) так:
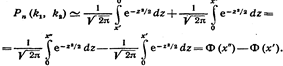 Итак, вероятность того, что событие А появится в п независимых испытаниях от k1. до k2 раз,
Итак, вероятность того, что событие А появится в п независимых испытаниях от k1. до k2 раз, 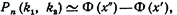
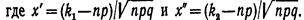
Приведем примеры, иллюстрирующие применение интегральной теоремы Лапласа. Пример. Вероятность того, что деталь не прошла проверку ОТК, равна р=0, 2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей. Решение. По условию, р==0, 2; q=0, 8; n==400; k1=70; K2=100. Замечание. Обозначим через т число появлений события А при п независимых испытаниях, в каждом из которых вероятность наступления события А постоянна и равна р. Если число т изме- 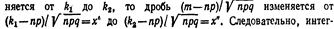
ральную теорему Лапласа можно записать и так:  Эта форма записи будет использоваться далее.
Эта форма записи будет использоваться далее.
22. Понятие случайной величины (СВ), правила обозначения СВ и возможных значений СВ. Понятие дискретной и непрерывной СВ, их примеры.
Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.Пример 1. Число родившихся мальчиков среди ста новорожденных есть случайная величина, которая имеет следующие возможные значения: 0, 1, 2,..., 100.Будем далее обозначать случайные величины прописными буквами X, Y, Z, а их возможные значения—соответствующими строчными буквами х, у, г можно заключить о целесообразности различать случайные величины, принимающие лишь отдельные, изолированные значения, и случайные величины, возможные значения которых сплошь заполняют некоторый промежуток. Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным. Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений непрерывной случайной величины бесконечно.Замечание. Настоящее определение непрерывной случайной величины не является точным. Более строгое определение будет дано позднее.
23. Понятие закона распределения дискретной случайной величины (ДСВ), способы задания закона ДСВ и их особенности, примеры способов задания законов ДСВ.
случайные величины могут иметь одинаковые перечни возможных значений, а их вероятности— различные. Поэтому для задания дискретной случайной величины недостаточно перечислить все возможные ее значения, нужно еще указать их вероятности. Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями. Его можно задать таблично, аналитически (в виде формулы) и графически. При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая—их вероятности: 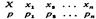 сумма вероятностей второй строки таблицы, равна единице
сумма вероятностей второй строки таблицы, равна единице  Если множество возможных значений Х бесконечно (счетно), то ряд р1 +р2+••• сходится и его сумма равна единице.имПример. В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 руб. и десять выигрышей по 1 руб. Найти закон распределения случайной величины Х—стоимости возможного выигрыша для владельца одного лотерейного билета. Решение. Напишем возможные значения X: X1= 50, х2= 1, X3==0. Вероятности этих возможных значений таковы: p1==0, 01, р2 == 0, 1, Рз = 1 - (P1 + Р2) = 0.89.Напишем искомый закон распределения: Х 50 10 О р 0, 01 0, 1 0, 89 Контроль: 0, 01+0, 1+0, 89=1.Графически: в прямоугольной системе координат строят точки (Xi,. Pi), а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником, распределения.
Если множество возможных значений Х бесконечно (счетно), то ряд р1 +р2+••• сходится и его сумма равна единице.имПример. В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 руб. и десять выигрышей по 1 руб. Найти закон распределения случайной величины Х—стоимости возможного выигрыша для владельца одного лотерейного билета. Решение. Напишем возможные значения X: X1= 50, х2= 1, X3==0. Вероятности этих возможных значений таковы: p1==0, 01, р2 == 0, 1, Рз = 1 - (P1 + Р2) = 0.89.Напишем искомый закон распределения: Х 50 10 О р 0, 01 0, 1 0, 89 Контроль: 0, 01+0, 1+0, 89=1.Графически: в прямоугольной системе координат строят точки (Xi,. Pi), а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником, распределения.
24. Биномиальный закон распределения дискретной случайной величины (ДСВ): постановка задачи, условия применения, вывод аналитического выражения, табличный способ задания, причина данного названия распределения.
Пусть производится п независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Вероятность наступления события во всех испытаниях постоянна и равна р (следовательно, вероятность непоявления q =1— р). в качестве дискретной случайной величины Х - число появлений события А в этих испытаниях. найти закон распределения величины X.
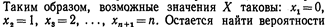
этих возможных значений, для чего достаточно воспользоваться формулой Бернулли: 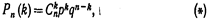
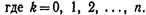 Формула (*) и является аналитическим выражением искомого закона распределения. Биномиальным называют распределение вероятностей, определяемое формулой Бернулли. Закон назван «биномиальным» потому, что правую часть равенства (*) можно рассматривать как общий член разложения бинома Ньютона:
Формула (*) и является аналитическим выражением искомого закона распределения. Биномиальным называют распределение вероятностей, определяемое формулой Бернулли. Закон назван «биномиальным» потому, что правую часть равенства (*) можно рассматривать как общий член разложения бинома Ньютона: 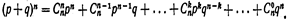 Т.о, первый член разложения рn определяет вероятность наступления рассматриваемого события
Т.о, первый член разложения рn определяет вероятность наступления рассматриваемого события
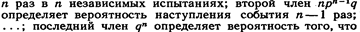 событие не появится ни разу.Напишем биномиальный закон в виде таблицы:
событие не появится ни разу.Напишем биномиальный закон в виде таблицы: 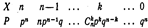 Пример. Монета брошена 2 раза. Написать в виде таблицы закон распределения случайной величины Х—числа выпадений «герба».
Пример. Монета брошена 2 раза. Написать в виде таблицы закон распределения случайной величины Х—числа выпадений «герба».
Решение. Вероятность появления < герба» в каждом бросании 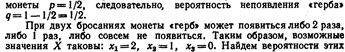 возможных значений по формуле Бернулли:
возможных значений по формуле Бернулли:
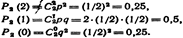 Напишем искомый закон распределения:
Напишем искомый закон распределения: 
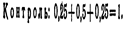
25. Распределение Пуассона для дискретной случайной величины (ДСВ): постановка задачи, условия применения, вывод аналитического выражения.
Пусть производится п независимых испытаний, в каждом из которых вероятность появления события А равна р. Для определения вероятности k появлений события в этих испытаниях используют формулу Бернулли. Если же п велико, то пользуются асимптотической формулой Лапласа. Однако эта формула непригодна, если вероятность события мала (Р≤ 0, 1). В этих случаях (п велико, р мало) прибегают к асимптотической формуле Пуассона.найти вероятность того, что при очень большом числе испытаний, в каждом из которых вероятность события очень мала, событие наступит ровно k раз. Сделаем важное допущение: произведение пр сохраняет постоянное значение, а именно пр=λ. неизменным.
Воспользуемся формулой Бернулли для вычисления, интересующей нас вероятности: 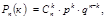 но т.к. из формул комбинаторики известно, что число размещений
но т.к. из формул комбинаторики известно, что число размещений 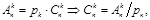 при этом
при этом 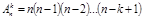 . Тогда можно записать:
. Тогда можно записать: 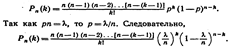
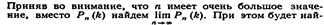
дено лишь приближенное значение отыскиваемой вероятности, что поскольку произведение пр сохраняет постоянное значение, то при 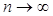 , вероятность
, вероятность 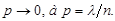 Причём
Причём 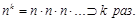
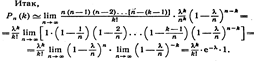
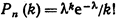 Эта формула выражает закон распределения Пуассона вероятностей массовых (п велико) и редких (р мало) событий. Замечание. Имеются специальные таблицы, пользуясь которыми можно найти Pn(к), зная k и λ. Пример. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равно 0, 0002. Найти вероятность того. что на базу прибудут 3 негодных изделия.
Эта формула выражает закон распределения Пуассона вероятностей массовых (п велико) и редких (р мало) событий. Замечание. Имеются специальные таблицы, пользуясь которыми можно найти Pn(к), зная k и λ. Пример. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равно 0, 0002. Найти вероятность того. что на базу прибудут 3 негодных изделия.
26. Геометрическое распределение дискретной случайной величины (ДСВ): постановка задачи, условия применения, вывод аналитического выражения, причина данного названия распределения.
Пусть производятся независимые испытания, в каждом из которых вероятность появления события Аравна р(0< р< 1)ианалогично вероятн.непоявления. если событие А появилось в к-м испытании, то в предшествующих k—1 испытаниях оно не появлялось.Обозначим через Х дискретную случайную величину — число испытаний, которые нужно провести до первого появления события А. Очевидно, возможными значениями Х являются натур.числа х1=1…Пусть в первых к-1 испыт.соб.А не наступило, а в к-ом появилось. Вероятн. этого «сложного события», по теореме умножения вероятностей независимых событий,  Получим прогресию: р, qp, q2p(квадрат), …qk-1p…(**) распределение (*) называют геометрическим. Легко убедиться, что ряд (**) сходится и сумма его равна единице. Действительно, сумма ряда (**)
Получим прогресию: р, qp, q2p(квадрат), …qk-1p…(**) распределение (*) называют геометрическим. Легко убедиться, что ряд (**) сходится и сумма его равна единице. Действительно, сумма ряда (**) 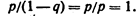 Пример. Из орудия производится стрельба по цели до первого попадания. Вероятность попадания в цель р== 0, 6. Найти вероятность того, что попадание произойдет при третьем выстреле.Решение. По условию, р==0.6, q=0, 4. k=3. Искомая вероятность по формуле (*.)
Пример. Из орудия производится стрельба по цели до первого попадания. Вероятность попадания в цель р== 0, 6. Найти вероятность того, что попадание произойдет при третьем выстреле.Решение. По условию, р==0.6, q=0, 4. k=3. Искомая вероятность по формуле (*.) 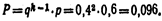
27. Понятие и необходимость использования числовых характеристик случайной величины. Понятие математического ожидания (МОЖ) дискретной случайной величины (ДСВ), развёрнутая и свёрнутая запись формулы по вычислению МОЖ ДСВ. Замечание к определению МОЖ.
закон распределения полностью характеризует случайную величину. Однако часто закон распределения неизвестен Иногда выгоднее пользоваться числами (обобщёнными) - такие числа называют числовыми характеристиками случайной величины. К числу важных относится мож. Мож, приближенно равно среднему значению случайной величины. Математическое ожидание дискретной случайной величины. Математическим ожиданием дискретной случайной величины называют сумму произведений всех её возможных значений на их вероятности.
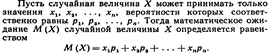 Если дискретная случайная величина Х принимает счетное множество возможных значений, то
Если дискретная случайная величина Х принимает счетное множество возможных значений, то