Высказывания. Логические операции с высказываниями. Тождественно-истинные формулы. Правильные рассуждения. Проблема разрешимости в алгебре высказываний.

Математическая логика – это современный вид форматной логики, т.е. науки изучающей умозаключения, с точки зрения их формального строения.

Высказывания:

Под высказыванием будем понимать такое утверждение, относительно которого имеет смысл говорить, истинно оно или ложно. Л - 0 - ложь; И - 1 - истина {0, 1} - множество истинностных значений.

Логические операции с высказываниями:

1) Отрицанием высказывания U (Ū, U) называется такое высказывание, которое истинно тогда и только тогда, когда U ложно, и ложно, когда U истинно.

2) Конъюнкция двух высказываний P и Q – это такое высказывание, которое истина тогда и только тогда, когда оба высказывания истинны, во всех остальных случаях оно ложно. Обозначения: P& Q, PQ, PΛ Q. В русском языке соответствует союзам: и, а, но.

3) Дизъюнкция двух высказываний P и Q – это такое высказывание, которое ложно тогда и только тогда, когда оба высказывания ложны, во всех остальных случаях оно истинно. Обозначение: P V Q. В русском языке соответствует союзу или.

4) Импликацией высказываний P и Q называется такое

высказывание, которое ложно тогда и только тогда, когда P истинно, а Q ложно, во всех остальных случаях оно истинно. Обозначение: P → Q. (Если P, то Q).

5) Эквиваленцией двух высказываний P и Q называется высказывание, которое истинно тогда и только тогда, когда совпадают истинностные значения высказываний P и Q. Обозначения: 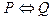, P~Q. (Необходимо и достаточно).

6) Сложение по модулю два a b = 1, если значения a и b различны, a b = 0 – значения a и b совпадают

P	Q	P	P& Q	P→ Q	P V Q	P~Q	P Q
0	0	1	0	1	0	1	0
0	1	1	0	1	1	0	1
1	0	0	0	0	1	0	1
1	1	0	1	1	1	1	0

Тождественно-истинные формулы:

Пусть формула А зависит от списка переменных < x₁, x₂,..., x_n>.

Формула А называется выполнимой, если на некоторой оценке списка переменных она принимает значения равные 1.

Формула А называется тождественно-истинной или тавтологией, если на любой оценке списка переменных она принимает значения равные 1.

Формула А называется опровержимой, если на некоторой оценке списка переменных она принимает значения равные 0.

Формула А называется тождественно-ложной, если на всех оценках списка переменных она принимает значения равные 0.

Тождественно-истинные формулы играют роль логических законов. При подстановке в эти формулы высказываний вместо переменных будем получать истинные высказывания.

Основные тавтологии:

Пусть А, В и С – произвольные формулы.

A V Ā (закон исключенного третьего); A → A; A → (B → A);

(A → B) → ((B → C) → (A → C));

A& B → A A& B → B A → (A V B) B → (A V B)

Все эти тавтологии могут быть доказаны с помощью таблиц истинности.

Правильные рассуждения:

Под рассуждением будем понимать процесс получения новых знаний, выраженных высказываниями из ранее полученных знаний также представленных высказываниями. Схема любого доказательства или рассуждения записывается следующим образом:

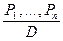, где Р_i – посылка (исходные высказывания), D – заключение (полученные высказывания).

Рассуждение называется правильным, если из конъюнкции посылок следует заключение, т.е. всякий раз, когда посылки являются истинными, заключение тоже является истинным. Для проверки правильности рассуждений нужно показать, что формула: является истинной.

Основные схемы правильных рассуждений:

Правило заключения (Modus Ponens)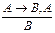

Правило отрицания (Modus Tollens)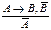

Пр-ло утверждения отрицания

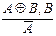
Правило отрицания утверждения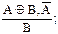

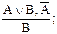
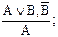
Правило транзитивности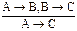

Закон противоречий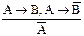

Закон контрпозиции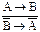

Проблема разрешимости в алгебре высказываний:

Проблема разрешимости: существует ли алгоритм, который позволил бы за конечное число шагов определить, является ли указанная формула тождественно-истинной или нет. В логике высказываний проблема разрешимости имеет решение.

Теорема: Формула А является тавтологией тогда и только тогда, когда в ее КНФ каждый конъюнктивный член содержит некоторую переменную и ее отрицание.

Теорема: Формула А является тождественно-ложной тогда и только тогда, когда в ее ДНФ каждый дизъюнктивный член содержит некоторую переменную и ее отрицание.

Предикаты. Понятие предиката. Логические операции с предикатами. Операции с кванторами. Свободные и связанные переменные. Формулы логики предикатов. Интерпретация формул. Равносильность формул. Приведенная и нормальная формы формул.

Предикаты. Понятие предиката:

Логика предикатов разбивает любое высказывание на субъект и предикат.

Субъект - это то, о чем говорится в данном утвержднии.

Предикат - это то, что утверждается о субъекте.

Пример: «4 - четное число». «4» - субъект, «четное число» - предикат.

Одноместным предикатом Р(х) называется функция переменного х, определенная на некотором множестве М и принимающая значения из множества { 0, 1}.

Множество М называется областью определения предикатов. Множество значений х из множества М, для которых Р(х) = 1, называется областью истинности данного предиката:

I_p = { x 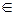M | P(x) = 1}

Р(х): х - четное число; М = N, I_P = { 2, 4, 6,...}.

Одноместные предикаты выражают свойства предметов. Предикат Р(х) называется тождественно истинным, если I_P = М (область истинности совпадает с множеством М), и тождественно ложным, если .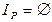

n-местным предикатом Р(х₁,..., х_n) называется функция, определенная на множестве и принимающая значения из множества { 0, 1}.

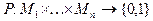
Пример: Р(x, y): x < y P(2, 3) - истина, т.к. 2< 3 P(3, 2) - ложь.

Предикат можно рассматривать как переменное высказывание, которое при некоторых значениях элемента является истинным, при других - ложным.

Логические операции с предикатами:

Конъюнкция: P(x)& Q(x) I_{P& Q}=I_P∩ I_Q;

Дизъюнкция: P(x) V Q(x) I_PVQ=I_P 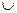I_Q;

Отрицание: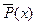

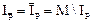
Импликация: 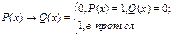[A → B ≡ Ā V B] ;

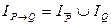Эквиваленция: P(x) ~ Q(x) 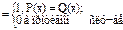[A~E≡ (A& E)V(Ā & Ē)] I_A~E = (I_A ∩ I_E) 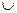(I _Ā ∩ I_Ē )

Операции с кванторами. Свободные и связанные переменные:

1)Квантор общности:

Пусть Р(х) - предикат, определенный на множестве М. Под высказыванием 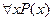(для любого х выполняется Р(х)) будем понимать высказывание, которое истинно тогда и только тогда, когда Р(х) = 1 для любого 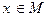, и ложно в противном случае.

2)Квантор существования:

Под выражением (существует х, для которого выполняется Р(х)) будем понимать высказывание, которое истинно тогда и только тогда, когда существует хотя бы один 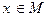, для которого Р(х) = 1, и ложно в противном случае.

Переход от предиката Р(х) к выражению 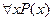или называется связыванием переменной х или операцией навешивания квантора на переменную х. Та переменная, на которую навешен квантор, называется связанной. Несвязанная переменная называется свободной.

Р(х): х - четное число, М = N

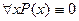
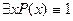
Если переменная в формуле является связанной, то данная формула не зависит от этой переменой, а это означает, что связанную переменную можно переименовывать, от этого значение формулы не изменится.

Навешивание квантора на одноместный предикат превращает его в высказывание, т.е. нульместный предикат. Кванторы можно навешивать на свободные переменные n-местных предикатов, что понижает порядок предиката на единицу.

P(x₁,..., x_n) - n-местный предикат 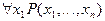– (n - 1)-местный предикат

Кванторы можно навешивать на переменную в формуле: . Для этого выражение, на которое навешивается квантор, заключается в скобки. Выражение, на которое навешен квантор, называется областью действия квантора.

Формулы логики предикатов:

Алфавит логики предикатов состоит из следующих символов:

1) символы предметных переменных: х₁,..., х_n;

2) предикатные символы: P, Q, R,...;

3) логические связки: ;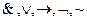

4) символы квантора: ;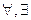

5) круглые скобки () и запятая.

Слово в логике предикатов называется формулой, если оно удовлетворяет следующим условиям: 1.Слово P(x₁,..., x_n) является формулой. Эта формула называется атомарной (или простейшей); 2. Если А - формула логики предикатов, то Ā - тоже формула логики предикатов, причем все связанные и свободные переменные формулы А совпадают соответственно со связанными и свободными переменными формулы Ā;

3.Пусть А и В – формулы, причем нет такой переменной, которая была бы свободной в одной формуле и связанной в другой, тогда (A& B), (AVB), (A~B), (A→ B) – тоже формулы;

1)Пусть А - формула, в которой х является свободной переменной, тогда 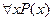или также является формулой, в которой переменная х является связанной. Все остальные переменные полученных формул и формулы А совпадают;

2)Слово является формулой тогда и только тогда, когда оно удовлетворяет свойствам 1-4.

Примеры:

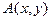– атамарная формула, где x, y - свободные переменные;

– формула, где x - связанная, y - свободная переменная;

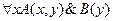– формула;

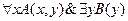– не является формулой, т.к. в одной формуле переменная y - свободная, а в другой – связанная. Ни одна переменная в формуле не может быть одновременно свободной и связанной.

Интерпретация формул:

Под интерпретацией формулы понимается система < M, f >, состоящая из не пустого множества М и соответствия f, которое каждому n-местному предикатному символу ставит в соответствие n- местный предикат.

При этом предполагается, что переменные предиката пробегают множество М.

Для заданной интерпретации любая формула, не содержащая свободных переменных, представляет собой высказывание, которое истинно или ложно.

Формула, содержащая свободные переменные, представляет собой предикат, который при одних значениях из М принимает истинное значение, а при других – ложное.

Если формула зависит от свободных переменных< х₁, х₂…x_n>, то для нахождения ее значения на наборе < а₁, а₂…а_n>, где а_i из М, достаточно подставить значение переменных в формулу и пользуясь интерпретацией, а так же значением логических связок определить искомое значение формулы.

Равносильность формул:

Пусть даны формулы А и В, имеющие одни и те же свободные переменные.

Формулы А и В равносильны в данной интерпретации, если на любом наборе свободных переменных они принимают одинаковые значения.

Формулы А и В называются равносильными на множестве М, если они равносильны в любой интерпретации, заданной на этом множестве.

Формулы А и В равносильны в логике предикатов, если они равносильны на любом множестве М.

ОСНОВНЫЕ РАВНОСИЛЬНОСТИ ЛОГИКИ ПРЕДИКАТОВ:

1)Основные равносильности логики высказываний;

2) Перенос квантора через отрицание: пусть формула А содержит свободную переменную х,

тогда справедливы следующие равносильности:

;

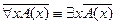
3) Вынос квантора за скобки:

а) пусть формула А содержит свободную переменную х, а формула В не зависит от х, тогда:

,

,

,

;

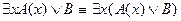б) если формула В содержит свободную переменную х, то в этом случае:

,

.

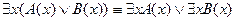Если в этих формулах заменить кванторы, то получатся формулы справедливые только в одну сторону:

,

;

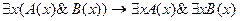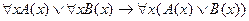4)Перестановка одноименных кванторов:

,

;

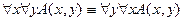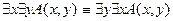5) Переименование связанной переменной: если в формуле А связанные переменные переименовать, то получится формула, равносильная данной:

.

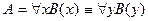Приведенная и нормальная формы формул:

Под длиной формулы будем понимать общее количество входящих в нее предикатных символов, логических связок и символов квантора.

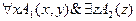, l = 5.

Формула, в которой из логических связок содержатся только операции 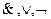, причем отрицание стоит над предикатными символами, называется приведенной формулой.

Примеры:

А(х, y) - атамарная формула всегда приведенная

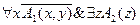- приведенная

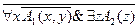- не приведенная.

Теорема: Для любой формулы логики предикатов можно указать равносильную ей приведенную формулу, причем множество свободных и связанных переменных указанных формул совпадают.

Полученная формула называется приведенной формой данной формулы.

Формула, которая является приведенной и не содержит кванторов, или все кванторы в этой формуле вынесены в начало формулы, называется нормальной формулой.

Теорема: Для любой приведенной формулы существует равносильная ей нормальная формула той же самой длины.

Полученная формула называется нормальной формой данной приведенной формулы.

Вывод: для любой формулы логики предикатов можно построить равносильную ей формулу, находящуюся в нормальной форме.

Вычислимые функции. Простейшие функции. Операции над функциями: суперпозиция функций, схема примитивной рекурсии, оператор минимизации. Примитивно-рекурсивные функции. Частично-рекурсивные и общерекурсивные функции.

Вычислимые функции:

Функция f (x₁ … x_n) называется эффективно вычислимой, если существует алгоритм, которая позволяет найти значение этой функции, если заданы значения ее аргументов (данное определение является интуитивным).

Класс (множество) вычислимых функций строится след образом:

1) вводятся простейшие функции, т.е. базис;

2) на множестве вычислимых ф-й вводятся операции с функциями, с помощью которых из простейших функций и ранее полученных строятся новые вычислимые функции.

Простейшие функции:

1)функция (оператор) сдвига l (x)= x +1

2)нуль-функция (оператор аннулирования) 0 (x)=0

3)проецирующая функция (оператор тождества) 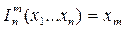, m – какая переменная выбирается, n – количество переменных; используется для введения фиктивных переменных

Простейшие функции определены для любого натурального аргумента и являются интуитивно вычислимыми.

Операции над функциями:

Суперпозиция функций

Рассмотрим функции f₁(x₁, …x_n), …, f_m(x₁, …x_n) и j (x₁, …x_m).

Функция Y(x₁, …x_n) называется суперпозицией функций f₁… f_m и j, если она получается по следующему правилу: Y(x₁, …x_n)= j (f₁(x₁, …x_n), …, f_m(x₁, …x_n)).

Если ф-я j (f₁, …, f_m) является эффективно вычислимой, то для вычисления функции j можно предложить следующий алгоритм:

1) фиксируем значения переменных x_i: положим x_i=a_i (i=1..n)

2) вычислим значения ф-й f₁, …, f_m на выбранном наборе значений переменных. f_i(a₁, …, a_n)=b_i (i=1..m)

3) вычислим значения j (b₁, …b_m)= Y(a₁, …a_n)=c

Если функции f₁… f_m, j определены для любого набора a₁…a_n, то и функция Y также определена для любого набора a₁…a_n. Если же хотя бы одна из функций f₁… f_m, j будет не определена на наборе a₁…a_n, то и функция Y будет не определена на данном наборе.

Обозначение: Y(x₁, …x_n)= 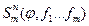m – сколько функций n – сколько аргументов у f

Если оп суперпозиции применить к простейшим функциям, которые являются всюду определенными, то получим всюду определенные функции.

Схема примитивной рекурсии:

Рассмотрим следующие функции: j (x₁, …, x_n) – n-местная функция, f(x₁, …, x_n, y) – (n+1)-местная функция, y(x₁, …, x_n, y, z) – (n+2)-местная функция.

Будем говорить, что функция f(x₁, …, x_n, y) получена из j и y по схеме примитивной рекурсии, если она удовлетворяет следующим условиям:

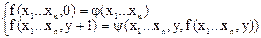
Рекурсия идет по одной переменной!

f(x₁, …, x_n, y)=R_n(j, y) (n – количество фиксированных переменных, т.е. тех, по которым переменная не идет).

Если функции j, y являются эффективно вычислимыми, то для вычисления функции f можно использовать следующий алгоритм:

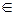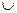1) положим x_i=a_i, i = 1 ÷ n, a_i N {0}

2) вычислим f(a₁, …, a_n, 0)= j (a₁, …, a_n) = b

3) вычислим f(a₁, …, a_n, 1)= y(a₁, …, a_n, 0, b)=C₁, и т.д. пока y не станет равным требуемому значению k

Если функции j, y являются всюду определенными, то и функция f, которая из них получается, будет всюду определенной.

Оператор минимизации:

Пусть дана функция f(x, y). Зафиксируем значение переменной x и найдем наименьшее значение y, при котором f(x, y)=0. Очевидно, что это значение y будет зависеть от x, т.е. получаем некоторую функцию, зависящую от x. j(x)=m y[f(x, y)=0] (минимальный у, для которого f(x, y)=0) m -оператор.

Аналогично для оп.минимизации для функций нескольких переменных:

j(x₁, … x_n)=m y[f(x₁, … x_n, y)=0]

Если функция fявляется эффективно вычислимой, то для вычисления функции j можно использовать следующий алгоритм:

1) зафиксируем x_i=a_i

2) вычислим f(a₁, …, a_n, 0). Если значение этой функции равно 0, то

j (a₁, …a_n)= 0. В противном случае - шаг 3)

3) вычислим f(a₁, …, a_n, 1). Если значение – 0, то j (a₁, …a_n)= 1, иначе – дальше, пока не получим f(a₁, …, a_n, k)= 0, j (a₁, …a_n)= k.

Если в результате работы данного алгоритма значение y не будет получено, то это означает, что функция j на данном наборе значений переменных не определена.

Пример. Дана функция f(x, y)=x-y

j(x, y)= m z[x-y-z=0] или j(x, y)= m z[x=y+z]

f(3, 1)

z=0 (3¹ 1+0)

z=1 (3¹ 1+1)

z=2(3=1+2)=> f(3, 1)=2

Примитивно-рекурсивные функции. Частично-рекурсивные и общерекурсивные функции:.

Функция называется примитивно-рекурсивной, если она может быть получена с помощью конечного числа операций суперпозиции и схемы примитивной рекурсии из множества простейших функций.

Функция f(x₁, …, x_n) называется частично-рекурсивной, если она может быть получена из простейших функций с помощью конечного числа операций суперпозиции, схемы примитивной рекурсии и m - оператора.

Функция f(x₁, …, x_n) называется общерекурсивной, если она является частично-рекурсивной и определена для любых значений аргументов из множества N и {0}, т.е. является всюду определенной.

Индуктивное определение примитивно-рекурсивной функции:

1) простейшие функции l(x), 0 (x), 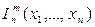являются примитивно-рекурсивными функциями

2) если функции j (x₁, …, x_m), f₁(x₁, …, x_n), …, f_m(x₁, …x_n) являются примитивно-рекурсивными функциями, то функция y(x₁, …, x_n), которая является их суперпозицией y(x₁, …, x_n) = 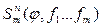также является примитивно-рекурсивной

3) если j (x₁, …, x_n), y(x₁, …, x_n, y, z) являются примитивно-рекурсивными, то и функция f(x₁, …, x_n, y) получена по схеме примитивной рекурсии f(x₁, …, x_n, y)=R_n(j, y) также являетсяпримитивно-рекурсивной

4) других примитивно-рекурсивных функций нет

Отсюда следует, что для доказательства примитивной рекурсивности функции достаточно показать, что она является либо простейшей функцией, либо получена из примитивно-рекурсивных функций с помощью операций суперпозиции, либо схемы примитивной рекурсии.

Примитивно-рекурсивные функции являются всюду определенными.

Пример. Показать, что f(x, y) является примитивно-рекурсивной функцией

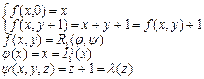
f(x, y) получена по схеме из простейших функций => она примитивно-рекурсивная.

Пример. f(x, y)=x+y+1 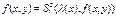- данная функция является примитивно-рекурсивной, т.к. она получена с помощью операции суперпозиции из простейшей функции l(x) и примитивно-рекурсивной функции f.

Тезис Черча: каждая эффективно-вычислимая функция является частично-рекурсивной

Основная теорема теории алгоритмов: функция f(x₁, …, x_n) вычислима по Тьюрингу тогда и только тогда, когда она является частично-рекурсивной функцией