
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Функционирование машины Тьюринга. Конструирование машин Тьюринга. Композиция машин. Вычислимые по Тьюрингу функции.
|
|
Функционирование машины Тьюринга:
Из трех основных понятий алгоритма, второе определение связано с машинной математикой. Алгоритм рассматривается как простейшее детерминированное устройство, способное в каждый момент времени выполнить простейшие операции. Основная модель – машина Тьюринга.
Машина Тьюринга работает с тремя алфавитами:
1. входной алфавит А ={ а0 … аn }, с помощью которого записывается входная, промежуточная, выходная информация. а0 – пустой символ (незначащий ноль, Ù, В, #), а1 – 1 или |
2. внутренний алфавит, или алфавит состояний Q ={ q0 … qm }, q0 - заключительное состояние q1 – начальное состояние q0…qn – рабочее состояние
3. алфавит сдвига {Л, В, Н} или {-1, +1, 0} (влево, вправо, на месте)
Машина Тьюринга состоит из следующих частей:
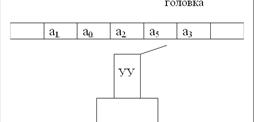
1) лента, потенциально бесконечная в обе стороны. Потенциальная бесконечность означает, что в каждый момент времени на ленте записано конечное слово, но в случае необходимости слева и справа от слова можно достроить необходимое количество ячеек. Лента разделена на ячейки, в каждой из которых записан только один символ входного алфавита. В пустых ячейках записан пустой символ. Если в ячейке информацию необходимо стереть, то достаточно записать в неё пустой символ.
2) управляющее устройство (УУ), которое с помощью программы управляет машиной Тьюринга. УУ в каждый момент времени может находиться только в одном из состояний алфавита Q.
3) головка (считывающее и записывающее устройство) в каждый момент времени выполняет следующие действия
· считывает символ, записанный в ячейке
· заменяет его на другой символ алфавита А или оставляет прежним
· сдвигается по ленте вправо, влево на одну ячейку или остается на месте
Правило работы машины Тьюринга:
Машина Тьюринга, находясь в состоянии qi и считывая символ aj, записывает в данную ячейку символ аk, переходит в состояние qe, осуществляет сдвиг. При этом говорят, что машина выполнила одну команду: ajqi ® akqeS SÎ {Л, П, Н}
Совокупность команд называется программой МТ.
ajqi – исходные символы команд должны быть различны. Если это условие выполняется, машина называется детерминированной, в противном случае – недетерминированной. Машина работает в дискретные моменты времени.
Таким образом, полное описание машины Тьюринга в каждый момент времени, по которому можно определить её дальнейшее поведение, содержит инфу о:
внутреннем состоянии, в котором находится машина, слове, которое записано на ленте, и о том символе, который считывается в данный момент времени. Полное состояние машины Тьюринга будем называть конфигурацией.
Работа машины Тьюринга может быть представлена как последовательность конфигураций k1 ® k2 ®…® kn.
Стандартная начальная конфигурация – считывание крайнего левого непустого символа в состояние q1
Стандартная заключительная конфигурация – машина перешла в заключительное состояние:
a
q0
Если машина перешла в заключительное состояние, она применима к данному входному слову, если работает бесконечно, значит, машина не применима к данному слову.
МТ представляет собой совокупность, состоящую из входного алфавита, алфавита состояний и программы. M = < A, Q, П>. А – входной алфавит Q – внутренний алфавит П – программа
Программа машины может быть задана следующим образом:
1) списком команд: ajqi ® akqnS
2) с помощью таблицы
| a0 | a1 | a2 | |
| q0 | ak, qm, S | ||
| q1 |
3) с помощью графа предикатов (вершины – состояния, каждой команде соответствует дуга)
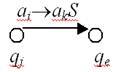
Конструирование машин Тьюринга:
Сконструировать машину Тьюринга – построить её программу. Проходит в два этапа:
1) словесное описание алгоритма решаемой задачи
2) перевод словесного описания алгоритма на язык машины Тьюринга (для этого задаются A, Q, П)
Пример: построить машину Тьюринга, которая вычисляет функцию f(n)=n+1, где n задано в двоичной системе исчисления.
А ={0, 1, a0 }, множество Q определяется в процессе построения программы.
Алгоритм:
1. перевести головку из крайнего правого состояния в крайнее левое
2. если в крайнем правом положении машина считывает 0, то положить в ячейку 1 и остановиться, если головка считывает 1, положить в ячейку 0 и сдвинуться на один шаг влево.
Повторить Шаг 2
Пример: На ленте записано натуральное десятичное число. Необходимо сконструировать машину Тьюринга, увеличивающую это число на 1. Изначально головка указывает на первую цифру числа. Получаем: A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a0}, Q = {q1, q2, q0}. П – см. таблицу.
| q1 | 0> q1 | 1> q1 | 2> q1 | 3> q1 | 4> q1 |
| q2 | 1=q0 | 2=q0 | 3=q0 | 4=q0 | 5=q0 |
| a0 | |||||
| 5> q1 | 6> q1 | 7> q1 | 8> q1 | 9> q1 | a0< q2 |
| 6=q0 | 7=q0 | 8=q0 | 9=q0 | 0< q2 | 1=q0 |
Общая идея – переместить головку на последнюю цифру числа, и если эта цифра не 9, то увеличить её на единицу, иначе обратить в ноль и перейти к предыдущей ячейке.
Композиция машин:
Композиция машин представляет собой последовательное выполнение двух машин.
Т1 =(A1, Q1, П1) Т2 =(A2, Q2, П2) Q1 Ç Q2 =Æ
Композицией машин Т1 ° Т2 называется машина Т (A, Q, П), где А = А1 È A2; Q =(Q1 È Q2)\{ q10 } (q10 – заключительное состояние Т1). Машина Т работает по следующему правилу: U – некоторое слово, Т (U)= Т1 ° Т2 (U)= Т2 (Т1 (U))
Теорема. Композиция машин Т1 ° Т2 существует.
Q1 ={ q10, q1, …, qn }
Q2 ={ q20, q`1 , …, q`n }, тогда для построения Q удалим состояние q10, переобозначив его в q n+1, которое совпадает с начальным состоянием второй машины, а все остальные состояния - в q` i= qn+ 1.
Вычислимые по Тьюрингу функции:
Функция f(x1…xn) называется вычислимой по Тьюрингу, если существует машина Тьюринга, вычисляющая значение этой функции, когда заданы значения аргументов. Функция f(x1…xn) задана на множестве натуральных чисел, но теория алгоритмов рассматривает расширенное множество натуральных чисел NÈ {0}.
Аргументы функции f(x1…xn) на ленте представляются в виде следующего слова:
Каждому аргументу соответствует столько палочек, каково значение этого аргумента. Если функция f определена на данном наборе значений переменной x1…xn, то в результате работы машины Тьюринга на ленте должно остаться такое количество палочек, записанных подряд, которое равно значению функции на данном наборе. Если функция f не определена на данном наборе, то машина Тьюринга должна работать бесконечно.
Начальная конфигурация – считывание крайней левой палочки.