II.III.I. Математическое описание событий

Статистическое определение вероятностей производится по данным опытов и всегда после них. В теории вероятностей исследуются способы исчисления вероятностей случайных событий на основе выявления связей между событиями без непосредственного проведения опыта.

Отдельные события, относящиеся к одному и тому же эксперименту, так или иначе, связаны друг с другом. Поэтому в теории вероятностей существенную роль играют средства описания событий.

Два события могут наступить одновременно или, наоборот, осуществление одного из них исключает появление другого. О таких событиях соответственно говорят, что они совместны или несовместны.

Для математического описания эксперимента G вводится понятие элементарных событий, называемых также исходами опыта. Множество возможных попарно несовместных событий W={w₁; w₂;...; w _n } таких, что всякое событие A может быть описано с помощью элементов данного множества называется множеством исходов данного опыта.

Обратимся за пояснением к примеру: пусть опыт состоит в бросании игрального кубика. Появление любого из 6 чисел на лицевой грани кубика можно рассматривать как исход, т. е. W={числа на лицевой грани кубика}={1; 2; 3; 4; 5; 6}. Пусть в этом опыте событие A состоит в появлении четного числа. Событие A может наступить при любом из 3-х исходов — 2, 4, 6.

Исходы, при которых изучаемое событие наступает, называются благоприятными исходами для данного события. Событие может быть выражено как множество благоприятных исходов. Говорят, что это множество служит математической моделью события. В приведенном примере событие

A= {2; 4; 6}.

Для множества элементарных событий существенно, что при реализации эксперимента G обязательно появляется какое-то из них, причем только одно (свойства полноты и попарной несовместности исходов).

Множество A является подмножеством множества исходов W, (A Ì W).

Достоверному событию соответствует множество W — ему благоприятны все исходы. Невозможное событие не имеет благоприятных исходов и выражается пустым множеством — Æ.

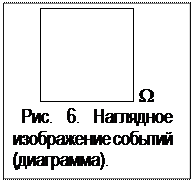
Итак, событие мы формально представляем как некоторое множество. Это позволяет применять алгебру множеств в выявлении связей между событиями. Отношения между событиями можно отобразить в наглядной форме на диаграмме Эйлера-Венна (рис. 6), показывая множество W прямоугольником, а событие А — фигурой внутри прямоугольника. Каждому исходу соответствует точка внутри прямоугольника. Точки внутри вложенной фигуры — исходы, благоприятные событию А. Исходы, находящиеся в незаштрихованной части прямоугольника образуют событие (не А), состоящее в непоявлении А. Событие 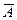называют дополнением события A или противоположным A событием.

На рис. 7 показана диаграмма для опыта с бросанием кубика. Здесь оказалось удобным изобразить исходы не точками, а долями прямоугольника. Область события А ={появление четного числа на лицевой грани} представлена кусочно — тремя частями.

Таблица 4.

Символика	Терминология	Иллюстрация (диаграмма)
в теории множеств	в теории вероятностей
W	Пространство, множество	Множество элементарных событий, достоверное событие
w, wÎ W	Элемент множества	Элементарное событие, исход	Точка в прямоугольнике
Æ	Пустое множество	Невозможное событие	—
	Множество A, подмножество множества W	Событие A.
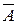
	Дополнение множества A до W	Противоположное событие (не A)
	Пересечение множеств A и B	Пересечение (одновременное появление) событий A и B
	Непересекающиеся множества	Несовместные события
	Объединение множеств (A или B)	Объединение, сумма событий
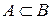
	A есть подмножество множества B	Появление события A влечет реализацию события B

В таблице 4 приведено соответствие теоретико-множественной терминологии и теории вероятностей и наглядное изображение наиболее распространенных случаев. Несовместные события не имеют общих благоприятных исходов, а также общих точек на диаграмме, у совместных — они есть. Совместные события выражаются пересекающимися множествами.

Уточним термины. Пересечением двухсобытий A и B называется событие, состоящее в одновременном их появлении. Объединением или суммой двух событий A и B называется событие, состоящее в появлении хотя бы одного из них.

Исчисление вероятностей основывается на следующих аксиомах, сформулированных А.Н. Колмогоровым:

1°. Каждому исходу w _i можно поставить в соответствие неотрицательное число p_i, называемое вероятностью;

2°. P (W) = 1 — вероятность достоверного события равна единице;

3°. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:

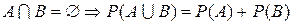. (10)

Аксиома 3° называется правилом сложения вероятностей. Правило можно распространить на любое число попарно несовместных событий. Из этой аксиомы вытекает важное следствие: вероятность случайного события равна сумме вероятностей всех благоприятных ему исходов. Таким образом, зная распределение вероятностей между исходами эксперимента, мы могли бы без труда найти вероятность любого связанного с ним события.

К сожалению, непосредственное вычисление вероятностей возможно только в классическом случае, когда все исходы опыта равновозможны, т. е. условия опыта обеспечивают равную возможность (вероятность) появления каждого из них.