
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
II.III.II. Классическое определение вероятности
|
|
Если все исходы опыта равновозможны, их называют шансами (случаями). Для опыта, сводящегося к системе n шансов, вероятность одного шанса равна 1/ n. Вероятность любого события А по правилу сложения равна сумме вероятностей благоприятных исходов. Нетрудно видеть, что она равна отношению числа m (A) шансов, благоприятных событию A, к числу n (W) всех шансов:
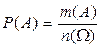 . (11)
. (11)
Пример. Бросается игральный кубик. Найти вероятность выпадения не менее трех очков.
Решение. W={числа на лицевой грани кубика}={1; 2; 3; 4; 5; 6}, n (W) = 6. В силу симметрии опыта исходы можно считать равновероятными, т. е. шансами.
Событие A= {появление не менее 3-х очков} = {3; 4; 5; 6}, m (A) = 4.
Искомая вероятность 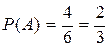 .
.
Решение задач:
- В урне 5 белых, 3 черных и 7 красных шаров. Найти вероятность того, что наугад вынутый из урны шар окажется: а) красным; б) белым.
- Из карточек сложено слово “ДОСТОПРИМЕЧАТЕЛЬНОСТИ”. С какой вероятностью ребенок выберет букву “О”?
- Куб покрасили, а затем распилили на маленькие кубики так, что каждое ребро оказалось поделенным на три доли. Найти вероятность того, что наудачу выбранный кубик не будет иметь окрашенных граней.
- Определить вероятность того, что наудачу взятая карта домино будет иметь оба поля одинаковые. В домино 28 карт, а на одном поле может быть не более 6 точек.
- С какой вероятностью в наудачу взятой карте домино хотя бы на одном поле будет пять очков?
- Найти вероятность того, что наугад взятая карта домино будет иметь сумму очков на полях не более 2.
- Известно, что дождь идет три дня подряд. С какой вероятностью: а) среда окажется дождливым днем; среда и четверг окажутся дождливыми?
- Определить вероятность того, что при бросании двух кубиков выпадет сумма: а)5 очков, б) не менее 5 очков?
- Из пяти букв разрезной азбуки составлено слово “КНИГА”. Неграмотный мальчик перемешал буквы, а потом наугад собрал их. Какова вероятность того, что он опять составил слово “КНИГА”?
- Какова вероятность того, что у случайного прохожего одинаковые инициалы фамилии, имени и отчества? Считать, что в инициалах не может быть букв ё, ъ, ы, ь.
- Из коробки с бильярдными шарами вынимают 2 шара. Какова вероятность того, что сумма их номеров не превосходит 7? Всего 16 шаров.
- Клякса падает на слово «осколок» и заливает две соседние буквы. С какой вероятностью будет залита буква «о»? С какой вероятностью будет залита буква «о» если клякса упала на слово «молоко»?
- Обезьяна печатает на пишущей машинке. Полагая, что машинка имеет только 33 клавиши, определите вероятность того, что обезьяна напечатает слово «банан» в результате 5 ударов.
- В коробке «Ассорти» 20 неразличимых по виду конфет, из которых 12 с шоколадной начинкой и 8 с фруктовой. Наудачу выбирают две конфеты. Какова вероятность того, что а) обе конфеты с шоколадной начинкой, б) обе с фруктовой, в) с разными начинками, г) чему равна сумма вероятностей в пунктах а) б) с)? Почему?