
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. По данным задачи выпишем вектор и матрицу и определим коэффициенты уравнения линейной регресии.
|
|
По данным задачи выпишем вектор и матрицу и определим коэффициенты уравнения линейной регресии.
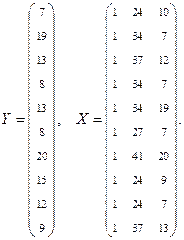
Тогда
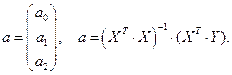
Найдем последовательно матрицу 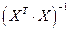 и вектор
и вектор 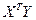 . Имеем
. Имеем

откуда
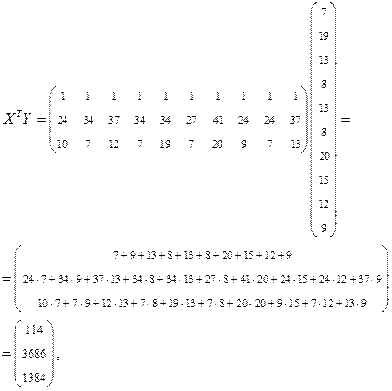
и, кроме того,
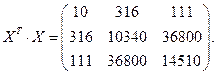
Теперь вычислим обратную матрицу 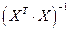 :
:
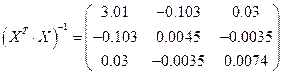 .
.
Теперь остается перемножить матрицу 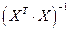 и вектор
и вектор 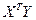 :
:
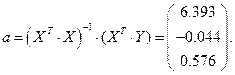
Таким образом, уравнение регрессии имеет вид:
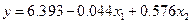 .
.
Найдем точечные характеристики всех имеющихся переменных.
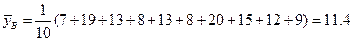 ,
,
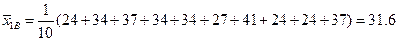 ,
,
 ,
,
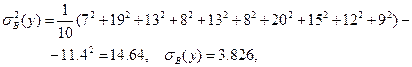
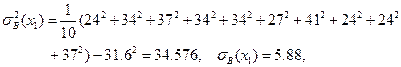
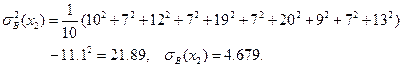
Теперь мы в состоянии определить коэффициент детерминации уравнения регрессии
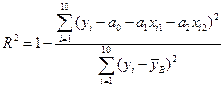 .
.
Вычислим сначала сумму
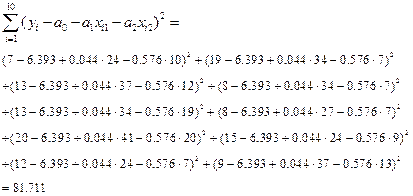 Отметим, что
Отметим, что
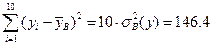 ,
,
откуда следует, что
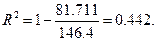
Коэффициент детерминации 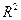 интерпретируется как доля изменения зависимой переменной, обусловленная изменением независимых переменных, то есть в нашем случае изменение
интерпретируется как доля изменения зависимой переменной, обусловленная изменением независимых переменных, то есть в нашем случае изменение  на 44.2% связано с изменением значений переменных
на 44.2% связано с изменением значений переменных 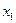 и
и 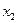 и на 55.8% со случайными факторами.
и на 55.8% со случайными факторами.
Чтобы проверить гипотезу о значимости уравнения регрессии на уровне значимости 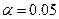 , воспользуемся критерием значимости
, воспользуемся критерием значимости
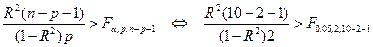 .
.
В нашем случае
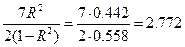 ,
,
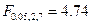 ,
,
и условие значимости не выполняется, что означает, что на выбранном уровне значимости гипотезы (когда мы хотим, чтобы вероятность ошибки первого рода была достаточно мала) экспериментальные данные позволяют считать, что на самом деле линейная часть уравнения регрессии равна нулю, и разброс значений переменной  связан только со случайными факторами.
связан только со случайными факторами.
Найдем стандартизированные регрессии и коэффициенты эластичности для каждой из объясняющих переменных. Имеем:
 ,
,
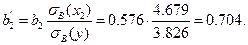
То, что выборочный коэффициент корреляции больше для переменной 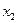 указывает, что в нашем примере второй параметр более тесно связан с независимой переменной, чем первый. Далее,
указывает, что в нашем примере второй параметр более тесно связан с независимой переменной, чем первый. Далее,
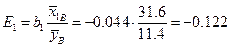 ,
,
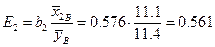 ,
,
откуда можно сделать вывод, что при увеличении величины 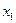 на 1% величина
на 1% величина  уменьшается на 12.2%, в то время как увеличение
уменьшается на 12.2%, в то время как увеличение 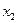 на 1% дает прирост
на 1% дает прирост  на 56.1%.
на 56.1%.
Найдем 95 %-ный доверительный интервал для коэффициентов регрессии. Нам потребуется точечная оценка параметра 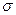 стохастической части зависимости случайной величины
стохастической части зависимости случайной величины  от
от 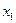 ,
, 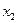 :
:
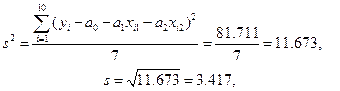
(сумма 81.711 в числителе этой формулы была найдена ранее при вычислении коэффициента детерминации 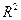 ).
).
Доверительные интервалы с доверительной вероятностью 0.95 для коэффициентов регрессии имеют вид
 для коэффициента
для коэффициента 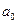 ,
,
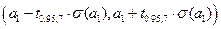 для коэффициента
для коэффициента 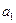 ,
,
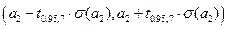 для коэффициента
для коэффициента 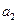 ,
,
где
 ,
,
элементы, стоящие на диагонали матрицы 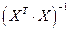 . Матрица
. Матрица 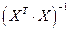 была ранее найдена в явном виде, поэтому
была ранее найдена в явном виде, поэтому
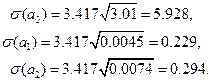
С учетом того, что 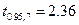 получаем три доверительных интервала для коэффициентов соответственно:
получаем три доверительных интервала для коэффициентов соответственно:
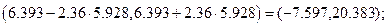
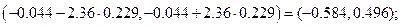
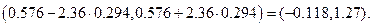
Определим теперь доверительные интервалы для среднего и индивидуального показателей значения себестоимости 1 т литья в цехах, в которых выработка литья на 1 рабочего составляет 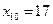 т, а брак литья -
т, а брак литья - 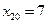 %. Формула для доверительного интервала для средних значений переменной имеет вид
%. Формула для доверительного интервала для средних значений переменной имеет вид
 ,
,
где
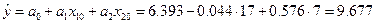 ,
,
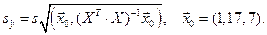
Поулчаем
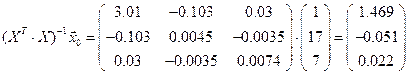
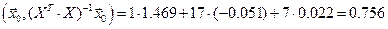 ,
,
откуда
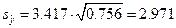 .
.
Тем самым доверительный интервал определен:
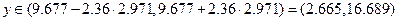 .
.
Для индивидуальных значений переменной  соответствующий доверительный интервал имеет вид:
соответствующий доверительный интервал имеет вид:
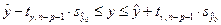 ,
,
где
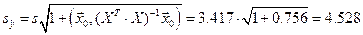 ,
,
откуда
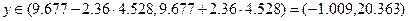
|