Пошаговые алгоритмы вычислений

Файл данных, который мы будем использовать в приводимых далее примерах, называется help.sav. Число объектов в этом файле равно 46, то есть N = 81. Ниже перечислены те переменные файла, которые мы будем использовать.

► помощь – зависимая переменная, интерпретируемая как время (в секундах) оказания помощи партнеру (среднее – 30, стандартное отклонение – 10);

► симпатия – оценка своей симпатии к партнеру, нуждающемуся в помощи (по 20-балльной шкале);

► агрессия – оценка своей агрессивности к партнеру (по 20-балльной шкале);

► польза – самооценка пользы от оказываемой помощи (по 20-балльной шкале);

► проблема – оценка серьезности проблемы своего партнера (по 20-балльной шкале);

► эмпатия – оценка эмпатии (склонности к сопереживанию) как результат тести­рования (по 10-балльной шкале).

Для проведения множественного регрессионного анализа сначала необходимо выполнить три подготовительных шага. Эти шаги (шаги 1-3) позволят подготовить рабочий файл данных, запустить программу IBM SPSS Statistics 19 и открыть файл (в данном случае – файл help.sav).

После завершения шага 3 на экране должно присутствовать окно редактора дан­ных со строкой меню и загруженным файлом help.sav.

Шаг 4. В меню Анализ выберите команду Регрессия ► Линейная. На экране по­явится диалоговое окно Линейная регрессия, показанное на рис. 1.

Рисунок 1 –Диалоговое окно Линейная регрессия (Linear Regression)

В верхней части диалогового окна расположено поле Зависимая переменная (Dependent), предназначенное для указания единственной переменной-критерия. Ниже следует список Независимые переменные (Independent(s)), заполняемый одной или несколькими независимы­ми переменными, число которых теоретически не ограничено. С помощью кнопки Следующий (Previous), расположенной справа от метки Блок 1 из 1, вы можете задать не один, а несколько наборов предикторов и тем самым провести одновременно несколько вариантов регрессионного анализа. Как только вы определите все независимые переменные и установите необходимые параметры анализа, щелчок на кнопке Сле­дующий (Previous) приведет к очистке списка Независимые переменные (Independent(s)), который будет готов к принятию нового набора предикторов. После того как вы зададите все блоки независимых переменных и щелкните на кнопке OK, SPSS выполнит все вариант регрессионного анализа и сгенерирует результаты для каждого из них. Обратите внимание, что во всех вариантах анализа, проводимых одновременно, должна быть общая зависимая переменная, иначе процедуру регрессии каждый раз пришлось бы запускать заново.

Важным элементом диалогового окна Линейная регрессия является раскрываю­щийся список Метод (Method). Пункты этого списка определяют алгоритмы включения не­зависимых переменных в уравнение регрессии.

► Принудительное включение (Enter) – метод, применяющийся по умолчанию. Все неза­висимые переменные включаются в уравнение независимо от степени их кор­реляции с переменной-критерием.

► Включение (Stepwise) – пошаговое включение переменных с проверкой на значимость их частной корреляции с критерием. В результате в уравнение включаются все пе­ременные, имеющие значимую частную корреляцию с переменной-критерием. Включение производится в порядке возрастания р-уровня.

► Исключение (Remove) – пошаговый метод, сначала включающий в уравнение регрессии все независимые переменные, а затем поочередно удаляющий все переменные, чья корреляция с критерием имеет уровень значимости выше заданного поро­гового значения. Как правило, пороговым значением является р = 0, 1.

► Шаговый отбор (Backward) – комбинация пошаговых методов включения и исключения. Основной идеей является изменение доли влияния независимой переменной на критерий при появлении в уравнении других независимых переменных. Если влияние какой-либо из включенных переменных становится слишком слабым, она исключается из уравнения. Подобный метод используется при регрессионном анализе наиболее часто.

► Блочное исключение (Forward) – это метод принудительного удаления переменных. Он требует предварительного задания метода Включение в качестве предыдущего блока, например Блок 1 из 1. При задании следующего блока, в данном случае Блок 2 из 2, в список Независимые переменные вы сможете ввести те независи­мые переменные, которые хотите исключить из уравнения регрессии. При вы­полнении команды вы получите результат со всеми заданными переменными, а затем – результат с удаленными переменными. Если в анализе участвуют не­сколько блоков, то можно задавать операцию удаления после каждого из них.

Окно и кнопка Переменная отбора наблюдений (Selection veriable) дадут возможность выбрать груп­пирующую переменную для задания подгруппы наблюдений, в отношении кото­рой будет проводиться анализ.

Кнопка Графики (Plots) используется для графического отображения остатков. Кнопка Статистики (Statistics) открывает диалоговое окно Линейная регрессия: Статистики (Linear Regression: Statistics), показанное на рис. 2. По умолчанию в окне установлены два флажка. Флажок Оценки (Estimates) вклю­чает в вывод коэффициенты В, стандартные коэффициенты регрессии β, а также соответствующие стандартные ошибки, t-критерии и уровни значимости. Флажок Согласие модели (Model fit) генерирует значения множественного коэффициента корреляции R, величину R², таблицу дисперсионного анализа, соответствующие F -величины и уровни их значимости. Таким образом, указанные флажки отвечают за генера­цию основных элементов регрессионного анализа.

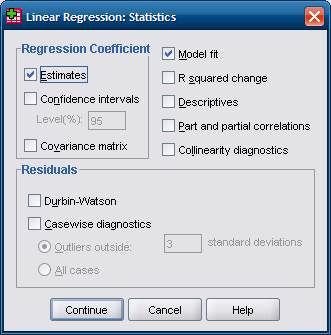
Рисунок 2 –Диалоговое окно Линейная регрессия: Статистики
(Linear Regression: Statistics)

Ниже пояснены наиболее важные флажки диалогового окна Линейная регрессия: Статистики.

► Доверительные интервалы (Confidence intervals) – включает в вывод для коэффициентов В довери­тельный интервал в 95 %.

► Матрица ковариаций (Covariance matrix) – генерирует таблицу, под главной диагональю которой расположены ковариаций, на главной диагонали – дисперсии, а над главной диагональю – корреляции.

► Изменение R-квадрата (R squared change) – для методов Включение и Шаговый отбор указывает изменения коэффициента R² при введении новых переменных в уравнение ре­грессии.

► Описательные статистики (Descriptives) – включает средние значения переменных, стандарт­ные отклонения, а также корреляционную матрицу.

► Диагностика коллинеарности (Collinearity diagnostics) – устанавливает наличие коллинеарностей (корреляций, близких к 1) между переменными.

Щелчок на кнопке Сохранить (Save) в диалоговом окне Линейная регрессия приводит к открытию диалогового окна Линейная регрессия: Сохранение, показанного на рис. 3. В нем имеется множество флажков, названия которых, как правило, представляют загадку даже для людей, искушенных в математике. Однако некото­рые весьма полезны.

Данное окно позволяет создать в файле данных новые переменные, содержащие значения, соответствующие установленным флажкам.

► В группе Предсказанные значения имеются 4 флажка. Флажок Нестандартизованные (Unstandardized) генерирует прогнозируемые значения, которые бывает полезно сравнить с фактическими значениями для оценки адекватности уравнения регрессии.

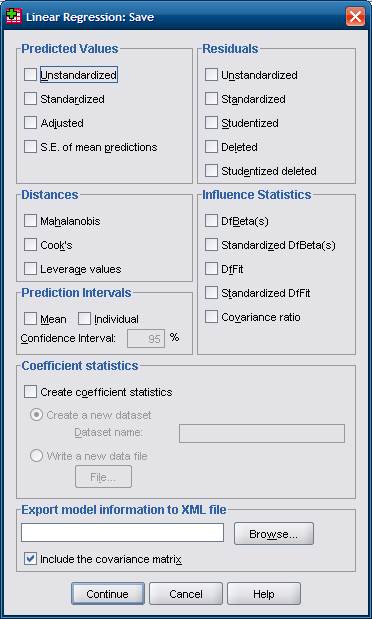
Кроме того, этот флажок позволяет получать прогнозы (оценки) зависимой переменной для тех объектов, для которых ее истинные значения неизвест­ны. Флажок Стандартизованные (Standardized) позволяет рассчитывать стандартизированные прогнозируемые значения (в z-значениях).

► В группу Остатки (Residuals) включены 5 флажков, позволяющих задавать сохраняемые значения остатков

► Флажки в группе Статистики влияния (Influence Statistics) позволяют исключать из выборки те или иные объекты. Так, если в команде спортсменов-бегунов один пробегает дистанцию гораздо хуже или гораздо лучше других, его результаты значи­тельно искажают статистические показатели всей команды. Иногда подоб­ные значения («выбросы») желательно исключать из анализа. К сожалению, подробное изложение этой процедуры выходит за пределы темы.

► С помощью поля и флажков из группы Интервалы предсказания (Prediction Intervals) можно изме­нять число процентов в доверительном интервале для средних или отдельных значений (по умолчанию – 95 %).

► Флажки в группе Расстояния (Distances) предоставляют три способа измерения расстоя­ния между объектами.

Наконец, рассмотрим диалоговое окно Линейная регрессия: Параметры (Linear Regression: Options), показанное на рис. 4. Это окно открывается при щелчке на кнопке Параметры (Options) в окне Ли­нейная регрессия.

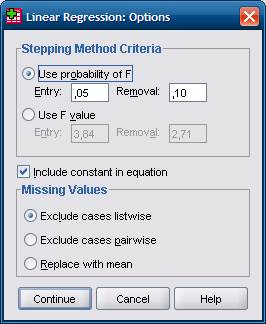
Флажок Включить в уравнение константу (Include constant in equation) установлен по умолчанию и без веских на то причин сбрасывать его не рекомендуется. Переключатели в группе Критерии ша­гового отбора (Stepping Method Criteria) позволяют управлять выполнением методов Включение, Исключение и Шаговый отбор. В поле Включение вы можете указать пороговую величину значи­мости для включения переменных в уравнение регрессии, а в поле Исключение для исключения переменных; в первом по умолчанию уставлено значение 0, 05, во втором – значение 0, 1. Группа переключателей Пропущенных значений (Missing Values) позволяет выбрать способ обработки отсутствующих значений.

Далее приведены два примера (шаги 5 и 5а), в первом из которых проводится множественный регрессионный анализ с участием зависимой переменной помочь и пяти предикторов симпатия, проблема, эмпатия, польза и агрессия. Для составле­ния уравнения регрессии мы воспользуемся установленным по умолчанию мето­дом Принудительное включение. Во втором примере мы используем некоторые из описанных выше параметров и пошаговый метод Шаговый отбор.

После выполнения шага 4 у вас должно быть открыто диалоговое окно Линейная регрессия, показанное на рис. 1.

Щелкните сначала на переменной помощь, чтобы выделить ее, а за­тем – на верхней кнопке со стрелкой, чтобы переместить перемен­ную в поле Зависимая переменная.

Щелкните сначала на переменной симпатия, чтобы выделить ее, а за­тем – на второй сверху кнопке со стрелкой, чтобы переместить пере­менную в список Независимые переменные.

Повторите предыдущее действие для переменных проблема, эмпатия, польза и агрессия.

Щелкните на кнопке ОК, чтобы открыть окно вывода.

В результате программа сгенерирует данные, показывающие, какая из независи­мых переменных оказывает наибольшее влияние на зависимую переменную.

В следующем примере мы проведем регрессионный анализ с участием тех же пере­менных, что и в предыдущем, однако будем использовать метод Шаговый отбор, включим в результат статистики для коэффициентов В, описательные статистики и характеристики модели.

После выполнения шага 4 должно быть открыто диалоговое окно Ли­нейная регрессия, показанное на рис. 1. Если вы уже успели порабо­тать с этим окном, очистите его щелчком на кнопке Сброс (Cancel) и выполните следующие действия.

1. Щелкните сначала на переменной помощь, чтобы выделить ее, а за­тем – на верхней кнопке со стрелкой, чтобы переместить перемен­ную в поле Зависимая переменная.

2. Щелкните сначала на переменной симпатия, чтобы выделить ее, а за­тем – на второй сверху кнопке со стрелкой, чтобы переместить пере­менную в список Независимые переменные.

3. Повторите предыдущее действие для переменных проблема, эмпатия, польза и агрессия.

4. В раскрывающемся списке Метод выберите пункт Шаговый отбор.

5. Щелкните на кнопке Статистики, чтобы открыть диалоговое окно Ли­нейная регрессия: Статистики, показанное на рис. 2.

6. Установите флажок Описательные статистики и щелкните на кнопке Продолжить, чтобы вернуться в диалоговое окно Линейная регрессия.

7. Щелкните на кнопке Сохранить, чтобы открыть диалоговое окно Линейная регрессия: Сохранить, показанное на рис. 3.

8. Установите флажок Нестандартизованные и щелкните на кнопке Про­должить, чтобы вернуться в диалоговое окно Линейная регрессия.

9. Щелкните на кнопке ОК, чтобы открыть окно вывода.

В результате выполнения приведенных выше инструкций будут сгенерированы данные, позволяющие судить о том, какая из независимых переменных оказывает наибольшее влияние на критерий. При составлении уравнения регрессии сначала в него включаются переменные, чья частная корреляция (β) с зависимой пере­менной имеет уровень значимости не выше 0, 05. Если затем обнаружится, что из включенных переменных какие-либо обнаруживают новый уровень значимости, превышающий значение 0, 1, они исключаются из уравнения. Кроме того, в резуль­тате выполнения процедуры будет создана переменная для хранения прогнози­руемых значений переменной помощь, рассчитанных по составленному уравнению регрессии. В окне вывода вы также сможете найти корреляционную матрицу для всех переменных и описательные статистики.

После выполнения шага 5 и шага 5а программа автоматически активизирует окно вывода. Для просмотра результатов при необходимости можно воспользоваться вертикальной и горизонтальной полосами прокрутки. Обратите внимание на стан­дартную строку меню в верхней части окна вывода: ее присутствие позволяет вы­полнять любые статистические операции, не переключаясь обратно в окно редак­тора данных.