
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Экономики (балансовый анализ)
|
|
Модель Леонтьева многоотраслевой
Цель балансового анализа — ответить на вопрос, возникающий в макроэкономике и связанный с эффективностью ведения многоотраслевого хозяйства: каким должен быть объем производства каждой из n отраслей, чтобы удовлетворить все потребности в продукции этой отрасли? При этом каждая отрасль выступает, с одной стороны, как производитель некоторой продукции, а с другой — как потребитель продукции и своей, и произведенной другими отраслями.
Связь между отраслями, как правило, отражается в таблицах межотраслевого баланса, а математическая модель, позволяющая их анализировать, разработана в 1936 г. американским экономистом В. Леонтьевым.
Предположим, что рассматривается п отраслей промышленности, каждая из которых производит свою продукцию. Часть продукции идет на внутрипроизводственное потребление данной отраслью и другими отраслями, а другая часть предназначена для целей конечного (вне сферы материального производства) личного и общественного потребления.
Рассмотрим процесс производства за некоторый период времени (например, год).
Введем следующие обозначения: xi — общий (валовой) объем продукции i -й отрасли (i = 1, 2,..., п);
xij — объем продукции i -й отрасли, потребляемой j -й отраслью в процессе производства (i, = 1, 2,..., п);
yi — объем конечного продукта i -й отрасли для непроизводственного потребления.
Так как валовой объем продукции любой i -й отрасли равен суммарному объему продукции, потребляемой п отраслями, и конечного продукта, то
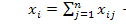 (i = 1, 2..... п). (2.14)
(i = 1, 2..... п). (2.14)
Уравнения (2.14) называются соотношениями баланса. Будем рассматривать стоимостный межотраслевой баланс, когда все величины, входящие в (2.14), имеют стоимостное выражение. Введем коэффициенты прямых затрат
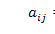
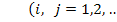 (2.15)
(2.15)
Показывающие затраты продукции  -й отрасли на производство единицы продукции
-й отрасли на производство единицы продукции  -й отрасли.
-й отрасли. 
Можно полагать, что в некотором промежутке времени коэффициенты  будут постоянными и зависящими от сложившейся технологии производства. Это означает линейную зависимость материальных затрат от валового выпуска, т.е.
будут постоянными и зависящими от сложившейся технологии производства. Это означает линейную зависимость материальных затрат от валового выпуска, т.е.
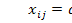
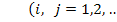 (2.16)
(2.16)
Вследствие чего построенная на этом основании модель межотраслевого баланса получила название линейной.
Теперь соотношение баланса (2.14) примут вид:
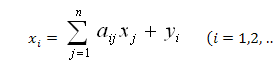 (2.17)
(2.17)
Обозначим:
 ,
,  ,
, 
Где X- вектор валового выпуска, Y- вектор конечного продукта, A- матрица прямых затрат (технологическая или структурная матрица).
Тогда систему (2.14) можно записать в матричном виде:
X=AX+Y. (2.18)
Основная задача межотраслевого баланса состоит в отыскании такого вектора валового выпуска X, который при известной матрице прямых затрат A обеспечивает заданный вектор конечного продукта Y.
Перепишем уравнение (2.18) в виде:
(E-A)X=Y. (2.18)
Если матрица (Е-А) невырожденная, т.е. |Е-А|≠ 0, то по формуле (2.7)
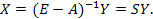 (2.20)
(2.20)
Матрица 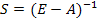 называется матрицей полных затрат.
называется матрицей полных затрат.
Чтобы выяснить экономический смысл элементов матрицы 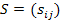 , будем задаваться единичными векторами конечного продукта1
, будем задаваться единичными векторами конечного продукта1 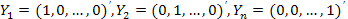 . Тогда по формуле (2.20) соответствующие векторы валового выпуска будут
. Тогда по формуле (2.20) соответствующие векторы валового выпуска будут
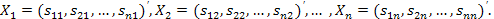
Следовательно, каждый элемент 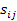 матрицы S есть величина валового выпуска продукции i -й отрасли, необходимого для обеспечения выпуска единицы конечного продукта j -й отрасли
матрицы S есть величина валового выпуска продукции i -й отрасли, необходимого для обеспечения выпуска единицы конечного продукта j -й отрасли 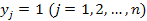 .
.
В соответствии с экономическим смыслом задачи значения 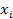 должны быть неотрицательны при неотрицательных значениях
должны быть неотрицательны при неотрицательных значениях 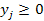 и
и 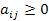 , где
, где 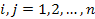 .
.
Матрица А≥ 0 называется продуктивной, если для любого вектора Y≥ 0 существует решение Х≥ 0 уравнения (2.19). В этом случае и модель Леонтьева называется продуктивной.
Существует несколько критериев продуктивности матрицы А. Один из них говорит о том, что матрица А продуктивна, если максимум сумм элементов ее столбцов не превосходит единицы, причем хотя бы для одного из столбцов сумма элементов строго меньше единицы, т.е. матрица А продуктивна, если 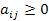 для любых
для любых 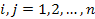 и
и 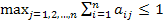 , и существует номер j такой, что
, и существует номер j такой, что 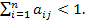
1 Используем для кратности знак транспонирования матрицы – «штрих».
Пример 2.10. В таблице приведены данные об исполнении баланса за отчетный период, усл. ден. ед.:
| Отрасль | Потребление | Конечный продукт | Валовой выпуск | |||
| энергетика | машино- строение | |||||
| Производство | Энергетика Машиностро- строение | |||||
Вычислить необходимый объем валового выпуска каждой отрасли, если конечное потребление энергетической отрасли увеличится вдвое, а машиностроительной сохраниться на прежнем уровне.
Решение. Имеем x1=100, x2=150, x11=7, x12=21, x21=12, x22=15; y1=72, y2=123. По формуле (2.15) находим коэффициенты прямых затрат:
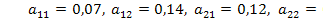 , т.е. матрица прямых затрат A=
, т.е. матрица прямых затрат A= 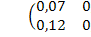 имеет неотрицательные элементы и удовлетворяет критерию продуктивности:
имеет неотрицательные элементы и удовлетворяет критерию продуктивности:
max{0, 07+0.12; 0, 14+0, 10}=max{0, 19; 0, 24}=0, 24< 1.
Поэтому для любого вектора конечного продукта Y можно найти необходимый объем валового выпуска X по формуле (2, 20):
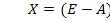 .
.
Найдем матрицу полных затрат 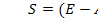 :
:
E - A= 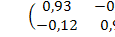 . Так как | E - A |=0, 8202≠ 0, по формуле (1.14)
. Так как | E - A |=0, 8202≠ 0, по формуле (1.14)
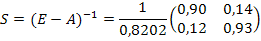
По условию вектор конечного продукта 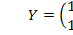 . Тогда по формуле (2.17) получаем вектор валового выпуска:
. Тогда по формуле (2.17) получаем вектор валового выпуска:
 , 1/6 – в банк 2 и 1.3 вкладка – в банк 3, то сумма вкладов в конце года составила бы вновь 7250 ден. ед. Какой процент выплачивает каждый банк?
, 1/6 – в банк 2 и 1.3 вкладка – в банк 3, то сумма вкладов в конце года составила бы вновь 7250 ден. ед. Какой процент выплачивает каждый банк?