Галлямова Р.Ф.

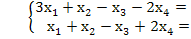
Решение.

Для системы из m уравнений с n неизвестными (m < = n) любые m переменных называются базисными, если определитель составленный из коэффициентов при этих неизвестных отличен от нуля (остальные n – m переменных называются свободными).

Система состоит из m=2 уравнений с n=4 неизвестными

Определим различные решения этой системы. Количество базисных решений не должен превышать 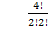. По определению базисное решение включает только две переменные, предполагая, что небазисных нулевых переменных 2.

I. Нулевые (небазисные) переменные: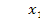

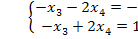
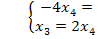
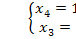
Единственное решение, 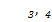=> доступно базисное решение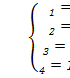

II. Нулевые (небазисные) переменные:

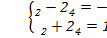
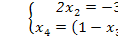
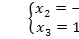
Единственное решение, 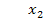=> недоступно базисное решение.

III. Нулевые (небазисные) переменные: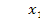

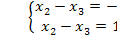
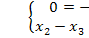
Решение нет => базисного решения не существует.

IV. Нулевые (небазисные) переменные: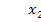

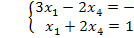
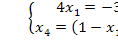
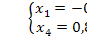
Единственное решение, 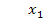=> недоступно базисное решение.

V. Нулевые (небазисные) переменные: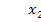

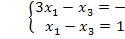
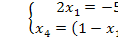
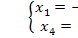
Единственное решение, 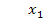=> недоступно базисное решение.

VI. Нулевые (небазисные) переменные: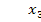

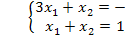
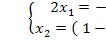
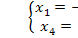
Единственное решение, 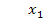=> недоступно базисное решение.