
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Перпендикулярные прямые
|
|
Две прямые перпендикулярны в том и только в том случае, если через каждую из них можно провести плоскость, перпендикулярную к другой прямой.
На рис. 71 изображена прямая l общего положения, к которой требуется провести перпендикулярную прямую.
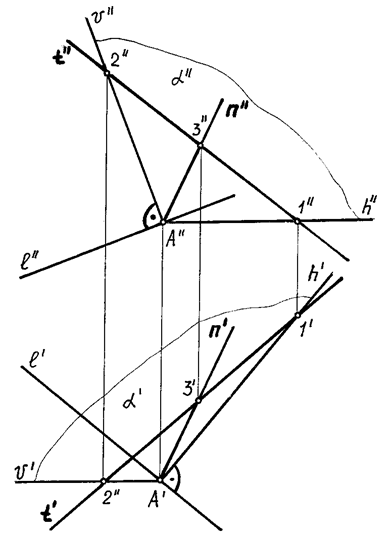
Рис. 71
Через точку А прямой l строим перпендикулярную к ней плоскость a (h ´ v):
l' ^ h'; l'' ^ h'' (рис. 71).
Любая прямая, лежащая в плоскости a будет также перпендикулярна к данной прямой l. Поэтому проведем в этой плоскости произвольную прямую t, на которой возьмем произвольную точку, например, точку В (рис. 71).
Соединив точки А и В, лежащие в плоскости, получим прямую n, перпендикулярную к данной прямой l (рис. 71).
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1) Что называется линией наибольшего наклона плоскости?
2) Как определить угол наклона плоскости к фронтальной плоскости проекций?
3) Как отображается на комплексном чертеже взаимная перпендикулярность прямой и плоскости?
Сформулировать необходимые и достаточные условия перпендикулярности двух прямых общего положения.
5) При каких условиях перпендикулярны между собой две плоскости общего положения?
6) Как провести плоскость, перпендикулярную к данной прямой?
7) Как провести перпендикуляр из точки на прямую общего положения?
8) Как построить взаимно-перпендикулярные плоскости?
7. ПОСТРОЕНИЕ ТЕНЕЙ
План:
7.1. Основы теории теней
7.2. Тени от точки, линии и плоской фигуры
7.3. Тень, падающая от одной фигуры на другую
7.4. Тени геометрических тел
7.5. Тени пересекающихся многогранников (от здания)
7.6. Тени на фасадах зданий