В общем случае поиск оптимальных параметров сводится к решению нелинейной экстремальной задачи. Обычно рассматривают линейный случай

План лекции

1. Общий вид однофакторной регрессионной модели

2. Метод наименьших квадратов

3. Оценка качества уравнения регрессии

4. Нелинейные регрессионные модели

5. Содержательная интерпретация параметров регрессии

1. Простейшие регрессионные модели отражают взаимосвязь показателя только с одним фактором. В общем случае однофакторную регрессионную модель можно представить в виде

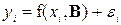, (1.1)

где

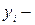значение 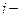ого наблюдения моделируемого показателя;

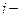значение фактора в ом наблюдении;

вектор неизвестных параметров, которые оцениваются по статистическим данным;

функция определяющая структуру регрессионной модели (линейную, степенную и т.п.);

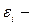ненаблюдаемая случайная величина, представляющая собой ту часть вариации показателя , которая не объясняется соответствующими изменениями фактора .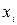

Чем ниже уровень возможных значений случайной величины 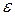, тем точнее модель отражает взаимодействие фактора х с показателем y. Т.е. параметры модели должны подбираться таким образом, чтобы минимизировать сумму квадратов отклонений (случайных составляющих )

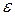. (1.2)

В общем случае поиск оптимальных параметров сводится к решению нелинейной экстремальной задачи. Обычно рассматривают линейный случай

, (1.3)

который значительно упрощает решение этой задачи.

2. Рассмотрим применение метода наименьших квадратов к случаю построения линейной регрессии (1.3). Для этого случая (1.2) перепишется в виде

. (2.1)

Применяя дифференциальное исчисление для минимизации (2.1) и дифференцируя по и 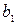, получаем систему линейных уравнений

,

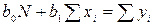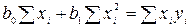. (2.2)

Разделив левую и правую части этой системы на число наблюдений N и произведя замену:

; ; ; ,

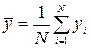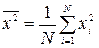перепишем систему (2.2) в виде:

,

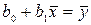. (2.3)