Целочисленные модели

Результаты решений многих задач, стоящих перед строителями, должны быть выражены в целых числах (например, определение оптимального количества заводов, являющихся поставщиками строительных конструкций или числа монтажных кранов и т.д.). Но если даже в простую задачу линейного программирования внести дополнительное требование целочисленности неизвестных (х = 1, 2, 3 и т.д.), то решать ее обычными методами уже нельзя. На первый взгляд кажется, что можно легко выйти из положения, округлив полученное каким-либо методом решение. Но, что может означать, к примеру, 2, 3 дома? Надо строить 3 дома? Это решение невозможно, либо возможно осуществить за счет уменьшения других показателей плана. Найти целочисленный оптимальный план - задача непростая. Для решения ее требуется применение довольно тонких специальных математических методов (например, метод " Гомори", основанный на идеях симплекс-метода).

Одним из примеров целочисленного программирования является задача о назначениях. Покажем на примере сущность этой задачи и алгоритм ее решения, в основе которого лежит так называемый венгерский метод.

Пример. Пусть имеется необходимость перебросить пять строительных бригад к месту строительства пяти различных объектов. Под назначением понимается факт приписки бригады к одному из объектов. Задача состоит в том, чтобы найти такое назначение, при котором общее время доставки бригад к месту работы было минимальным.

Представим время t_ij доставки i-ой бригады в j-ый пункт назначения в виде таблице 17.

Таблица 17 – Этап 1 Таблица 18 – Этап 2

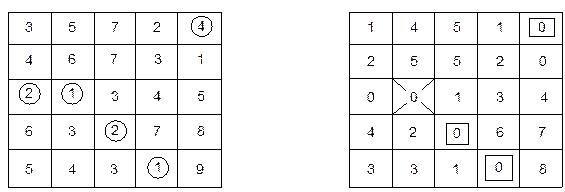
Основной принцип задачи о назначениях состоит в следующем: оптимальность решения не нарушается при уменьшении (увеличении) элементов t_ij строки (или столбца) таблицы (матрицы) на одну и ту же величину t.

Алгоритм решения может быть представлен в виде этапов.

Этап 1.Образование нулей.

Среди элементов каждого столбца таблицы 17 выбирается наименьший элемент (в таблице эти элементы обведены кружочками) и вычитается из всех элементов этого столбца. В результате этих действий получаем таблицу 18, в которой элементами являются разности

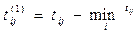(6.24)

Таблица 19 – Этап 3 Таблица 20 – Этап 4

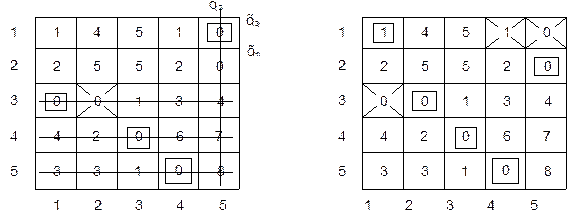
Этап 2. Поиск возможного оптимального решения.

Оптимальное решение в данной постановке означает, что затраты имеют нулевое значение. Если такое решение найти не удалось, то следует перейти к третьему этапу. Последовательность действий при поиске оптимального решения состоит в следующем. Анализ таблицы 18 начинается с выявления строк, содержащих минимальное число нулей, при этом один из нулей такой строки обводится квадратиком. Затем вычёркиваются все остальные нули, находящиеся в этой строке. Процесс продолжается до тех пор, пока в таблице все нули будут либо обведены квадратиками, либо вычеркнутыми. На данном этапе оптимального решения получить не удалось, так как во второй строке таблицы нет нулевого элемента.

Возьмем, например, элемент t₂₂ - 5, тогда решение будет иметь вид:

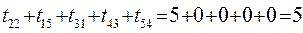(6.25)

Это решение неоптимально (таблица 19).

Этап 3. Образование набора строк и столбцов, содержащих все нули, имеющиеся в таблице (таблица 19).

Последовательность действий.

1 Пометим крестиком (х) строки, не содержащие ни одного обведённого квадратиком нуля. В нашем случае строка 2.

2 Отметим каждый столбец, содержащий зачеркнутый нуль хотя бы в одной из помеченных строк. В нашем случае 5-ый столбец.

3 Пометим каждую строку, в которой содержится обведенный квадратиком нуль хотя бы в одном из помеченных столбцов. В нашем случае строка 1.

4 Далее повторяем перечисленные действия 2 и 3 пока не останется строк и столбцов, которые еще можно пометить. Переходим к этапу 4.

Этап 4. Завершение этапа 3.

Прочеркнем каждую непомеченную строку и каждый помеченный столбец (таблица 19). Прочеркнем строки 3, 4, 5 и 5-ый столбец. Переходим к этапу 5.

Этап 5. Добавление нулей.

В части таблицы, состоящей из неперечеркнутых элементов, выберем наименьший элемент (таблица 19). Это будет элемент 1-ой строки, равный 1. Вычтем этот элемент из всех элементов столбцов 1, 2, 3, 4, 5 и прибавим его затем ко всем элементам перечеркнутых строк, т.е. строк 3, 4, 5. В результате получаем таблицу 20.

Этап 6. Получение оптимального решения или переход к этапу 3.

Оптимальное решение определяется в последовательности, описанной в этапе 2. Повторив этап 2, получим таблицу 20. В таблице 20 нули, обведенные квадратиками, образуют оптимальное решение:

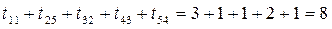(6.26)