Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Примерные тесты. Динамическое программирование
|
|
Практическая работа
Тема: «Динамическое программирование»
Содержание
Задание 1. Оптимальное распределение ресурсов. 1
Задание 2. Планирование минимальных затрат на перспективу. 2
Вопросы для самоконтроля. 3
Примерные тесты. Динамическое программирование. 3
Задание 1. Оптимальное распределение ресурсов
На авторемонтном предприятии имеются 7 цехов ремонта автомобилей. Известно, что i – й цех ( i =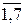 
), получив х единиц комплектов запчастей, отремонтирует φ i (х ) единиц автомобилей (табл. 12).
Требуется распределить А (А=7) единиц комплектов запчастей между указанными пятью (таблица 13) постами предприятия так, чтобы общее количество отремонтированных ими автомобилей было максимальным.
Таблица 12
Исходная информация
| Х ед. φ i (х) усл. ед. | |||||||
| φ 1(х) | |||||||
| φ 2(х) | |||||||
| φ 3(х) | |||||||
| φ 4(х) | |||||||
| φ 5(х) | |||||||
| φ 6(х) | |||||||
| φ 7(х) |
Таблица 13
Варианты заданий
| № варианта | Цехи ремонта |
| 1, 2, 3, 5, 7 | |
| 1, 3, 4, 5, 7 | |
| 2, 1, 4, 5, 6 | |
| 3, 4, 5, 6, 7 | |
| 4, 5, 6, 7, 3 | |
| 3, 5, 6, 4, 7 | |
| 4, 3, 2, 7, 6 | |
| 5, 4, 3, 7, 1 | |
| 1, 2, 3, 4, 5 | |
| 2, 3, 4, 5, 7 | |
| 1, 2, 3, 6, 7 | |
| 1, 3, 6, 5, 7 | |
| 2, 3, 4, 7, 6 | |
| 2, 6, 5, 4, 7 | |
| 3, 7, 6, 2, 1 | |
| 1, 2, 7, 6, 4 | |
| 2, 1, 5, 6, 4 | |
| 3, 2, 5, 6, 7 | |
| 1, 2, 3, 4, 5 | |
| 2, 3, 4, 5, 6 | |
| 3, 4, 2, 1, 6 | |
| 5, 6, 7, 4, 3 | |
| 2, 3, 4, 7, 5 | |
| 6, 7, 5, 3, 4 | |
| 4, 5, 6, 3, 1 | |
| 1, 2, 5, 4, 7 | |
| 2, 7, 6, 5, 4 | |
| 3, 4, 6, 7, 5 | |
| 2, 6, 7, 5, 3 | |
| 7, 6, 5, 1, 2 |
Задание 2. Планирование минимальных затрат на перспективу
Пусть необходимо удовлетворить потребность Q в некотором виде продукции. Для этого существуют действующие предприятия с мощностью Ni, но они не в состоянии полностью обеспечить всю потребность. Возникает вопрос о строительстве новых предприятий и расширении или реконструкции старых. Известны затраты на расширение старых предприятий (табл. 14) и строительство новых (табл. 15). Требуется выбрать оптимальный вариант строительства объектов таким образом, чтобы с минимальными затратами удовлетворить потребность в продукции.
Таблица 14
Затраты (ден. ед.) на расширение действующих предприятий
| Мощность предприятия (тыс.т) Номер действующего предприятия | ||||||
| - - - - - | - - | - - |
Таблица 15
Затраты (ден. ед.) на строительство новых предприятий
| Мощность предприятий (тыс.т) Номер предприятия | |||||
| - - - | - - - |
Таблица 16
Варианты заданий
| № варианта | Q потребность (тыс. т) | Ni – мощность i- ого действующего предприятия (тыс.т) | Предприятия | |||||
| N1 | N2 | N3 | N4 | N5 | действующие | новые | ||
| 1, 5 2, 4 3, 5 1, 2 1, 3 2, 3 2, 5 3, 4 1, 4 1, 5 2, 4 3, 5 1, 2 1, 3 2, 3 2, 5 3, 4 1, 4 1, 5 2, 4 3, 5 1, 2 1, 3 2, 3 2, 5 3, 4 1, 4 1, 5 2, 4 3, 5 | 1, 2, 3 1, 2, 4 1, 3, 4 1, 2, 5 1, 3, 4 2, 3, 4 1, 3, 5 2, 3, 5 3, 4, 5 3, 4, 5 2, 3, 5 1, 3, 5 2, 3, 4 1, 3, 4 1, 2, 5 1, 3, 4 1, 2, 4 1, 2, 3 1, 2, 4 1, 3, 4 1, 2, 5 1, 3, 4 2, 3, 4 1, 3, 5 2, 3, 5 3, 4, 5 2, 3, 5 1, 3, 5 2, 3, 4 1, 3, 4 |
Вопросы для самоконтроля
1. Особенности задач, решаемых методом динамического программирования (ДП).
2. Каков смысл функции Беллмана в задаче оптимального распределения ресурсов?
3. Зачем составляется функциональное уравнение Беллмана?
4. Какова суть принципа оптимальности, положенного в основу вывода функционального уравнения Беллмана в задаче оптимального распределения ресурсов?
5. Что является исходной информацией для задачи оптимального распределения ресурсов?
Примерные тесты. Динамическое программирование
1. Динамическое программирование применяют для решения задач:
а) дискретных; б) блочных; в) дробно-линейных;
г) оптимизационных, связанных с многошаговыми процессами.
2. Основной принцип метода динамического программирования:
а) разработка управленческого решения;
б) введение функции Беллмана;
в) если на первом шаге принято решение, то дальнейшее решение должно приниматься таким образом, чтобы за оставшееся число шагов достичь максимального (минимального) результата.
3. Смысл функции Беллмана:
а) максимальная прибыль; б) минимальные затраты;
в) максимальная эффективность многошагового процесса, состоящего из к шагов;
г) максимальное количество продукции.
4. Математическая модель задачи:
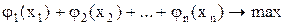
при ограничениях:
х1+х2+…+хn = А
хj ≥ 0, j=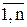 
является моделью (указать соответствие программирования), если функции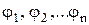 
заданы
| а) линейного б) нелинейного в) динамического | 1) таблично 2) дробно-линейные 3) нелинейные |
5. При решении задачи о распределении ресурсов смысл функции Беллмана fk (x):
а) максимальное количество продукции, которое может выпустить одно k-тое предприятие;
б) максимальное количество продукции, которое могут выпустить к предприятий, когда между ними распределено х единиц ресурса;
в) максимальное количество продукции, которое могут выпустить к предприятий, когда k-му предприятию выделено х единиц ресурса.
6. В задаче об оптимальном распределении ресурсов смысл выражения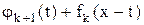 
:
а) k+1 – е предприятие, получив 0 ≤ t ≤ x единиц ресурса, выпускает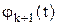 
единиц продукта;
б) на долю первых k предприятий остается x – t единиц ресурса;
в) общий выпуск продукции k+1 – м предприятиями, когда k+1 – му выделено t единиц ресурса и остатки (x – t) остальным k предприятиям.
7. Для проверки правильности расчетов (самоконтроль) находят количество:
а) общих ресурсов;
б) выпускаемой продукции каждым предприятием при распределении ресурсов между ними по исходной информации;
в) суммарной выпускаемой продукции всеми предприятиями при данном распределении ресурса между ними по исходной информации.
8. При планировании удовлетворения потребности с минимальными затратами на перспективу методом динамического программирования функция Беллмана fi(x) имеет смысл:
а) минимальные затраты на удовлетворение x единиц потребности по i- му варианту;
б) минимальные затраты максимального удовлетворения потребности;
в) минимальные затраты удовлетворения потребности в x единиц за счет расширения действующего предприятия и строительства i новых.
9. Удовлетворить потребность региона в 100 ед. продукта можно за счет двух действующих предприятий и трех новых, но тогда min затраты составят:
а)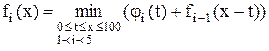 
;
б)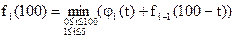 
;
в)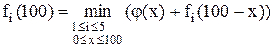 
.
10. Смысл функции Беллмана f4(500) задачи планирования минимальных затрат на перспективу:
а) минимальные затраты на удовлетворение 500 единиц потребности по четвертому варианту, т.е. за счет четвертого предприятия;
б) минимальные затраты на удовлетворение 500 единиц потребности за счет всех четырех предприятий;
в) затраты на удовлетворение потребности в 500 единицах продукта всеми четырьмя предприятиями.
|