Задание объектов в проекциях с числовыми отметками

ПРОЕКЦИИ С ЧИСЛОВЫМИ ОТМЕТКАМИ

Методические указания

к выполнению графической работы

Волгоград 2004

УДК 515.181.25 (076.5)

Проекции с числовыми отметками: Методические указания к выполнению графической работы / С. Н. Торгашина, Л.А. Иванова. - Волгоград: ВолгГАСУ, 2004, -44 с.

Методические указания содержат необходимые материалы для выполнения графической работы по курсу начертательной геометрии.

Для студентов 1 курса специальностей ОБД, АД, ЭУДХ, ПРХД, Арх.

Ил. 37. Библиогр. 5 назв.

Прил. I, 2, 3.

ЦЕЛЬ РАБОТЫ

Предполагается, что выполнение данной графической работы позволит студенту:

-изображать земную (топографическую) поверхность в виде планов;

-изображать инженерные земляные сооружения на топографической по­верхности;

-решать инженерные задачи по определению границ земляных работ на строительных площадках;

-строить профиль топографической поверхности и инженерного соору­жения.

СОДЕРЖАНИЕ И ОФОРМЛЕНИЕ РАБОТЫ

При выполнении работы решается задача определения границы земляных работ, откосов площадки и дороги, строится профиль сооружения по указан­ному направлению.

Работа выполняется в карандаше на листе формата A3 по индивидуаль­ным заданиям (прил. 1, 2). Основная надпись по ГОСТ 2.104-68 (форма 1). Наименование чертежа «Проекции с числовыми отметками». Оформление чертежа в соответствии с ГОСТ 2303-68, 2.304-81, 2.307-68. Масштаб черте­жа М 1-200. Образец выполнения работы в прил.З.

ОБЩИЕ СВЕДЕНИЯ О ПРОЕКЦИЯХ С ЧИСЛОВЫМИ ОТМЕТКАМИ

Применение в строительстве

Метод проекций с числовыми отметками находит широкое применение при изображении топографической поверхности и при проектировании раз­личных земляных сооружений, когда высота изображаемого объекта значи­тельно меньше его длины и ширины. К таким объектам относятся шоссей­ные и железные дороги, аэродромы, гидротехнические и др. сооружения.

Задание объектов в проекциях с числовыми отметками

Сущность метода проекции заключается в том, что объект ортогонально проецируется на одну горизонтальную плоскость проекций По - плоскость нулевого уровня. При этом для однозначного задания рядом с точками, опре­деляющими объект, (справа) пишут числа, указывающие расстояния (обычно в мм) от данных точек до плоскости нулевого уровня. Эти числа и называются числовыми отметками. Перед числовой отметкой ставят знак минус, ес­ли точка расположена ниже плоскости нулевого уровня (рис. 1).

А

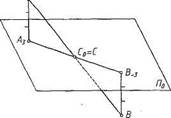
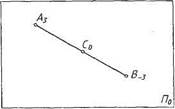
Рис.1 Рис.2

Для получения изображения объекта в проекциях с числовыми отметками плоскость нулевого уровня с проекциями точек совмещают с фронтальной плоскостью проекций. Такой чертеж в топографическом черчении называют планом. Для решения задач и изображения объектов на планах необходимо задавать линейный масштаб (рис. 2).

Длина горизонтальной проекции отрезка прямой называется заложением (L). Разность концов отрезка прямой называется подъемом, или превышением (h).

Тангенс угла наклона прямой к плоскости нулевого уровня называется уклоном прямой (i). Уклоном отрезка прямой можно считать отношение превышения к заложению.

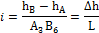
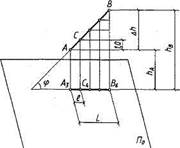
Рис.3

В

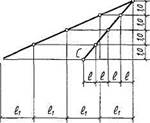
Рис.4

Если разность отметок двух точек прямой равна единице (АС), то заложе­ние отрезка прямой, определяемой этими точками (АзС4), называется интервалом (l). Другими словами, интервалом прямой является заложение, соответствующее единице подъема (рис. 3)

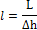
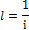
Интервал и уклон - величины, обратные друг другу. Из этого следует, что чем больше уклон прямой, тем меньше интервал и наоборот (рис. 4).

Угол, заключенный между отрезком прямой и заложением, называется углом наклона прямой к плоскости нулевого уровня (φ).

Интервалом приходится пользоваться при градуировании проекции пря­мой линии.

Проградуировать проекцию прямой значит определить на ней точки с по­стоянной разностью отметок, равной единице.

L

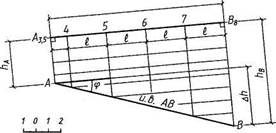
Рис.5

При первом способе градуирования (рис. 5) определяют полную харак­теристику отрезка прямой, т.е. интервал, угол наклона, истинную длину от­резка. Пусть задана проекция отрезка прямой А₃, ₅В₈ и масштаб чертежа. Для решения задачи необходимо из концов проекций точек А и В провести про­ецирующие лучи перпендикулярно проекции АВ. В заданном масштабе от­ложить расстояние от А и В до плоскости нулевого уровня, за единицу пре­вышения приняв 1м. Полученный отрезок есть истинная величина АВ.

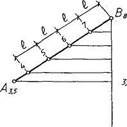
При втором способе градуирования (рис. 6) используют метод пропор­ционального деления отрезка в заданном отношении. Для этого из любого конца проекции отрезка проводится прямая под произвольным углом к нему. На этой прямой в заданном масштабе откладывают последовательно превы­шения между концевыми точками отрезка, отмечая каждую единицу длины. Соединив крайние точки отрезков прямой линией, проводим параллельно ей прямые через точки деления, определяя интервал на проекции АВ.

Рис.6

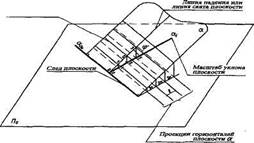
Задание плоскости масштабом уклона является наиболее наглядным и удобным в проекциях с числовыми отметками. Масштабом уклона плоско­сти называется градуированная проекция линии наибольшего наклона (ската) плоскости. Эта линия проводится перпендикулярно горизонталям плоскости.

На рис.7 изображена плоскость £ с горизонталями 0, 1, 2, 3 и линией наи­большего наклона 0-3. Превышения горизонталей равны 1м.

φ - угол падения плоскости, или угол наклона плоскости £ к плоскости нулевого уровня, заключен между линией наибольшего ската и проекцией этой линии на плоскость нулевого уровня. Следовательно, масштаб уклона плоскости — проградуированная проекция линии наибольшего ската плоско­сти (рис. 8). Задание плоскости масштабом уклона на плане, и угол падения плоскости (рис. 9).

Рис.8

На рис.9 плоскость задана тремя точками. Нужно задать эту плоскость масштабом уклонов и определить угол падения плоскости.

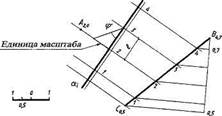
Рис.9

Для решения задачи необходимо проградуировать отрезок прямой, со­единяющий минимальную и максимальную отметки точек (ВС) в заданном масштабе. Провести горизонталь с отметкой А₂, ₀ и другие горизонтали в точ­ках градуирования отрезка ВС. Провести масштаб уклона плоскости £ пер­пендикулярно горизонталям и проградуировать его. Угол падения плоскости определяется как тангенс φ, где одним катетом является интервал плоскости, другим - единица длины масштаба.