
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Остатки, Стандартизированные остатки, График остатков, График подбора, График нормальной вероятности
|
|
Флажок против указанных опций не ставят на этапе предварительных расчетов, поскольку предварительный анализ проводят по итогам расчетов, приведенных в таблице. При повторных уточненных расчетах эти опции могут оказаться полезными для того, чтобы вычислить остатки, построить диаграмму остатков для каждой независимой переменной, график.
После щелчка на ОК в отдельном листе появятся результаты предварительных расчетов в виде табл.2.
Таблица 2
Выводимые программой Microsoft Excel результаты предварительных расчетов коэффициентов регрессии, регрессионной статистики и дисперсионного анализа
| Регрессионная статистика | ||||||||
| Множественный R | 0, 998893 | |||||||
| R-квадрат | 0, 997788 | |||||||
| Нормированный R-квадрат | 0, 992258 | |||||||
| Стандартная ошибка | 0, 002129 | |||||||
| Наблюдения | ||||||||
| Дисперсионный анализ | ||||||||
| df | SS | MS | F | Значимость F | ||||
| Регрессия | 0, 004088 | 0, 000818 | 180, 4229 | 0, 005521 | ||||
| Остаток | 9, 06E-06 | 4, 53E-06 | ||||||
| Итого | 0, 004097 | |||||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95, 0% | Верхние 95, 0% | |
| Y-пересечение | -1, 40707 | 0, 219814 | -6, 40118 | 0, 023546 | -2, 35285 | -0, 46129 | -2, 35285 | -0, 46129 |
| Т | 0, 006185 | 0, 000636 | 9, 732943 | 0, 010392 | 0, 003451 | 0, 00892 | 0, 003451 | 0, 00892 |
| C | -0, 00187 | 0, 001448 | -1, 29021 | 0, 326024 | -0, 0081 | 0, 004361 | -0, 0081 | 0, 004361 |
| n | -0, 04395 | 0, 009819 | -4, 4756 | 0, 04647 | -0, 0862 | -0, 0017 | -0, 0862 | -0, 0017 |
| V | 5, 81E-05 | 3, 09E-05 | 1, 880342 | 0, 200808 | -7, 5E-05 | 0, 000191 | -7, 5E-05 | 0, 000191 |
| P | 0, 002591 | 0, 001484 | 1, 746013 | 0, 222924 | -0, 00379 | 0, 008977 | -0, 00379 | 0, 008977 |
2. Анализ адекватности уравнения и значимости найденных коэффициентов уравнения. Отбраковка незначимых факторов.
В верхней части табл.2 приведены данные регрессионной статистики. Множественный R=0, 998893 и стандартная ошибка - 0, 002129, что свидетельствует о высокой степени совпадения вычисленных значений Х (по приведенному ниже уравнению регрессии) с экспериментальными значениями Х.
Оценка адекватности уравнения приведена в дисперсионном анализе. Высокая величина F = 180, 4229 и низкое значение Значимость F =0, 005521, что меньше уровня значимости 0, 05, указывают на адекватность уравнения регрессии.
В нижней части табл.2 выведены итоги расчета свободного коэффициента регрессии (Y-пересечение) и коэффициентов регрессии, стоящих перед аргументами Т, С, n, V и Р. Исходя из результатов расчетов уравнение регрессии выглядит следующим образом:
Х=-1, 40707 +0, 006185*Т-0, 00187*С-0, 04395*n+5, 81E-05*V+0, 002591*P (15)
Проверим значимость вычисленных коэффициентов регрессии. Значимость коэффициентов определяется по величине Р-значений, приведенных для каждого коэфициента в отдельном столбце. Коэффициенты уравнения значимы в том случае, если Р-значение меньше 0, 05 (уровня значимости). Из анализа величин Р-значений видно, что условию значимости отвечают коэффициенты Y-пересечение, и коэффициенты, стоящие перед аргументами Т и n. Исходя из этого, в уравнении регрессии могут быть отброшены другие аргументы: С, V и Р. То есть, степень превращения Х для приведенных экспериментальных данных зависит только от температуры Т и соотношения реагентов n.
3.Уточненные вычисления коэффициентов уравнения регрессии, вывод графиков подбора и остатков.
Для нахождения уточненного уравнения регрессии выполняют повторные вычисления, принимая в расчет в табл.1 исходных экспериментальных данных только значимые столбцы аргументов Т и n и функцию Х (столбцы №1, 3, 6).
Расчёты коэффициентов регрессии в программе Microsoft Excel выполняют аналогично вышеизложенным. Результаты расчетов приведены в табл.3, 4 и на рис.2, 3.
Таблица 3
Выводимые программой Microsoft Excel результаты уточненных расчетов коэффициентов регрессии, регрессионной статистики и дисперсионного анализа
| Регрессионная статистика | ||||||||
| Множественный R | 0, 995075 | |||||||
| R-квадрат | 0, 990174 | |||||||
| Нормированный R-квадрат | 0, 986243 | |||||||
| Стандартная ошибка | 0, 002837 | |||||||
| Наблюдения | ||||||||
| Дисперсионный анализ | ||||||||
| df | SS | MS | F | Значимость F | ||||
| Регрессия | 0, 004057 | 0, 002028 | 251, 9223 | 9, 57E-06 | ||||
| Остаток | 4, 03E-05 | 8, 05E-06 | ||||||
| Итого | 0, 004097 | |||||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95, 0% | Верхние 95, 0% | |
| Y-пересечение | -1, 07012 | 0, 108296 | -9, 8814 | 0, 000181 | -1, 3485 | -0, 79173 | -1, 3485 | -0, 79173 |
| Т | 0, 005486 | 0, 000293 | 18, 70805 | 8, 03E-06 | 0, 004732 | 0, 00624 | 0, 004732 | 0, 00624 |
| n | -0, 03039 | 0, 009116 | -3, 33332 | 0, 020704 | -0, 05382 | -0, 00695 | -0, 05382 | -0, 00695 |
Таблица 4
Величины расхождений расчетных и экспериментальных
значений (остатков) величины Х
| № наблюдения | Расчетная (предсказанная величина) X, доля | Остатки |
| 0, 819578 | 0, 000422 | |
| 0, 808014 | 0, 001986 | |
| 0, 871398 | -0, 0014 | |
| 0, 850046 | -4, 6E-05 | |
| 0, 862538 | -0, 00254 | |
| 0, 861946 | 0, 003054 | |
| 0, 818682 | -0, 00368 | |
| 0, 852797 | 0, 002203 |
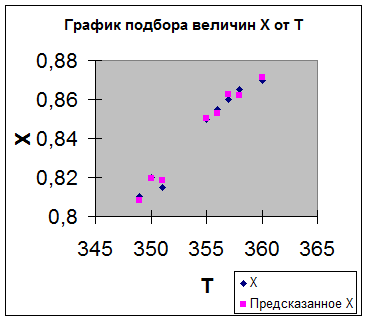 |
Рис.2
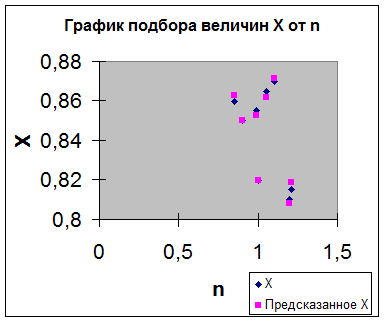 |
Рис.3
4. Анализ адекватности уточненного уравнения, значимости найденных коэффициентов уравнения, величин остатков и графиков подбора расчетных к экспериментальным значениям Х.
Анализ адекватности уравнения и значимости коэффициентов регрессии проводят аналогично вышеизложенному (см. табл.3). Значение множественного коэффициента R=0, 995075, близкое к 1, 0 и низкая величина стандартной ошибки - 0, 002837, свидетельствуют о высокой степени совпадения вычисленных значений Х (по приведенному ниже уравнению 16) с экспериментальными значениями Х. Уравнение (16) адекватно, поскольку значимость F составляет 9, 57E-06, что значительно меньше 0, 05.
Вычисленные коэффициенты, стоящие перед аргументами Т и n, значимы, так как величины Р-значений меньше 0, 05.
Таким образом, уточненное уравнение регрессии представляет собой:
Х=-1, 07012 +0, 005486*Т -0, 03039*n (16)
Следует отметить, что найденное уравнение регрессии (16) применимо только для диапазона изменения температуры Т=349..360оС и диапазона изменения соотношения реагентов n=0, 85..1, 21. При расширении диапазона аргументов оно может стать некорректным.
Величины расхождений расчетных и экспериментальных значений (остатков) Х приведены в табл.4. Из анализа данных табл.4 следует, что максимальная величина остатка не превышает 0, 003054, что показывает высокую степень совпадения расчетных и экспериментальных значений.
Графики подбора расчетных и экспериментальных значений Х по аргументам Т и n приведены на рис.2, 3. Приведенные на рис.2, 3 графики также подтверждают высокую степень совпадения расчетных и экспериментальных значений.
5. Оптимизация процесса по найденному уравнению регрессии
Найденное уравнение регрессии может быть использовано для оптимизации величины степени превращения Х. Целью оптимизации является нахождение величин Т и n, при которых достигается максимальная степень превращения.
Из анализа полученного линейного уравнения регрессии следует, что повышение температуры процесса и снижение соотношения реагентов до минимального значения приведет к увеличению степени превращения Х. Подставляя в уравнение (16) максимальное значение Т=360оС и минимальное значение n=0, 85, вычислим максимальное значение степени превращения:
Х= -1, 07012 +0, 005486*360 -0, 03039*0, 85= 0, 879
что является решением поставленной задачи.