
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Регрессионный анализ
|
|
Регрессионный анализ тесно связан с методами корреляционного и дисперсионного анализа. В отличие от дисперсионного анализа, с помощью которого исследуется зависимость количественного признака от одного или нескольких качественных признаков, и в отличие от корреляционно анализа, который изучает направление и силу статистической связи признаков, регрессионный анализ изучает вид зависимости признаков, т.е. параметры функции зависимости одного признака от другого или нескольких качественных признаков, в регрессионном анализе исследуется зависимость (количественного или качественного признака) от одного или нескольких количественных признаков. Прогноз в этом случае лучше поддается содержательной интерпретации, становится более ясным воздействие отдельных факторов, лучше понимается природа изучаемого явления.
Регрессии создают базу для расчетного экспериментирования с целью получения ответов на вопросы: «Что будет, если..?».
Регрессионный анализ предполагает решение двух задач:
1. Выбор независимой переменной, влияющей на зависимую величину, определение формы уравнения регрессии. Данная задача является путем анализа изучаемой взаимосвязи.
2. Оценивание параметров – решается с помощью того или иного статистического метода обработки данных наблюдения.
Регрессионный анализ – один из методов статистического моделирования. Моделью в данном случае является уравнение регрессии.
Методы регрессионного анализа можно классифицировать следующим образом:
1. По количеству независимых признаков: однофакторный, или простой (один независимый признак); многофакторный (два независимых признака и более).
2. По типу математической зависимости: линейный; нелинейный; логистический; экспоненциальная регрессия и т.д.
Однофакторная регрессионная модель является методом анализа двух признаков – независимого и зависимого.
Этапами построения регрессионной модели являются: анализ ассоциации зависимого признака с каждым из независимых путем оценки корреляции и построения двумерных графиков; отбор наиболее сильных ассоциаций; построение регрессионного уравнения.
Условия применения метода линейного регрессионного анализа:
· число объектов исследования должно быть в несколько раз больше числа прогностических (объясняющих) признаков);
· все анализируемые признаки должны быть количественными и нормально распределенными;
· независимые признаки могут быть количественными и/или качественными;
· взаимосвязи между каждым из данных независимого признака и зависимым признаком линейны в интервале изучаемых значений;
· каждое значение зависимого признака независимо от любого другого значения независимого признака;
· величина отклонений (вариаций) между фактически и прогнозируемым значением зависимой переменной, есть случайная величина с нормальным распределением и нулевым математическим ожиданием;
· все значения отклонений (вариации) между фактически и прогнозируемым значением зависимой переменной не коррелированны между собой и имеют одинаковую дисперсию.
Покажем, что для проведения регрессионного анализа может сделать средство Регрессия Пакета Анализа.
В отдельных таблицах оно вычисляет следующее:
- методом наименьших квадратов – коэффициенты линейной (относительно этих коэффициентов) функции регрессии; вид функции регрессии определяется структурой исходных данных; (Зам. Линейный регрессионный анализ заключается в подборе графика для набора наблюдений с помощью метода наименьших квадратов)
- коэффициент детерминации и связанные с ним величины (таблица регрессионная статистика); ·
- дисперсионную таблицу и критериальную статистику для проверки значимости регрессии (таблица Дисперсионный анализ); ·
- для каждого коэффициента регрессии – среднеквадратическое отклонение и другие его статистические характеристики, позволяющие проверить значимость этого коэффициента и построить для него доверительные интервалы; ·
- значения функции регрессии и остатки – разности между исходными значениями переменной Y и вычисленными значениями функции регрессии (таблица Ввод остатка); ·
- вероятности, соответствующие упорядоченным по возрастанию значениям переменной Y (таблица Вывод вероятности).
Кроме того, средство строит три типа графиков, которые будут показаны ниже.
Пусть входной интервал Х состоит из k диапазонов-столбцов, содержащих значения { xi 1}, { xi 2},..., { xik } переменных Х1, Х2,..., Х k. В каждом диапазоне содержится одинаковое количество значений. Входной интервал Y, состоящий из одного диапазона-столбца, должен содержать такое же количество значений. Средство вычисляет коэффициенты функции регрессии вида
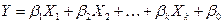
Диалоговое окно средства Регрессия показано на рис..
В поле Входной интервал Y вводится адрес диапазона, содержащего значения зависимой переменной Y. Диапазон должен состоять из одного столбца.
В поле входной интервал Х вводится адрес диапазона, содержащего значения переменной Х. Диапазон должен состоять из одного или нескольких столбцов, но не более чем из 16 столбцов.
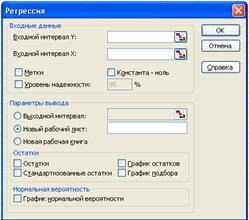
Если указанные в полях Входной интервал Y и Входной интервал Х диапазоны включают заголовки столбцов, то необходимо установить флажок опции Метки– эти заголовки будут использованы в выходных таблицах, сгенерированных средством Регрессия.
Флажок опции Константа - следует установить, если в уравнении регрессии константа b принудительно полагается равной нулю.
Опция Уровень надежности устанавливается тогда, когда необходимо построить доверительные интервалы для коэффициентов регрессии с доверительным уровнем, отличным от 0, 95, который используется по умолчанию. После установки флажка опции Уровень надежности становится доступным поле ввода, в котором вводится новое значение доверительного уровня.
В области Остатки имеются четыре опции: Остатки, Стандартизированные остатки, Графику остатков и график подбора. Если установлена хотя бы одна из них, то в выходных результатах появится таблица Вывод остатка, в которой будут выведены значения функции регрессии и остатки – разности между исходными значениями переменной Y и вычисленными значениями функции регрессии.
В области Нормальная вероятность имеется одна опция – График нормальной вероятности; ее установка порождает в выходных результатах таблицу Вывод вероятности и приводит к построению соответствующего графика.
В таблице Регрессионная статистика приводятся следующие данные
Множественный R – корень из коэффициента детерминации R 2, приведенного в следующей строке. Другое название этого показателя – индекс корреляции, или множественный коэффициент корреляции.
R–квадрат коэффициент дерминации R2; вычисляется как отношение регрессионной суммы квадратов к полной сумме квадратов. Величина 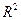 показывает, какая часть (доля) вариации объясняемой переменной обусловлена вариацией объясняющей переменной (
показывает, какая часть (доля) вариации объясняемой переменной обусловлена вариацией объясняющей переменной (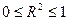 ). Чем ближе
). Чем ближе 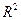 к единице, тем лучше регрессия аппроксимирует эмпирические данные. Если
к единице, тем лучше регрессия аппроксимирует эмпирические данные. Если 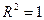 , то между
, то между 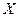 и
и 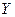 существует линейная функциональная зависимость. Если
существует линейная функциональная зависимость. Если 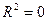 , то объясняемая переменная не зависит от данного набора объясняющих переменных.
, то объясняемая переменная не зависит от данного набора объясняющих переменных.
Имеющуюся расчетную величину R2расч необходимо сравнить с табличными (критическими) значениями R2крит для соответствующего уровня значимости (0, 05) (см. приложение 1). Если окажется, что R2расч> R2крит, то с упомянутой степенью вероятности (95%) можно утверждать, что анализируемая регрессия является значимой.
Нормированный R–квадрат скорректированный (адаптированный, поправленный(adjusted)) коэффициент детерминации.
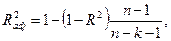
где 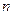 – число наблюдений,
– число наблюдений, 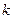 – число объясняющих переменных.
– число объясняющих переменных.
Недостатком коэффициента детерминации 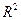 является то, что он увеличивается при добавлении новых объясняющих переменных, хотя это и не обязательно означает улучшение качества регрессионной модели. В этом смысле предпочтительнее использовать
является то, что он увеличивается при добавлении новых объясняющих переменных, хотя это и не обязательно означает улучшение качества регрессионной модели. В этом смысле предпочтительнее использовать 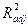 . В отличие от
. В отличие от 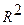 скорректированный коэффициент
скорректированный коэффициент 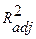 может уменьшаться при введении в модель новых объясняющих переменных, не оказывающих существенное влияние на зависимую переменную.
может уменьшаться при введении в модель новых объясняющих переменных, не оказывающих существенное влияние на зависимую переменную.
Стандартная ошибка регрессии 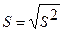 , где
, где 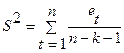 – необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии).
– необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии).
Наблюдения – количество значений переменной Y.
Дисперсионная таблица
В столбце SS приводятся суммы квадратов, в столбце df – число степеней свободы, в столбце MS –дисперсии. В столбце F вычислено значение критериальной статистики для проверки значимости регрессии. Это значение вычисляется как отношение регрессионной дисперсии к остаточной.
F и Значимость F позволяют проверить значимость уравнения регрессии, т.е. установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.
По эмпирическому значению статистики F проверяется гипотеза равенства нулю одновременно всех коэффициентов модели. Значимость F – теоретическая вероятность того, что при гипотезе равенства нулю одновременно всех коэффициентов модели F-статистика больше эмпирического значения F.
Уравнение регрессии значимо на уровне 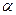 , если
, если 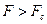 , где
, где 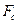 - табличное значение F -критерия Фишера (
- табличное значение F -критерия Фишера (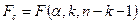 , см. приложение 2).
, см. приложение 2).
На уровне значимости 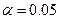 гипотеза
гипотеза 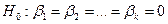 отвергается,
отвергается,
если Значимость 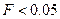 , и принимается, если Значимость
, и принимается, если Значимость 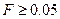 .
.
В следующей таблице, в столбце Коэффициенты, записаны вычисленные значения коэффициентов функции регрессии, при этом в строке Y - пересечение записано значение свободного члена 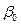 .
.
В столбце Стандартная ошибка вычислены среднеквадратические отклонения коэффициентов.
В столбце t-статистика записаны отношения значений коэффициентов к их среднеквадратическим отклонениям. Это значения критериальных статистик для проверки гипотез о значимости коэффициентов регрессии.
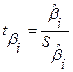 – t -статистика соответствующего коэффициента
– t -статистика соответствующего коэффициента 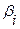 .
.
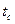 – критическая точка распределения Стьюдента,
– критическая точка распределения Стьюдента, 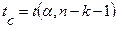 (см. приложение 3).
(см. приложение 3).
Если 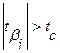 , то коэффициент
, то коэффициент 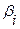 считается статистически значимым.
считается статистически значимым.
Если 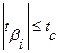 , то коэффициент
, то коэффициент 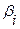 считается статистически незначимым. Это означает, что фактор
считается статистически незначимым. Это означает, что фактор 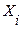 линейно не связан с зависимой переменной
линейно не связан с зависимой переменной 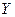 . Его наличие среди объясняющих переменных не оправдано со статистической точки зрения. Поэтому после установления того факта, что коэффициент
. Его наличие среди объясняющих переменных не оправдано со статистической точки зрения. Поэтому после установления того факта, что коэффициент 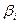 незначим, рекомендуется исключить из уравнения регрессии переменную
незначим, рекомендуется исключить из уравнения регрессии переменную 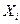 . Это не приведет к существенной потере качества модели, но сделает ее более корректной.
. Это не приведет к существенной потере качества модели, но сделает ее более корректной.
В столбце P-Значение вычисляются уровни значимости, соответствующие значениям критериальных статистик.
Если вычисленный уровень значимости меньше заданного уровня значимости (0, 05), то принимается гипотеза о значимом отличии коэффициента от нуля; в противном случае принимается гипотеза о незначимом отличии коэффициента от нуля.
P-Значение – вероятность, позволяющая определить значимость коэффициента регрессии 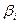 .
.
Для уровня значимости 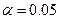 :
:
Если P-Значение 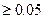 , то коэффициент
, то коэффициент 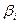 незначим, следовательно, гипотеза
незначим, следовательно, гипотеза 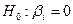 принимается.
принимается.
Если P-Значение 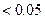 , то коэффициент
, то коэффициент 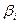 значим, следовательно, гипотеза
значим, следовательно, гипотеза 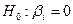 отвергается.
отвергается.
В столбцах 95% и 95% приводятся границы доверительных интервалов с доверительным уровнем 0, 95. Эти границы вычисляются по формулам
Нижние 95% = Коэффициент - Стандартная ошибка× 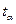
Верхние 95% = Коэффициент + Стандартная ошибка× 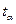
Здесь 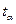 –квантиль порядка распределения Стьюдента с (n – k – 1) степенью свободы. В данном случае a = 0, 95. Аналогично вычисляются границы доверительных интервалов в столбцах 90, 0% и 90, 0%. Отметим, что если в диалоговом окне Регрессия не устанавливать опцию Уровень надежности, то будут повторены столбцы 95% и 95%.
–квантиль порядка распределения Стьюдента с (n – k – 1) степенью свободы. В данном случае a = 0, 95. Аналогично вычисляются границы доверительных интервалов в столбцах 90, 0% и 90, 0%. Отметим, что если в диалоговом окне Регрессия не устанавливать опцию Уровень надежности, то будут повторены столбцы 95% и 95%.
Рассмотрим таблицу Вывод остатка из выходных результатов средства.
Напомним, что эта таблица появляется в выходных результатах только тогда, когда установлена хотя бы одна опция в области Остатки диалогового окна Регрессия.
В столбце Наблюдение приводятся порядковые номера значений переменной Y.
В столбце Предсказанное Y вычисляются значения функции регрессии для тех значений переменной Х, которым соответствует порядковый номер i в столбце Наблюдение. В столбце Остатки содержатся разности (остатки) 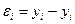 , а в столбце Стандартные остатки – нормированные остатки, которые вычисляются как отношения
, а в столбце Стандартные остатки – нормированные остатки, которые вычисляются как отношения 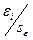 , где
, где 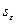 –среднеквадратическое отклонение остатков. Квадрат величины
–среднеквадратическое отклонение остатков. Квадрат величины 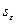 вычисляется по формуле
вычисляется по формуле 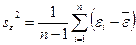 , где
, где 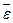 среднее остатков. Здесь величину
среднее остатков. Здесь величину 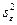 можно вычислить как отношение двух значений из дисперсионной таблицы: суммы квадратов остатков и степени свободы из строки Итого.
можно вычислить как отношение двух значений из дисперсионной таблицы: суммы квадратов остатков и степени свободы из строки Итого.
По значениям таблицы Вывод остатков средство Регрессия строит два типа графиков: графики остатков и графики подбора (если установлены соответствующие опции в области диалогового окна). Графики строятся для каждого компонента переменной Х в отдельности. На графиках остатков отображаются остатки, т.е. разности между
исходными значениями Y и вычисленными по функции регрессии для каждого значения компонента переменной Х. На графиках подбора отображаются как исходные значения Y, так и вычисленные значения функции регрессии для каждого значения компонента переменной Х.
Последней таблицей выходных результатов средства является таблица Вывод вероятности. Она появляется, если в диалоговом окне Регрессия установлена опция График нормальной вероятности. Значения в столбце Перцентиль вычисляются следующим образом. Вычисляется шаг 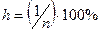 , первое значение равно h/2, последнее равно 100– h /2. Начиная со второго значения каждое последующее значение равно предыдущему, к которому прибавлен шаг h. В столбце Y приведены значения переменной Y, упорядоченные по возрастанию. По данным этой таблицы строится так называемый график нормального распределения. Он позволяет визуально оценить степень линейности зависимости между переменными Х и Y
, первое значение равно h/2, последнее равно 100– h /2. Начиная со второго значения каждое последующее значение равно предыдущему, к которому прибавлен шаг h. В столбце Y приведены значения переменной Y, упорядоченные по возрастанию. По данным этой таблицы строится так называемый график нормального распределения. Он позволяет визуально оценить степень линейности зависимости между переменными Х и Y