
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. Проведем графический анализ имеющихся данных, для этого построим диаграмму отражающую связь между признаками
|
|
Проведем графический анализ имеющихся данных, для этого построим диаграмму отражающую связь между признаками, представленными в таблице (рис.).
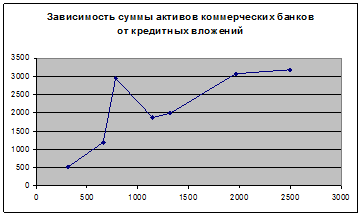
Анализ рисунка показывает наличие близкой к прямолинейной зависимости, так как точки расположены практически на прямой линии.
Построим линейную регрессионную модель с помощью встроенного средства в MS Excel Анализ данных.
Объясняемая переменная Y– Сумма активов
Объясняющая переменная X– Кредитные вложения
Надо найти оценки коэффициентов модели 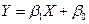
Для этого проделываем следующие действия:
1. Запишем исходные данные в виде таблицы Excel
2. Используя команду Сервис – Анализ данных, проведем регрессионный анализ имеющихся данных.
Проанализируем полученные данные.
1. Таблица Регрессионная статистика
| Регрессионная статистика | |
| Множественный R | 0, 787216748 |
| R-квадрат | 0, 619710208 |
| Нормированный R-квадрат | 0, 543652249 |
| Стандартная ошибка | 685, 9893982 |
| Наблюдения |
Так как полученный множественный коэффициент корреляции R=0, 78 и он больше 0, 7 то это говорит о наличии сильной линейной связи между переменными Х и Y.
Коэффициент детерминации R-квадрат равен 0, 61 что составляет 61%. Этот результат можно истолковать так: исследуемый воздействующий фактор объем кредитных вложений объясняет 61% вариации анализируемой функции, остальные 39% остаются не объясненными и могут быть связано с влиянием других, неучтенных факторов.
Сравним расчетную величину R2расч =0, 61(это то, что нам выдал Excel) с табличными (критическими) значениями R2крит , который для соответствующего уровня значимости (0, 05) равен 0, 569. Имеем, что R2расч> R2крит, следовательно с упомянутой степенью вероятности (95%) можно утверждать, что анализируемая регрессии является значимой.
Стандартная ошибка показывает, что фактическая величина суммы активов отличается от прогнозируемых показателей не более чем на 685, 98 млр. руб. под воздействием величины кредитных вложений.
2. Таблица Дисперсионный анализ
| Дисперсионный анализ | |||||
| df | SS | MS | F | Значимость F | |
| Регрессия | 3834235, 59 | 8, 147868 | 0, 035637501 | ||
| Остаток | 2352907, 27 | 470581, 5 | |||
| Итого | 6187142, 86 |
Число степеней свободы df, суммы квадратов SS, дисперсии MS используются для вычисления критериальной статистики F, и Значимости F.
Итак, по полученным данным оценим значимость уравнения регрессии.
Уравнение регрессии значимо на уровне 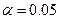 , если
, если 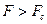 , где
, где 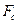 - табличное значение F -критерия Фишера (
- табличное значение F -критерия Фишера (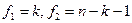 ). Для нашей модели
). Для нашей модели 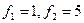 и по таблице фишера
и по таблице фишера 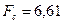 .
.
Поскольку 8, 14> 6, 61, то с вероятностью 95 % можно утверждать, что рассматриваемое уравнение адекватно (его коэффициенты отличны от нуля) и способно с указанной достоверностью предсказывать экспериментальные результаты.
Вероятность вычисленного значения критериальной статистики составила 0, 03 (столбец F-значение). Так как полученная вероятность меньше заданного уровня значимости, равного 0, 05, то мы принимаем гипотезу о том, что все коэффициенты регрессии не равны нулю.
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95, 0% | Верхние 95, 0% | |
| Y-пересечение | 816, 29 | 521, 59 | 1, 57 | 0, 18 | -524, 49 | 2157, 07 | -524, 49 | 2157, 07 |
| Кредитные вложения, млрд руб | 1, 04 | 0, 37 | 2, 85 | 0, 04 | 0, 10 | 1, 98 | 0, 10 | 1, 98 |
По данным первого столбца получаем вид уравнения регрессии 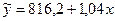 .
.
Стандартные ошибки коэффициентов во втором столбце указывают на отклонение фактических коэффициентов от прогнозируемых.
t-статистика третьего столбца говорит о статистической значимости коэффициентов регрессии:
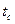 – критическая точка распределения Стьюдента,
– критическая точка распределения Стьюдента, 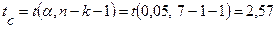 .
.
Так как 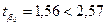 , то коэффициент
, то коэффициент 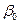 является статистически не значимым и его можно исключить из модели уравнения.
является статистически не значимым и его можно исключить из модели уравнения.
Р-значение третьего столбца позволяет определить значимость коэффициентов регрессии.
Так как Р-значение коэффициента 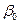 : 0, 18 и оно больше 0, 05, то коэффициент
: 0, 18 и оно больше 0, 05, то коэффициент 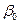 незначим и следовательно равен нулю.
незначим и следовательно равен нулю.
Так как Р-значение коэффициента 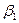 : 0, 04 и оно меньше 0, 05, то коэффициент
: 0, 04 и оно меньше 0, 05, то коэффициент 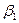 значим и, следовательно, неравен нулю.
значим и, следовательно, неравен нулю.
В последних столбцах рассматриваемой таблицы указаны доверительные интервалы попадания коэффициентов регрессии.
3. таблица вывод остатка
| ВЫВОД ОСТАТКА | |||
| Наблюдение | Предсказанное Сумма активов, млрд руб. | Остатки | Стандартные остатки |
| 1140, 628 | -622, 6281 | -0, 99426 | |
| 1502, 515 | -308, 515 | -0, 49266 | |
| 1632, 878 | 1308, 1223 | 2, 088919 | |
| 2007, 279 | -142, 2794 | -0, 2272 | |
| 2191, 873 | -194, 873 | -0, 31119 | |
| 2862, 459 | 203, 54126 | 0, 325032 | |
| 3419, 368 | -243, 3682 | -0, 38863 |
Во втором столбце представлены значения функции регрессии, вычисленные от имеющихся значений переменной Х.
В столбце остатки представлена разница между фактическими значениями переменой Y и вычисленными значениями в первом столбце последней таблицы.
Стандартные остатки в последнем столбце говорят о наличии выбросов в первоначальном наборе данных, если стандартный остаток больше 2 и меньше -2. из таблицы видно, что выбросом является 3 значение таблицы.
4. таблица Вывод вероятности
| ВЫВОД ВЕРОЯТНОСТИ | ||
| Персентиль | Сумма активов, млрд руб. | |
| 7, 14285714 | ||
| 21, 4285714 | ||
| 35, 7142857 | ||
| 64, 2857143 | ||
| 78, 5714286 | ||
| 92, 8571429 |
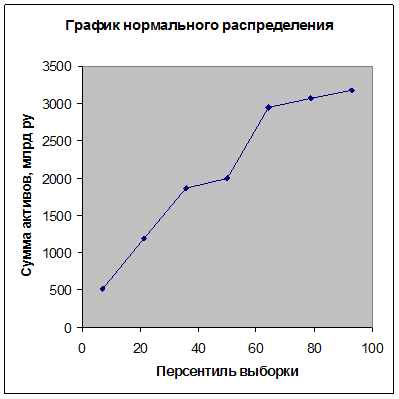
По данным этой таблицы строится график нормального распределения для визуальной оценки степени линейности между переменными Х и Y.
Задачи:
1. Определить направление и тесноту связи, предварительно у становив характер связи между четырьмя факторам по 15 банкам:
| № Банка | Суммарный актив, млрд долл. | Объем вложений акционеров, млрд долл. | Чистый доход, млрд долл. | Депозиты млрд долл. |
| 507, 2 | 19, 5 | 352, 9 | 448, 1 | |
| 506, 6 | 19, 8 | 187, 1 | 451, 9 | |
| 487, 8 | 21, 1 | 375, 2 | 447, 9 | |
| 496, 0 | 18, 6 | 287, 9 | 444, 3 | |
| 493, 6 | 19, 6 | 44, 0 | 443, 2 | |
| 458, 9 | 11, 7 | 462, 4 | 411, 7 | |
| 429, 3 | 10, 5 | 459, 5 | 328, 6 | |
| 386, 9 | 13, 6 | 511, 3 | 314, 7 | |
| 311, 5 | 10, 8 | 328, 6 | 259, 4 | |
| 302, 2 | 10, 9 | 350, 0 | 187, 7 | |
| 262, 0 | 10, 3 | 298, 7 | 238, 5 | |
| 242, 4 | 10, 6 | 529, 3 | 269, 4 | |
| 231, 9 | 8, 5 | 320, 0 | 284, 0 | |
| 214, 3 | 6, 7 | 502, 0 | 172, 3 | |
| 208, 4 | 8, 3 | 194, 9 | 166, 4 |
Провести регрессионный анализ, возможных связей между факторами.
2. По данным о сумме активов (y), кредитных вложений (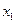 ) и величине собственного капитала (
) и величине собственного капитала (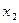 ) коммерческих банков построить множественное уравнение связи. Связь предполагается линейной. Провести анализ полученной модели.
) коммерческих банков построить множественное уравнение связи. Связь предполагается линейной. Провести анализ полученной модели.
| Банк | Сумма активов млрд руб. | Кредитные вложение, млрд руб. | Собственный капитал, млрд руб |
| y | x1 | x2 | |