
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Применение инструмента Регрессия (Анализ данных в EXCEL).
|
|
Для проведения регрессионного анализа выполните следующие действия:
1. Выберите команду СервисÞ Анализ данных.
2. В диалоговом окне Анализ данных выберите инструмент Регрессия, а затем щелкните на кнопке ОК
3. В диалоговом окне Регрессия в поле Входной интервал Y введите адрес одного диапазона ячеек, который представляет зависимую переменную. В поле Входной интервал Х введите адреса одного или нескольких диапазонов, которые содержат значения независимых переменных (Рисунок 4.1.).
4. Если выделены и заголовки столбцов, то установить флажок Метки в первой строке.
5. Выберите параметры вывода. В данном примере Новая рабочая книга
6. В поле Остатки поставьте необходимые флажки.
7. ОК.
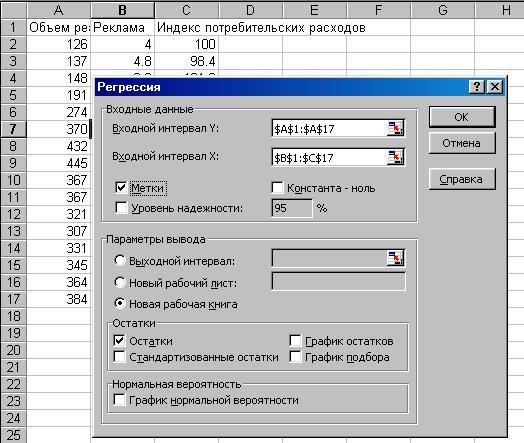
Рисунок 4.1. Диалоговое окно Регрессия подготовлено к выполнению анализа данных.
Результат регрессионного анализа содержится в таблицах 4.4 –4.7. Рассмотрим содержание этих таблиц.
Таблица 4.4.
| Регрессионная статистика | |
| Множественный R | 0.927 |
| R-квадрат | 0.859 |
| Нормированный R-квадрат | 0.837 |
| Стандартная ошибка | 41.473 |
| Наблюдения | 16.000 |
Таблица 4.5
| Дисперсионный анализ | ||||
| df | SS | MS | F | |
| Регрессия | 136358.334 | 68179.167 | 39.639 | |
| Остаток | 22360.104 | 1720.008 | ||
| Итого | 158718.438 |
Таблица 4.6
| Коэффициенты | Стандартная ошибка | t-статистика | |
| Y-пересечение | -1471.314 | 259.766 | -5.664 |
| Реклама | 9.568 | 2.266 | 4.223 |
| Индекс потребительских расходов | 15.753 | 2.467 | 6.386 |
Таблица 4.7
| ВЫВОД ОСТАТКА | ||
| Наблюдение | Предсказанное | Остатки |
| 142, 25 | -16, 25 | |
| 124, 70 | 12, 30 | |
| 159, 24 | -11, 24 | |
| 242, 35 | -51, 35 | |
| 247, 02 | 26, 98 | |
| 307, 06 | 62, 94 | |
| 361, 20 | 70, 80 | |
| 416, 80 | 28, 20 | |
| 424, 18 | -57, 18 | |
| 350, 32 | 16, 68 | |
| 345, 37 | -24, 37 | |
| 334, 72 | -27, 72 | |
| 386, 79 | -55, 79 | |
| 352, 05 | -7, 05 | |
| 353, 23 | 10, 77 | |
| 361, 73 | 22, 27 |
Пояснения к таблице 4.4.
| Регрессионная статистика | |||
| № | Наименование в отчете EXCEL | Принятые наименования | Формула |
| Множественный R | Коэффициент множественной корреляции, индекс корреляции | 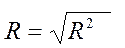
| |
| R-квадрат | Коэффициент детерминации, R2 | 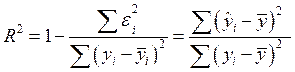
| |
| Нормированный R-квадрат | Скорректированный R2 | 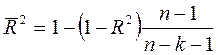
| |
| Стандартная ошибка | Стандартная ошибка оценки | 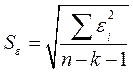
| |
| Наблюдения | Количество наблюдений, n | n |
Пояснения к таблице 4.5.
| Df – число степеней свободы | SS – сумма квадратов | MS | F – критерий Фишера | |
| Регрессия | k =2 | 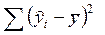
| 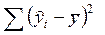 /k /k
| 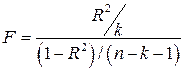
|
| Остаток | n-k-1 = 13 | 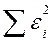
| 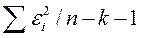
| |
| Итого | n-1 = 15 | 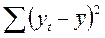
|
Пояснения к таблице 4.6.
Во втором столбце таблицы 4.6. содержатся коэффициенты уравнения регрессии a0, a1, a2. В третьем столбце содержатся стандартные ошибки коэффициентов уравнения регрессии, а в четвертом - t-статистика, используемая для проверки значимости коэффициентов уравнения регрессии.
Уравнение регрессии зависимости объема реализации от затрат на рекламу и индекса потребительских расходов можно записать в следующем виде:
y = -1471.314 + 9.568х1 + 15.754х2
3.Оценка качества всего уравнения регрессии
В таблице 4.7 приведены вычисленные (предсказанные) по модели значения зависимой переменной Y и значения остаточной компоненты  .
.
Значение коэффициентов детерминации и множественной корреляции можно найти в таблице Регрессионная статистика.
Коэффициент детерминации:
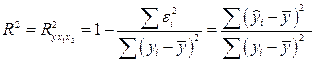
= 1- 22360.104/158718.44 = 136358.3/158718.44 = 0.859
Он показывает долю вариации результативного признака под воздействием изучаемых факторов. Следовательно, около 86% вариации зависимой переменной учтено в модели и обусловлено влиянием включенных факторов.
Коэффициент множественной корреляции R:
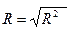 = 0.927.
= 0.927.
Он показывает тесноту связи зависимой переменной Y с двумя включенными в модель объясняющими факторами.
4. Проверку значимости уравнения регрессии произведем на основе вычисления F-критерия Фишера:
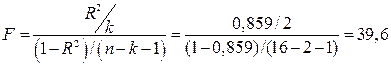
Значение F-критерия Фишера можно найти в таблице 4.6 протокола EXCEL.
Табличное значение F-критерия при доверительной вероятности 0, 95 при 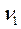 = k =2 и
= k =2 и 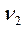 =n – k -1= 16 – 2 - 1=13 составляет 3.81. Табличное значение F-критерия можно найти с помощью функции FРАСПОБР (Рис. 4.3)
=n – k -1= 16 – 2 - 1=13 составляет 3.81. Табличное значение F-критерия можно найти с помощью функции FРАСПОБР (Рис. 4.3)
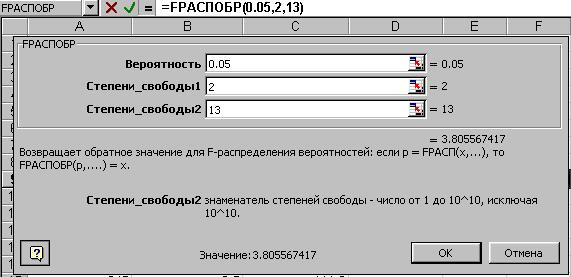
Рисунок 4.3. Определение табличного значения F-критерия.
Поскольку F 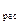 > F
> F 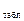 , уравнение регрессии следует признать адекватным.
, уравнение регрессии следует признать адекватным.
4.Оценить с помощью t - критерия Стъюдента статистическую значимость коэффициентов уравнения множественной регрессии.
Значимость коэффициентов уравнения регрессии a0, а 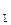 , а
, а 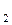 оценим с использованием t-критерия Стьюдента.
оценим с использованием t-критерия Стьюдента.
Значения t-критерия вычислим по формулам:
taj=aj/Saj
Saj = 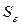 ´
´ 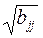 ,
,
где bjj - диагональный элемент матрицы (ХТ Х)-1.
(Xт X)-1 = 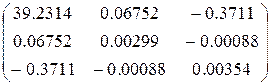
b11 =39.2314
b22 = 0.00299
b33 = 0.00354
ta0 = -1471.314 /259.766 = -1471.314 / 41.473 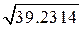 =- 5.664
=- 5.664
ta1 = 9.5684/2.2659 = 9.5684 / 41.473 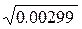 = 4.223
= 4.223
ta2 = 15.7529/2.4669 = 15.7529/ 41.473 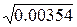 = 6.3858
= 6.3858
Расчетные значения t-критерия Стьюдента для коэффициентов уравнения регрессии а 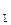 , а
, а 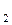 приведены в четвертом столбце таблицы 4.7 протокола EXCEL. Табличное значение t-критерия Стьюдента можно найти с помощью функции СТЬЮДРАСПОБР (Рис. 4.4)
приведены в четвертом столбце таблицы 4.7 протокола EXCEL. Табличное значение t-критерия Стьюдента можно найти с помощью функции СТЬЮДРАСПОБР (Рис. 4.4)

Рисунок 4.4. Определение табличного значения t-критерия Стьюдента.
Табличное значение t-критерия при 5% уровне значимости и степенях свободы (16-2-1=13) составляет 2, 16. Так как |t 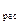 |> t
|> t 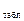 , то коэффициенты a1, а
, то коэффициенты a1, а 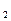 и существенны (значимы).
и существенны (значимы).
.
Рисунок 4.2. График остатков.