
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Величины
|
|
Рассмотрим дискретную случайную величину Х с конечным набором ее возможных значений х 1, х 2, …, х n. В результате некоторого испытания случайная величина Х примет одно из этих значений. Иначе говоря, произойдет одно из следующих несовместных событий, образующих полную группу: Х = х 1, Х = х 2, …, Х = х n.
Обозначим вероятности этих событий через р 1= Р (Х = х 1), р 2= Р (Х = х 2), …, р n= Р (Х = х n). Рассматриваемые события образуют полную группу, поэтому сумма вероятностей этих событий или, иначе, сумма вероятностей появления возможных значений случайной величины равна единице, т.е.
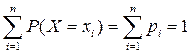
Таким образом, каждому возможному значению случайной величины х к поставлено в соответствие число р к – вероятность появления этого значения, т.е. получена зависимость между возможными значениями случайной величины и вероятностями появления этих значений. Эта зависимость определяет основные формы закона распределения дискретной случайной величины. Она может быть представлена таблично, графически и аналитически.
Простейшее представление такой зависимости в виде таблицы называется рядом распределения.
Рядом распределения вероятностей дискретной случайной величины называется ее закон распределения, записанный в виде таблицы, в первой строке которой приведены все возможные значения случайной величины (обычно в порядке возрастания), а во второй строке – соответствующие этим значениям вероятности.
Ряд распределения для дискретной случайной величины с конечным множеством значений имеет вид:
| Х | х 1 | х 2 | … | х n |
| Р | р 1 | р 2 | … | р n |
Для значений второй строки данной таблицы сумма всех вероятностей равна 1. Таким образом, само название этой таблицы говорит о том, что единица как бы распределена между всеми значениями случайной величины согласно имеющимся вероятностям.
Ряд распределения является табличной формой задания закона распределения. Однако он может быть задан, как и функция в математическом анализе, графическим способом. Если по оси абсцисс отложить возможные значения случайной величины, а по оси ординат – вероятности этих значений, то, соединив точки (х к, р к) последовательно отрезками прямой линии, получим ломаную, которая является графической формой закона распределения дискретной случайной величины и называется многоугольником распределения вероятностей.
Иногда многоугольником распределения вероятностей называют, по аналогии с геометрическими фигурами, саму фигуру (многоугольник), расположенную под ломаной линией.
Пример 1. В денежной лотерее разыгрывается 10 выигрышей в 50 рублей и 20 выигрышей по 10 рублей при общем числе билетов 100. Найти закон распределения в виде ряда распределения и многоугольника распределения выигрыша Х для владельца одного лотерейного билета.
Решение. Возможные значения для случайной величины Х это 0 рублей, 10 рублей и 50 рублей. Вероятности этих значений могут быть найдены по классической формуле, т.е.
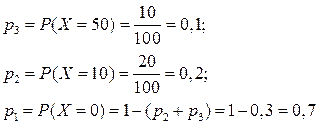
Таким образом, ряд распределения имеет вид:
| Х | |||
| Р | 0, 7 | 0, 2 | 0, 1 |
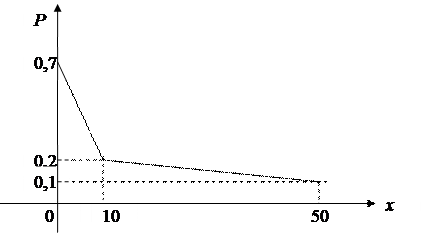 Построим многоугольник распределения:
Построим многоугольник распределения: