Биномиальный закон распределения

Пусть производится n независимых испытаний, в каждом из которых может появиться или не появиться событие А. Вероятность появления этого события в каждом единичном испытании постоянна, не зависит от номера испытания и равна р = Р (А). Отсюда вероятность не появления события А в каждом испытании также постоянна и равна q =1– р.

Рассмотрим случайную величину Х равную числу появлений события А в n испытаниях. Очевидно, что значения этой величины равны

х ₁=0 – событие А в n испытаниях не появилось;

х ₂=1 – событие А в n испытаниях появилось один раз;

х ₃=2 – событие А в n испытаниях появилось два раза;

…………………………………………………………..

х_{n +1} = n – событие А в n испытаниях появилось все n раз.

Вероятности этих значений могут быть вычислены по формуле Бернулли:

,

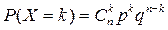где к =0, 1, 2, …, n.

Биномиальным законом распределения называется распределение дискретной случайной величины Х, равной числу успехов в n испытаниях Бернулли, с вероятностью успеха р.

Итак, дискретная случайная величина имеет биномиальное распределение (или распределена по биномиальному закону), если ее возможные значения 0, 1, 2, …, n, а соответствующие вероятности вычисляются по формуле Бернулли.

Биномиальное распределение зависит от двух параметров р и n.

Ряд распределения случайной величины, распределенной по биномиальному закону, имеет вид:

Х			…	k	…	n
Р			…		…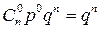

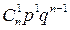
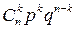
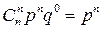
Пример 2. Производится три независимых выстрела по мишени. Вероятность попадания при каждом выстреле равна 0, 4. Случайная величина Х – число попаданий в мишень. Построить ее ряд распределения.

Решение. Возможными значениями случайной величины Х являются х ₁=0; х ₂=1; х ₃=2; х ₄=3. Найдем соответствующие вероятности, используя формулу Бернулли. Нетрудно показать, что применение этой формулы здесь вполне оправдано. Отметим, что вероятность не попадания в цель при одном выстреле будет равна 1-0, 4=0, 6. Получим

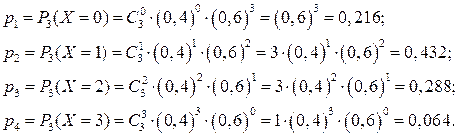
Ряд распределения имеет следующий вид:

Нетрудно проверить, что сумма всех вероятностей равна 1. Сама случайная величина Х распределена по биномиальному закону. ■

Заключение

Итак, на лекции было рассмотрено понятие случайного события. На конкретных примерах были представлены различные виды этих событий. Были показаны основные арифметические операции, которые можно производить над случайными событиями, и введено понятие вероятности случайного события. Также было рассмотрено понятие случайной величины, определены дискретная и непрерывная случайные величины. Затем было рассмотрено понятие закона распределения случайной величины и формы этого закона для дискретной случайной величины.

Задание: выучить определения случайного события и его различных видов: достоверного, невозможного, элементарного, составного; определения совместных и несовместных в данном испытании событий, полной группы событий, пространства элементарных событий; определения суммы и произведения событий, вероятности случайного события. Все определения дополнять соответствующими примерами. Выучить определения случайной величины, дискретной и непрерывной случайных величин, закона распределения случайной величины; разобраться с формами и видами законов распределения дискретной случайной величины.

Литература

Основная:

1. Большакова Л.В. Теория вероятностей для экономистов – М.: Финансы и статистика, 2009.

2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2000.

3. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 1999.

Дополнительная:

4. Кремер Н.Ш. Теория вероятностей и математическая статистика. – М.: ЮНИТИ-ДАНА, 2003.

5. Ниворожкина Л.И., Морозова З.А., Герасимова И.А., Житников И.В. Основы статистики с элементами теории вероятностей для экономистов: Руководство для решения задач. – Ростов н/Д: Феникс, 1999.