
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Случайные погрешности (e).
|
|
Погрешности, причиной которых являются случайные, неконтролируемые изменения условий измерения, называются случайными погрешностями. Так как на условия измерения действует множество различных факторов, причины возникновения случайных погрешностей не всегда известны и часто непредсказуемы. Действие этих факторов приводит к тому, что отклонение результата измерения от истинного значения концентрации носит статистический, вероятностный характер.
При параллельных измерениях величина случайных погрешностей изменяется случайным образом. Какова будет погрешность каждого единичного измерения предсказать нельзя. Но можно оценить наиболее вероятную максимальную случайную погрешность методики анализа.
Часто методику анализа называют – «Методика выполнения измерений, МВИ»).
Мерой случайной погрешности методики анализа является стандартное отклонение генеральной совокупности - s (сигма).
Под генеральной совокупностью понимают бесконечно большое число измерений. Это понятие идеализированное (воображаемое, недостижимое практически).
На практике при выполнении анализа по стандартизованной методике получают ограниченное число результатов. Совокупность ограниченного числа результатов измерений называют выборкой, а их количество - объемом выборки. Мерой случайной погрешности в этом случае является стандартное отклонение небольшого объема выборки S, которое часто называют среднеквадратичным отклонением (СКО)
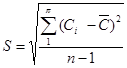

S - стандартное отклонение малой выборки (СКО)
Сi - результат единичного (и-того) измерения концентрации.
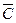 - среднее значение концентрации из n результатов измерений
- среднее значение концентрации из n результатов измерений
n - количество параллельных измерений концентрации,
(n-1) - принято называть числом степеней свободы (В справочниках обозначается " f ")
Пример.
При определении концентрации хрома в стальном образце атомно-эмиссионным методом анализа выполнили четыре параллельных измерения и получили данные (Cr %): 1, 44; 1, 45; 1, 43; 1, 45. Рассчитаем стандартно отклонение малой выборки по формуле 4.5
| №п/п | Сi | 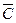
| 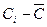
| (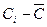 )2 )2
|
| 1, 44 | -0, 002 | 0, 04·10-4 | ||
| 1, 45 | 0, 008 | 0, 64 10-4 | ||
| 1, 43 | 1, 442 | -0, 012 | 1, 44 10-4 | |
| 1, 45 | 0, 008 | 0, 64 10-4 | ||
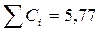
| 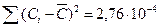
|
а) 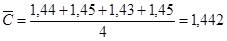 б)
б) 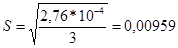
Если объем выборки достаточно велик - (не менее 30), то стандартное отклонение выборки " S" (среднее квадратичное отклонение) можно принять равным s.
При объеме выборки более 30 среднее квадратичное отклонение «S» характеризует случайную погрешность методики анализа и является наилучшей оценкой стандартного отклонения генеральной совокупности s.
Иногда для оценки случайной погрешности используют величину, равную квадрату стандартного отклонения, называемую дисперсией выборки S2