Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Кривая распределения случайных погрешностей.
|
|
Как уже говорилось, случайные погрешности вызываются случайными причинами, действия которых неодинаково при параллельных измерениях. Случайная погрешность различна, даже в тех случаях, когда параллельные измерения производятся одним и тем же аналитиком, в один день, с одними и теми же реактивами, посудой, приборами.
Например, взвешивая одну и ту же навеску несколько раз на одних весах, с одними и теми же гирями можно получить заметно отличающиеся результаты. Причиной случайных погрешностей может оказаться колебания воздуха, неодинаково влияющее на чашки весов или нагревание одной чашки весов от приближения руки.
Абсолютные случайные погрешности изменяются от одного параллельного измерения к другому. Они могут быть и положительными и отрицательными, могут оказаться и очень маленькими и достаточно большими.
График, отражающий зависимость количества измерений с данной случайной погрешностью от величины этой погрешности, называется кривой распределения случайных погрешностей.
Случайные погрешности химического анализа обычно подчиняются нормальному (Гауссовому) закону распределения. (рис. 1)
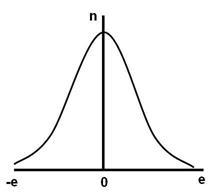
Рисунок 1. Кривая нормального распределения случайных погрешностей «e» построенная по большому числу (n > 30) параллельных измерений. (Кривая Гаусса)
Нормальному распределению случайных погрешностей соответствует симметричная кривая. Для нормального распределения характерно:
· Одинаковые по абсолютной величине, но противоположные по знаку погрешности встречаются одинаково часто.
· Большая часть измерений концентрируется вблизи нулевой погрешности, т.е. эти измерения близки к истинному значению измеряемой величины, если отсутствует систематическая погрешность.
· Число измерений с большой погрешностью тем меньше, чем больше сама погрешность
Зная величину σ, можно с некоторой уверенностью определить возможный интервал случайных погрешностей единичного измерения. Эта уверенность называется - доверительной вероятностью и обозначается буквой «Р». Чем с большей доверительной вероятностью (уверенностью) мы хотим представить результат анализа, тем большим оказывается диапазон случайных погрешностей.
Например, (смотри рис. 2)можно с 95%-ной доверительной вероятностью (уверенностью) P считать, что случайная погрешность любого единичного измерения не превышает 2σ, а с доверительной вероятностью 99, 7% - она не более 3σ и только при 68% доверительной вероятности, погрешность каждого измерения не больше σ.
Рисунок 2 Границы интервалов случайных погрешностей при различной доверительной вероятности.
Иногда величину случайной погрешности оценивают относительным стандартным отклонением.
Относительное стандартное отклонение RSD - отношение стандартного отклонения к средней концентрации выборки.
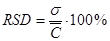(при аттестации методики анализа)
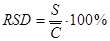(для малого объема выборки)
Пример. При определении хлороформа в воде методом газовой хроматографии произвели пять измерения концентрации, получили результаты мг/л: 0, 043; 0, 046; 0, 044; 0, 043; 0, 045. Нужно определить относительное стандартное отклонение – RSD малой выборки.
| 
| 
|
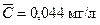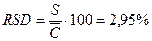