
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Способы управления исполнительными асинхронными микродвигателями
|
|
Способы регулирования угловой скорости ротора исполнительного асинхронного микродвигателя, или способы управления, вытекают из теории о форме вращающегося магнитного поля. Изменяя напряжение управления Uу и углы β и γ раздельно или одновременно, воздействуют на форму магнитного поля статора и тем самым на угловую скорость ротора.
Амплитудное управление (рис. 2.9). Обмотку возбуждения В подключают к сети переменного тока с номинальным напряжением U1. Ha обмотку управления У подают сигнал – напряжение управления Uy, сдвинутое по фазе относительно напряжения возбуждения U1 на угол 90°. Управление угловой скоростью ротора осуществляют изменением амплитуды напряжения управления при неизменной его фазе.
При равенстве приведенных напряжений управления и возбуждения (Uy'=U1) эффективный коэффициент сигнала
α е = kтрα = 1, (2.11)
а поле статора в двигателе круговое (α = Uy/U1 – коэффициент сигнала при амплитудном управлении).
С изменением напряжения управления эффективный коэффициент сигнала становится отличным от единицы, а поле – эллиптическим. При α е = 0, т. е. снятом сигнале управления, поле статора становится пульсирующим.
Фазовое управление (рис. 2.10). Обмотку возбуждения В подключают к сети переменного тока с номинальным напряжением U1. Ha обмотку управления У подают номинальное напряжение, переменное по фазе относительно напряжения возбуждения. Номинальным называют такое напряжение управления, которое соответствует равенству UУ' = U1. Управление угловой скоростью ротора осуществляют изменением фазы напряжения управления (угла β). За коэффициент сигнала принимают sin β. При sin β = 1 вращающееся магнитное поле статора круговое; при l > sin β > 0 – эллиптическое, при sin β = 0 – пульсирующее.
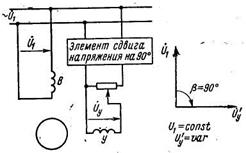
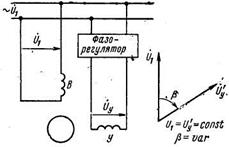
Рис. 2.9 Рис. 2.10
Пространственное управление (рис. 2.11). Обмотку возбуждения В подключают к сети переменного тока с номинальным напряжением U1 На обмотку управления У подают номинальное напряжение, сдвинутое по фазе относительно напряжения возбуждения на 90°. Управление угловой скоростью ротора производят изменением пространственного угла γ сдвига обмоток возбуждения В и управления У. За коэффициент сигнала принимают sin γ. При sin γ = l вращающееся магнитное поле статора круговое; при 1 > sin γ > 0 – эллиптическое, при sin γ = 0 – пульсирующее.
Амплитудно-фазовое управление с конденсатором в цепи возбуждения (конденсаторное) (рис. 2.12, а). Обмотку управления У подключают к сети переменного тока через регулятор напряжения; напряжение управления Uy совпадает по фазе с напряжением сети U1. Сдвиг фаз тока, а следовательно, и напряжения на обмотке возбуждения по отношению к обмотке управления осуществляется конденсатором, который включают последовательно с обмоткой возбуждения. Управление двигателем происходит за счет изменения амплитуды напряжения управления.
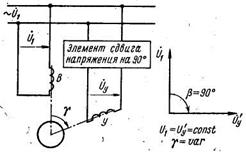
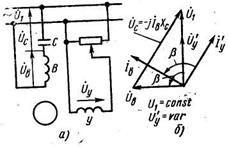
Рис. 2.11 Рис. 2.12
Несмотря на то что фаза напряжения управления не изменяется (совпадает с фазой напряжения сети), при изменении напряжения управления наблюдается одновременное изменение как значения, так и фазы напряжения возбуждения Uв. Такое же явление происходит и при изменении угловой скорости ротора за счет изменения момента нагрузки при неизменном напряжении управления. Это объясняется тем, что напряжение возбуждения Uв равно геометрической разности напряжений в сети U1 и на конденсаторе UC (рис. 2.12, б):
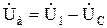 . (2.12)
. (2.12)
Напряжение на конденсаторе Uc при изменении напряжения управления или угловой скорости ротора меняется вследствие изменения тока в цепи возбуждения, который является функцией скольжения и коэффициента сигнала [см. значения симметричных составляющих Iв в (2.5)]:
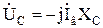 . (2.13)
. (2.13)
Следовательно, меняется по амплитуде и фазе напряжение на обмотке возбуждения Uв.
Поскольку круговое поле существует в двигателе только при соблюдении условия Uв = jU'y, при заданном значении емкости конденсатора в цепи возбуждения круговое поле возможно только при строго определенных коэффициенте сигнала α 0 = Uу0/U1 и значении скольжения s.
В случае создания кругового поля при пуске двигателя (s = l) коэффициент сигнала α 0 и емкостное сопротивление конденсатора ХС0 определяют по формулам, получаемым при анализе симметричных составляющих токов:
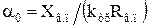 ; (2.14)
; (2.14)
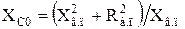 , (2.15)
, (2.15)
где Xв.п, Rв.п – индуктивное и активное сопротивления схемы замещения фазы В (см. рис. 2.8) при пуске (s = 1).
При иных напряжениях управления и режимах работы поле двигателя уже не будет круговым. Пуск двигателя в условиях кругового поля обеспечивает заданный пусковой момент при минимальной потребляемой мощности.
Увеличение в определенных пределах емкости С по отношению к C0 позволяет увеличивать пусковой момент. Максимальное значение пускового момента достигается при ХC = ХC M в условиях эллиптического поля и возросшей потребляемой мощности, что необходимо учитывать при анализе теплового режима двигателя.
Емкостное сопротивление ХC M при α = α 0 и s = 1 определяют по формуле
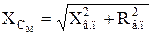 . (2.16)
. (2.16)
Сравнивая выражение для ХC 0 и ХC M, нетрудно заметить, что ХC M < ХC 0, т.е. СМ > С0. Максимальный пусковой момент больше пускового момента при круговом поле в n раз;
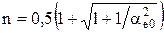 ,
,
где α e0 = α 0kтр – эффективный коэффициент сигнала при круговом поле.
В соответствии с изложенным различают два основных вида пуска асинхронных микродвигателей: при круговом поле и при максимальном пусковом моменте.
При заданном пусковом моменте Mп = Mп0 использование при пуске емкости См позволяет уменьшить сигнал управления в n раз. Общая потребляемая мощность возрастает при этом в (n4+1)/(2n2) раз.
Рассмотренные способы управления обеспечивают весьма широкий диапазон регулирования угловой скорости ротора, определяемый отношением минимальной и максимальной угловых скоростей. У исполнительных микродвигателей с полым немагнитным ротором он достигает 1/100 – 1/200.
Механические и регулировочные характеристики исполнительных асинхронных микродвигателей в относительных единицах (ω 2∂ = ω 2/ω 1 = l - s; М∂ = М/Мп0) соответственно представлены на рис. 2.13 и 2.14 для наиболее распространенных в схемах автоматики амплитудного (а), фазового (б) и амплитудно-фазового (в) способов управления.
Рис. 2.13
Рис. 2.14
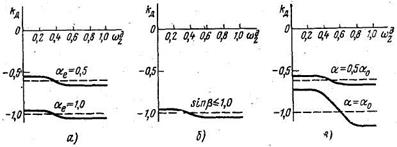
Рис. 2.15
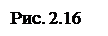
 Анализ механических характеристик по уравнению момента (2.9) показывает, что при всех способах управления характеристики нелинейны и их жесткость уменьшается с уменьшением сигнала управления. Нелинейность механической характеристики, т. е. отклонение ее от линейной, определяется как отношение наибольшей по абсолютному значению разности между действительным вращающим моментом и значением момента, рассчитанным по уравнению прямой линии, проходящей через точки холостого хода и пускового момента, к значению пускового момента, т. е. ∆ М∂ max/Мп∂ (рис. 2.13, а). Улучшению линейности механических характеристик способствуют увеличение активного сопротивления ротора и в меньшей степени уменьшение индуктивного сопротивления рассеяния обмоток статора и ротора. Однако, как известно, увеличение активного сопротивления ротора ухудшает энергетические показатели двигателя. Поэтому у исполнительных асинхронных микродвигателей, работающих в системах автоматики, допускается нелинейность порядка 10%. На рис. 2.15, а–в показаны зависимости коэффициента внутреннего демпфирования от угловой скорости и коэффициента сигнала при различных способах управления.
Анализ механических характеристик по уравнению момента (2.9) показывает, что при всех способах управления характеристики нелинейны и их жесткость уменьшается с уменьшением сигнала управления. Нелинейность механической характеристики, т. е. отклонение ее от линейной, определяется как отношение наибольшей по абсолютному значению разности между действительным вращающим моментом и значением момента, рассчитанным по уравнению прямой линии, проходящей через точки холостого хода и пускового момента, к значению пускового момента, т. е. ∆ М∂ max/Мп∂ (рис. 2.13, а). Улучшению линейности механических характеристик способствуют увеличение активного сопротивления ротора и в меньшей степени уменьшение индуктивного сопротивления рассеяния обмоток статора и ротора. Однако, как известно, увеличение активного сопротивления ротора ухудшает энергетические показатели двигателя. Поэтому у исполнительных асинхронных микродвигателей, работающих в системах автоматики, допускается нелинейность порядка 10%. На рис. 2.15, а–в показаны зависимости коэффициента внутреннего демпфирования от угловой скорости и коэффициента сигнала при различных способах управления.
Как видно из рис. 2.13 и 2.15, наиболее линейными являются характеристики при фазовом управлении, причем жесткость характеристик практически не меняется при изменении коэффициента сигнала. Наименее линейны механические характеристики при амплитудно-фазовом управлении. При всех способах управления механические характеристики обеспечивают устойчивость работы во всем диапазоне двигательного режима и с уменьшением, коэффициента сигнала смещаются в сторону меньших моментов и угловых скоростей. Вращающий момент и механическая мощность, развиваемые двигателем, получаются наибольшими при амплитудно-фазовом управлении. Это объясняется тем, что при увеличении угловой скорости ротора конденсаторного микродвигателя несколько увеличиваются напряжение, магнитный поток обмотки возбуждения и соответственно вращающий момент двигателя по сравнению с моментом при амплитудном и фазовом управлениях. Недостатком амплитудно-фазового управления является некоторое снижение устойчивости в области малых угловых скоростей.
Анализ регулировочных характеристик (см. рис. 2.14) и зависимостей коэффициента передачи от коэффициента сигнала (рис. 2.16) показывает, что при всех способах управления они нелинейны. Нелинейность, т. е. отклонение действительной регулировочной характеристики от линейной, наибольшая в режиме холостого хода и зависит в основном от тех же параметров двигателя, что и нелинейность механических характеристик. Ближе всех к линейным характеристики микродвигателя с фазовым управлением, затем следуют характеристики микродвигателей с амплитудным и амплитудно-фазовым управлениями (рис. 2.16). При амплитудно-фазовом управлении (конденсаторном) нелинейность можно изменять в определенном диапазоне путем выбора соответствующей емкости конденсатора, т.е. воздействуя на эллиптичность магнитного поля. Линейность регулировочных характеристик улучшается при усилении эллиптичности поля. Поэтому наибольшую линейность и крутизну характеристики имеют в начальной части. Для обеспечения линейности регулирования двигатель должен работать при малых сигналах и относительных угловых скоростях. Уменьшение относительных угловых скоростей наиболее эффективно достигается повышением рабочей частоты напряжения питания двигателя, так как при этом пропорционально повышается синхронная угловая скорость.
Количественно нелинейность регулировочной характеристики ∆ ω дв определяется как отношение наибольшей по абсолютному значению разности между угловой скоростью, рассчитанной по уравнению прямой линии, аппроксимирующей действительную регулировочную характеристику в номинальном диапазоне напряжений управления, и действительной угловой скоростью к наибольшему значению угловой скорости в номинальном диапазоне напряжения управления. Пример определения нелинейности при холостом ходе показан на рис. 2.14, а, где ∆ ω дв = ∆ ω ∂ 2max/ω ∂ 20. При нелинейности механических характеристик меньше 10% нелинейность регулировочной характеристики холостого хода не превышает 20% в диапазоне изменения коэффициента сигнала 0 – 0, 7.
Пусковой момент при всех способах управления прямо пропорционален сигналу управления и в относительных единицах равен эффективному коэффициенту сигнала.
Мощностью возбуждения является мощность, потребляемая цепью обмотки возбуждения микродвигателя:
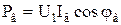 , (2.17)
, (2.17)
где φ в – угол сдвига между напряжением сети и током в обмотке возбуждения.
Мощность управления – это мощность, потребляемая обмоткой управления микродвигателя:
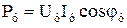 , (2.18)
, (2.18)
где φ у – угол сдвига между напряжением и током в обмотке управления.
Анализ выражения (2.18) показывает, что при амплитудном управлении мощность управления исполнительных асинхронных микродвигателей примерно такая же, как и при амплитудно-фазовом, и так же сильно зависит от коэффициента сигнала. При фазовом управлении эта мощность с уменьшением коэффициента сигнала практически не меняется (рис. 2.17). В этом отношении амплитудный и амплитудно-фазовый способы управления имеют существенное преимущество перед фазовым.
Коэффициент полезного действия исполнительных асинхронных микродвигателей несколько ниже, чем у одинаковых по мощности асинхронных микродвигателей общего применения, из-за повышенного активного сопротивления ротора, причем наиболее высокий к.п.д. имеют двигатели с амплитудным управлением, затем следуют двигатели с амплитудно-фазовым управлением (конденсаторные). Самый низкий к.п.д. у двигателей с фазовым управлением (за счет большой мощности управления). Более высокий коэффициент мощности имеют микродвигатели с амплитудно-фазовым управлением благодаря наличию конденсатора в цепи возбуждения (cos φ = 0, 8 ÷ 0, 95).
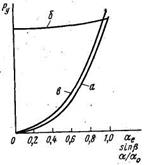
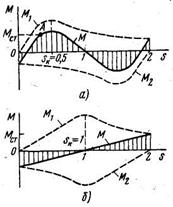
Рис. 2.17 Рис. 2.18
Среди схем питания исполнительных асинхронных микродвигателей наибольшей простотой отличается схема конденсаторного микродвигателя, так как она не имеет сложных устройств для сдвига фаз между напряжениями управления и возбуждения.
Таким образом, амплитудно-фазовый способ управления с конденсатором в цепи возбуждения двигателя имеет ряд преимуществ, поэтому его широко применяют в схемах автоматики и вычислительных устройствах. Однако в каждом конкретном случае выбор способа управления должен определяться условиями работы системы, звеном которой является двигатель, и требованиями, предъявляемыми к этому звену.
У исполнительных асинхронных микродвигателей, работающих в системах автоматики, важно обеспечить отсутствие самохода.
Рассмотрим явление самохода асинхронного микродвигателя. Для этого воспользуемся зависимостями M = f(s) момента прямой M1 и обратной M2 последовательностей при пульсирующем поле статора и различных значениях критического скольжения sк (рис. 2.18).
На рис. 2.18 кривую результирующего момента M при пульсирующем поле статора получают как сумму моментов прямой и обратной последовательностей.
В случае, показанном на рис. 2.18, а, критическое скольжение по отношению к полю прямой последовательности sк = 0, 5 и результирующий момент в пределах двигательного режима (s = 0 ÷ 1) имеет одно направление с моментом прямой последовательности, а значит, и с направлением вращения ротора. Следовательно, ротор не остановится после снятия сигнала управления, если момент сопротивления Mст будет меньше максимального результирующего момента (момента самохода). Возникает параметрический самоход, и двигатель работает с угловой скоростью и моментом, соответствующими точке А характеристики M = f(s).
В случае, показанном на рис. 2.18, б, критическое скольжение по отношению к полю прямой последовательности sк = 1. Здесь кривая результирующего момента пересекает ось скольжения только в одной точке s = 1, и в пределах двигательного режима момент M отрицателен, т. е. является тормозящим, направленным против вращения ротора. Поэтому при снятии сигнала управления ротор обязательно остановится. То же самое произойдет и при sк > l.
Следует отметить, что значение sк (при соблюдении условия sк > l), при котором гарантируется отсутствие параметрического самохода, зависит от схемы включения обмотки управления. Например, при снятии сигнала управления размыканием цепи обмотки управления требуемое критическое скольжение больше, чем при снятии сигнала без размыкания.
У асинхронных микродвигателей возможен также технологический самоход, который вызывается образованием короткозамкнутых витков в магнитопроводе и обмотке. При этом двигатель начинает работать как двигатель с экранированными полюсами.
Реверсирование исполнительных асинхронных микродвигателей производят изменением фазы напряжения управления на 180° (например, путем переключения концов обмотки У). При этом магнитное поле статора начинает вращаться в противоположную сторону и изменяется направление вращения ротора.
ЛЕКЦИЯ №8