Основы регрессионного анализа

Тема 2. Двумерная регрессионная модель

План:

1. Основы регрессионного анализа

2. Линейная регрессия. Двумерная модель

Основы регрессионного анализа

Регрессионный анализ есть статистический метод исследования зависимости случайной величины Y от переменных 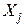(j =1, 2,...k), рассматриваемых в регрессионном анализе как k неслучайных величин, независимо от истинного закона распределения .

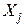Обычно предполагается, что случайная величина Y имеет нормальный закон распределения с условным математическим ожиданием 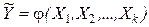, являющимся функцией от аргументов 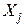, и постоянной, не зависящей от аргументов дисперсией 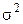. Пусть из генеральной совокупности 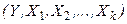берется выборка объемом n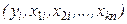 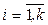. Требуется по выборке найти оценку уравнений регрессии 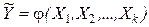и исследовать его свойства.

Переменная Y называется зависимой, а x₁, x₂, …, x_k – объясняющими переменными. Возникают следующие вопросы:

1) зависит ли Y от x₁, x₂, …, x_k, и, если зависит, то от каких из них,

2) какова наиболее адекватная форма зависимости,

3) можно ли, используя полученную зависимость, прогнозировать и предсказывать значения y при заданных значениях x₁, x₂, …, x_k.

Регрессионный анализ предлагает строить искомую зависимость в форме

y = f(x₁, x₂, …, x_k) + e, (1)

где f(x₁, x₂, …, x_k) – некоторая заданная функция, коэффициенты которой, вообще говоря, неизвестны. Величина e включает в себя факторы, неизвестные исследователю, или случайные составляющие, которые задают погрешность приближенной формулы y» f(x₁, x₂, …, x_k). Зависимость вида (1) называется регрессионной моделью.

Среди регрессионных моделей выделяют следующие:

А) модели, линейные по переменным и по параметрам, то есть модели вида

y = b₀ + b₁ x₁ + b₂ x₂ + … + b_k x_k + e,

Б) модели, не линейные по переменным, но линейные по параметрам, то есть модели вида

y = b₀ + b₁ x₁ + b₂ x₁² + b₃ x₁ x₂ + b₄ x₂² + b₅ / x₂ +… + e,

В) модели, не линейные по переменным и по параметрам, то есть модели вида

y = b₀ + b₁ x₁ + b₂ x₂² + b₃ x₁^A + b₄ x₂^C + exp(b₅ x₃) +sin(b₆ x₁ x₂ )… + e.

Модель вида А) называется множественной линейной регрессией.

Модель вида Б) относится к нелинейным регрессионным моделям.

Модели вида А) и Б) в основном и применяются для решения задач эконометрики. Модель вида В) в некоторых случаях может быть сведена к А) или Б) за счет преобразования переменных. Однако в общем случае работа с моделью вида В) возможна только при использовании специальных компьютерных программ.

Все перечисленные модели содержат набор коэффициентов, которые являются параметрами моделей. Для нахождения этих параметров используется метод наименьших квадратов (МНК). Сущность этого метода состоит в следующем. Пусть вид функции f(x₁, x₂, …, x_k) известен с точностью до входящих в нее коэффициентов b = { b_k }. Запишем f = f(b, u), где u = (x₁, x₂, …, x_k). Рассмотрим набор данных по переменным y и u:

y₁, y₂, …, y_n; u₁, u₂, …, u_n. (2)

Составим функцию L = L(b) как сумму квадратов отклонений фактических значений y_i от теоретических значений f(b, u_i), то есть

L(b) = S(y_i - f(b, u_i))².

Оценки коэффициентов b находятся как решение задачи на экстремум

L(b) ® min. (3)

При выполнении определенных предположений относительно величины e решение задачи (3) дает нужные нам оценки коэффициентов b^*, входящих в изучаемую зависимость.

Полагаем, что случайная составляющая e удовлетворяет условиям (основные предположения МНК):

1) M e = 0, D e = s² = const > 0,

2) пары величин e_i = y_i - b₀ - b u_i, e_j = y_j - b₀ - b u_j являются не коррелированными при всех i, j = 1, …, n, i ¹ j,

3) величин e_i имеют нормальное распределение, i = 1, …, n.

Важным этапом по выбору регрессионной модели является графический анализ данных. Наиболее удобно изучать зависимости между двумя переменными, а именно y и x_j. Построив на плоскости «облако точек» в форме пар (y_i, x_ji), можно подобрать одну из формул, связывающих y и x_j, либо заметить, что зависимости может и не быть.