Линейная регрессия. Двумерная модель

Необходимо найти оценку двумерного линейного уравнения регрессии:

.

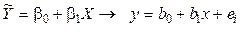Для оценки неизвестных параметров 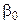и 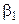из двумерной генеральной совокупности 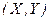берется выборка объемом 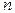, где 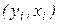- результат i-того наблюдения (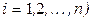. Оценку 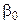и 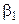производится с помощью метода наименьших квадратов (МНК).

Согласно МНК, в качестве оценок неизвестных параметров 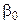и 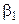следует брать такие значения выборочных характеристик 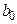и 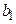, которые минимизируют сумму квадратов отклонений:

.

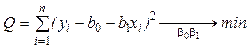Исследуя функцию 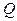на минимум, получим:

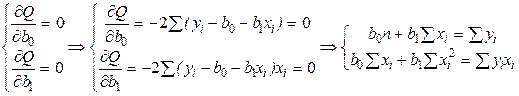
Решая эту систему уравнений, например, методом Крамера получаем:

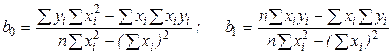
Оценка 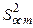остаточной дисперсии 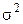имеет вид:

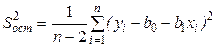
Проверка значимости и нахождение интервальных оценок коэффициентов регрессии

1. Для проверки значимости уравнения регрессии, т.е. гипотезы 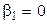, используют критерий, основанный на статистике:

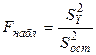, где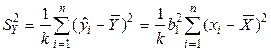

Нулевая гипотеза отвергается, если .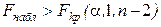

2. Интервальные оценки:

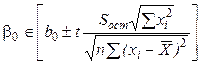, (6.6) ,

,

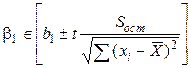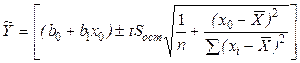где t - определяется по таблице Стьюдента: 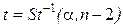, 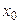- заданное значение Х, для которого находится интервальная оценка параметра .

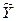Доверительную с надежностью 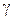оценку для интервала предсказания в точке 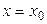определяют из условия:

.

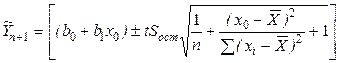Контрольные вопросы:

1. Модель простой регрессии: описание модели простой линейной регрессии. Основные характеристики модели.

2. Метод наименьших квадратов (МНК). Теорема Гаусса – Маркова.

3. Проверка соответствия двумерной регрессионной модели выборочным данным с помощью коэффициента детерминации.

4. Проверка соответствия двумерной регрессионной модели выборочным данным с помощью теста Фишера.

5. Статистические свойства МНК-оценок параметров двумерной регрессии.

6. Проверка значимости коэффициентов двумерной регрессии с помощью
t-теста. Доверительные интервалы для коэффициентов регрессии. Прогнозирование. Проверка соответствия построенной модели новым данным.

Литература:

1. Магнус Я.Р., Катышев П.К., Пересецкий А.А.. Эконометрика. Начальный курс. – М.: Дело, 1997.

2. Доугерти К. Введение в эконометрику. М.: ИНФРА-М, 1997.

3. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. Учебник для вузов. – М.: ЮНИТИ, 1998.

4. Эконометрика. Учебное пособие /И.И. Елисеева. С.В. Курышева, Д.М. Гордиенко и др. – М.: Финансы и статистика, 2001.

5. Геращенко И.П. Эконометрика. Практикум. Электронный учебник. – ИПП., 2004.

6. Замков О.О. Эконометрические методы в макроэкономическом анализе (курс лекций). – М. Диалог МГУ, 1999.

7. Сайт «Прикладная эконометрика» МГУ https://crow.academy.ru/econometrics/.

8. Колемаев В.А., Староверов О.В., Турундаевский В.Б.. Теория вероятностей и математическая статистика. – М.: Высш. шк., 1991.

9. Теория статистики. \\ под ред. Р.А.Шмойловой. – М: Финансы и статистика. – 2002.