Линейная регрессия. Множественная модель

Рассмотрим общий случай линейной регрессии, когда условное математическое ожидание 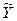есть функция k переменных:

.

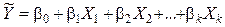В матричном виде это уравнение примет вид: 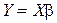, где 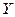- вектор-столбец наблюдений размерности 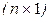; 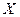- матрица факторных признаков размерности 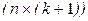; 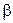- вектор неизвестных параметров размерности .

; ; .

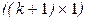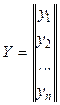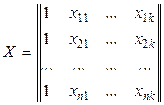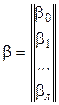Оценка МНК вектора 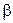имеет вид:

,

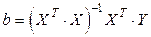где 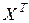- транспонированная матрица Х, 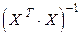- матрица, обратная матрице .

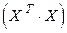Несмещенная оценка остаточной дисперсии:

,

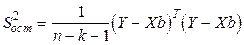Оценка ковариационной матрицы вектора 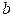определяется из выражения:

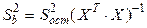
По диагонали в этой матрице стоят дисперсии компонент этого вектора: .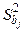

Проверка значимости и доверительные интервалы.

1. Выдвигаем гипотезу:

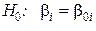(если проверяем значимость 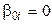). Находим статистический критерий:

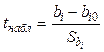
Гипотеза отвергается при .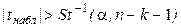

2. Критерий проверки совместной гипотезы - критерий Хотеллинга:

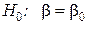(если проверяем значимость 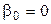). Находим статистический критерий:

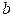- матрица-столбец выборочных коэффициентов регрессии, 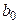- матрица - столбец возможных значений ( 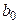- нулевая матрица, если проверяется значимость). Чтобы опровергнуть гипотезу необходимо, чтобы

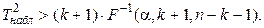
4. Значимость уравнения регрессии, т.е. гипотеза 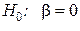, проверяется с помощью критерия, основанного на статистике:

,

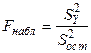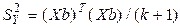- сумма квадратов отклонений, обусловленных регрессией. Уравнение значимо, если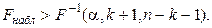

5. Доверительный интервал для параметров уравнения регрессии:

,

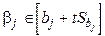где .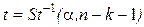

6. Интервальная оценка для условного математического ожидания Y, определяемого в точке 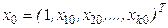начальных условий, равна

,

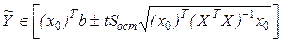Доверительная оценка для интервала предсказания 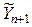определяется как

.

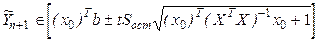7. Проверка гипотезы о равенстве отдельного прогноза. Выдвинем гипотезу: 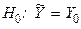. Статистический критерий для проверки этой гипотезы имеет вид:

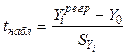
Гипотеза отвергается при .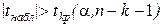

Для совместной гипотезы - критерий Хотеллинга:

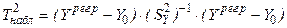
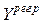- матрица-столбец значений Y, найденных по уравнению регрессии, - матрица - столбец возможных значений Y, 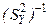- обратная матрицу к матрице 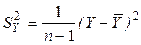, где Y - матрица (6.11). Гипотеза отвергается, если

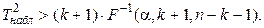
8. Проверка гипотезы о равенстве коэффициентов различных уравнений регрессии. Пусть мы имеем р уравнений регрессии. Выдвигаем гипотезу 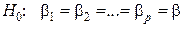, где 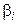- матрица коэффициентов регрессии i - того уравнения, 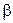- матрица общего уравнения регрессии, построенного по 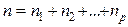наблюдениям. Отношение 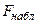определяется в виде:

,

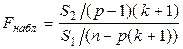где 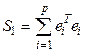, 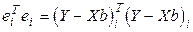- сумма квадратов выборочных ошибок i - того уравнения регрессии; , где 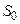- сумма квадратов выборочных ошибок общего уравнения регрессии. Гипотеза принимается, если .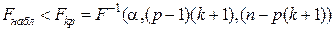