
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Распространение выборочных результатов
⇐ ПредыдущаяСтр 2 из 2
|
|
Таблица 1 - Среднее значение показателя в выборочной совокупности
| № | Показатель | Повторный отбор | Бесповторный отбор | Малая выборка |
| 1) | Средняя ошибка выборки | 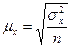 (1) (1)
| 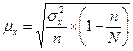 (2) (2)
|  (3*) (3*)
|
где 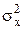 - дисперсия выборки;
n - количество единиц в выборочной совокупности.
N - объем генеральной совокупности. - дисперсия выборки;
n - количество единиц в выборочной совокупности.
N - объем генеральной совокупности.
| *малая выборка объемом менее 20 единиц | |||
| Формулу (1) можно использовать и при бесповторном отборе, если объем выборки не превышает 5% от объема генеральной совокупности. | ||||
| 2) | Предельная ошибка | 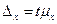 (4)
где t - коэффициент доверия, определяемый по таблицам функции Лапласа.
Предельная ошибка применяется тогда, когда хотят получить результат с вероятностью, большей чем 0, 683. (4)
где t - коэффициент доверия, определяемый по таблицам функции Лапласа.
Предельная ошибка применяется тогда, когда хотят получить результат с вероятностью, большей чем 0, 683.
| ||
| 3) | Границы среднего значения признака в генеральной совокупности | 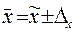 (5)
где (5)
где 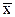 - средняя в генеральной совокупности; - средняя в генеральной совокупности;
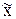 - выборочная средняя. - выборочная средняя.
| ||
| 4) | Пределы генеральной средней |
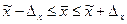 (6) (6)
| ||
| 5) | Оптимальная численность выборки | 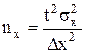 (7) (7)
| 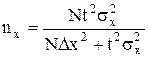 (8) (8)
| - |
Таблица 2 - Среднее значение доли альтернативного признака в выборочной совокупности
| № | Показатель | Повторный отбор | Бесповторный отбор | Малая выборка |
| 1) | Средняя ошибка доли альтернативного признака выборки | 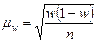 (9) (9)
|  (10) (10)
| 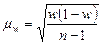 (11) (11)
|
| где μ w - средняя ошибка доли альтернативного признака; w - доля альтернативного признака в выборочной совокупности; n - количество единиц в выборочной совокупности; N - количество единиц в генеральной совокупности. | малая выборка объемом менее 20 единиц | |||
| Формулу (9) можно использовать и при бесповторном отборе, если объем выборки не более 5% от объема генеральной совокупности. | ||||
| 2) | Предельная ошибка доли альтернативного признака | 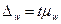 (12)
где t - коэффициент доверия, определяемый по таблицам функции Лапласа.
Предельная ошибка применяется тогда, когда хотят получить результат с вероятностью, большей чем 0, 683. (12)
где t - коэффициент доверия, определяемый по таблицам функции Лапласа.
Предельная ошибка применяется тогда, когда хотят получить результат с вероятностью, большей чем 0, 683.
| ||
| 3) | Границы доли альтернативного признака в генеральной совокупности | 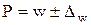 (13) (13)
| ||
| 4) | Пределы доли альтернативного признака в генеральной совокупности |  (14)
где Р - доля альтернативного признака в генеральной совокупности;
w - выборочная доля альтернативного признака;
Δ w - предельная ошибка доли альтернативного признака. (14)
где Р - доля альтернативного признака в генеральной совокупности;
w - выборочная доля альтернативного признака;
Δ w - предельная ошибка доли альтернативного признака.
| ||
| 5) | Оптимальная численность выборки |  (15) (15)
| 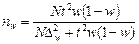 (16) (16)
| - |