Второе доказательство

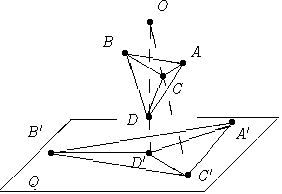
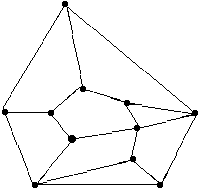
Второе доказательство. Пусть X - выпуклый многогранник и F - какая-либо его грань. Возьмем точку O, лежащую вне многогранника вблизи его грани F. Спроектируем многогранник с помощью центральной проекции из точки O на какую-нибудь плоскость Q, параллельную плоскости грани F. Тогда эта грань спроектируется на некоторый выпуклый многоугольник M, лежащий в Q, а проекции всех остальных граней многогранника X являются выпуклыми многоугольниками, которые образуют разбиение многоугольника M. На рис. 3 многогранник X есть тетраэдр ABCD, его проекция - треугольник A'B'C'. В случае многранника общего вида проекция изображена на рис. 4.

При проектировании каждая вершина многогранника X переходит в вершину разбиения многоугольника M; при этом числа вершин у X и у разбиения M совпадают. Аналогично, числа ребер у X и у разбиения M одинаковы. С другой стороны, разбиение многоугольника M имеет на одну грань меньше, чем многогранник X. Сейчас мы понимаем под B, P и Г соответственно число вершин, ребер и граней разбиения M. Мы докажем, что

B - P + Г = 1.

откуда следует формула Эйлера (1).

Рис. 3	Рис. 4

Итак, мы имеем дело с плоским выпуклым многоугольником M, разбитым на грани. Пусть Г ₃ - число трехугольных,..., Г_m - число m -угольных граней. Таким образом, m есть число сторон (или углов) той грани, у которой это число наибольшее. Если многоугольник (или грань) имеет n сторон, то, как известно, сумма его внутренних углов равна p(n - 2). Поэтому сумма всех внутренних углов всех граней равна

S = p[ Г ₃ + 2 Г ₄ +... + (m - 2) Г_m ]. (4)

Мы хотим теперь преобразовать это выражение. Пусть P ₁ - число ребер разбиения, лежащих на границе многоугольника M, и P ₂ - число внутренних ребер. Тогда P = P ₁ + P ₂. Так как каждое внутреннее ребро относится к двум граням, а каждое граничное - к одной, то, суммируя ребра по всем граням, получаем

3 Г ₃ + 4 Г ₄ +... + mГ_m = P ₁ + 2 P ₂. (5)

Используя очевидное равенство Г = Г ₃ + Г ₄ +... + Г_m и равенство (5), мы можем преобразовать правую часть (4) так

Г ₃ + 2 Г ₄ +... + (m - 2) Г_m = (3 Г ₃ + 4 Г ₄ +... + mГ_m) - 2(Г ₃ + Г ₄ +... + Г_m) =

= (3 Г ₃ + 4 Г ₄ +... + mГ_mГ_m) - 2 Г = P ₁ + 2 P ₂ - 2 Г. (6)

Вычислим теперь сумму углов S другим способом. Пусть B ₁ - число вершин разбиения, лежащих на границе многоугольника M, и B ₂ - число внутренних вершин разбиения. Сумма всех внутренних углов самого многоугольника M (а не всех его граней!) равна p(B ₁ - 2), а сумма всех углов граней вокруг каждой внутренней вершины равна 2p. Поэтому

S = p(B ₁ - 2) + 2p B ₂. (7)

Из равенства (4), (6) и (7) получаем

P ₁ + 2 P ₂ - 2 Г = B ₁ - 2 + 2 B ₂

или

2(P ₂ - P ₂ + Г) = B ₁ - 2 + 2 B ₂.

Но так как B ₁ = P ₁, B = B ₁ + B ₂ и P = P ₁+ P ₂, то

B - P + Г = (B ₁ + B ₂) - (P ₁ + P ₂) + Г = 1,

что и требовалось.

Переходим к выводу следствий из формулы Эйлера. Всюду в дальнейшем под многогранником мы понимаем выпуклый многогранник. Назовем степенью вершины многогранника число выходящих из нее ребер. Ясно, что степень каждой вершины не меньше трех. Обозначим через B ₃ число вершин степени 3, через B ₄ - число вершин степени 4 и т. д. Тогда

B = B ₃ + B ₄ +... B_m, (8)

Здесь m - максимальная степень вершины и B ₁ = B ₂ = 0. Для нас будет безразлично, каково точное значение числа m; поэтому формулу (8) мы запишем в таком виде

B = B ₃ + B ₄ + B ₅ +.... (8')

Каждая грань многогранника есть выпуклый многоугольник, число сторон (или углов) которого равно 3 или 4 и т.д. Обозначим через Г_i число i -угольных граней многогранника (i = 3, 4,...). Тогда

Г = Г ₃ + Г ₄ + Г ₅ +.... (9)

Суммируя ребра по всем вершинам и учитывая, что каждое ребро соединяет две вершины и поэтому учитывается дважды, получаем

2 P = 3 B ₃ + 4 B ₄ + 5 B ₅ +.... (10)

Аналогично, сумммируя ребра по всем граням и учитывая, что каждое ребро принадлежит двум граням и поэтому считается дважды, имеем

2 P = 3 Г ₃ + 4 Г ₄ + 5 Г ₅ +.... (11)

Обратите внимание на то, что во все соотношения (8)-(11), как и в формулу Эйлера (1), пара чисел B и Г (а также пары чисел B ₃ и Г ₃, B ₄ и Г ₄ и т. д.) входят симметрично, т. е. эти соотношения остаются справедливыми, если заменить в них число B числом Г, число B ₃ числом Г ₃ и т. д., и наоборот. Поэтому любому утверждению, например, о гранях многогранника, выведенному из формулы (1) и равенств (8)-(11), соответствует аналогичное (двойственное) утверждение о его вершинах. В этом состоит так называемый принцип двойственности. В частности, двойственными друг другу являются равенства (10) и (11). Формула Эйлера двойственна сама себе. Этот принцип используется ниже.

Чтобы получить первое следствие из формулы (1), умножим обе ее части на 2, затем подставим в нее вместо B, 2 P и Г их значения из (8), (10) и (9). Тогда получим

2(B ₃ + B ₄ +...) - (3 B ₃ + 4 B ₄ +...) + 2(Г ₃ + Г ₄ +...) = 4. (12)

Двойственным образом получаем

2(B ₃ + B ₄ +...) - (3 Г ₃ + 4 Г ₄ +...) + 2(Г ₃ + Г ₄ +...) = 4. (13)

Теперь складываем равенства (12) и (13), затем переносим все члены, кроме B ₃ и Г ₃, в первую часть. Тогда

B ₃ + Г ₃ = 8 + (B ₅ + 2 B ₆ + 3 B ₇ +...) + (Г ₅ + 2 Г ₆ + 3 Г ₇ +...). (14)

Обе суммы в скобках неотрицательны. Поэтому

B ₃ + Г ₃ ³ 8.

Итак, у каждого выпуклого многогранника сумма числа треугольных граней и числа вершин степени 3 не меньше 8. В частности, он обязательно имеет треугольные грани или вершины степени 3, или те и другие вместе. Теперь умножим обе части равенства (12) на 2 и сложим с (13).Тогда

-(2 B ₄ + 4 B ₅ +...) + (3 Г ₃ + 2 Г ₄ + Г ₅) + (Г ₇ + 2 Г ₈ +...) = 12.

Или

3 Г ₃ + 2 Г ₄ + Г ₅ = 12 + (2 B ₄ + 4 B ₅ +...) + (Г ₇ + 2 Г ₈ +...). (15)

Так как обе суммы в скобках неотрицательны, то

3 Г ₃ + 2 Г ₄ + Г ₅ ³ 12. (16)

Неравенство (16) имеет интересные геометрические следствия. Оно показывает, что выпуклый многогранник обязательно имеет либо треугольные, либо четырехугольные, либо пятиугольные грани. В частности, не существует многогранника, у которого все грани были бы шестиугольными. Если предположить, что Г ₄ = Г ₅ = 0, то из (16) получаем Г ₃ ³ 4, и это неравенство точное, т. е. имеется многогранник, у которого Г ₄ = Г ₅ = 0 и Г ₃ = 4; это - тетраэдр. Если Г ₃ = Г ₅ = 0, то Г ₄ ³ 6; это неравенство тоже точное, как показывает пример куба. Если Г ₃ = Г ₄ = 0, то Г ₅ ³ 12; точность этого неравенства показывает пример додекаэдра (см. таблицу 1).

Неравенство, двойственное неравенству (16), имеет следующий вид:

3 B ₃ + 2 B ₄ + B ₅ ³ 12. (17)

Читатель сам сможет проверить его. Из (17) получаем, в частности, что не существует выпуклого многогранника, у которого все вершины имели бы степень, равную 6, а также следующие утверждения:

если B₄ = B ₅ = 0, то B ₃ ³ 4,

если B₃ = B ₅ = 0, то B ₄ ³ 6,

если B₃ = B ₄ = 0, то B ₅ ³ 12.

Три последних неравенства точные, что видно из таблицы 1.

Название многогранника	m	n	B	P	Г
Тетраэдр
Гексаэдр
Октаэдр
Додекаэдр
Икосаэдр

Выпуклый многогранник называется комбинаторно правильным, если все его грани имеют одинаковое число сторон (скажем m) и все его вершины имеют одинаковую степень (скажем n). Таким образом, в этом определении не требуется, чтобы грани были равными правильными многоугольниками или чтобы многогранные углы были равны. Этим комбинаторно правильный многогранник отличается от метрически правильного, известного из школьного курса геометрии (но, разумеется, метрически правильный многогранник является в то же время комбинаторно правильным.)

Будем говорить, что (комбинаторно правильный) многогранник имеет тип (m, n), если каждая его грань является m -угольником, а степень каждой вершины равна n.

Докажем, что может существовать только пять различных типов комбинаторно правильных многогранников. Мы уже знаем, что у правильного многогранника каждое из чисел m и n может быть равным только 3, или 4, или 5. Из этих чисел можно составить девять различных пар (m, n). Остается только проверить какие из этих девяти пар могут фактически осуществляться.

Итак, пусть имеется комбинаторно правильный многогранник типа (m, n). Тогда Г = Г_m и ввиду (11) 2 P = mГ. Аналогично, B = B_n и ввиду (10) 2 P = nP. Решая систему уравнений B - P + Г 2, 2 P = mГ, 2 P = nB относительно чисел B, P и Г, получаем

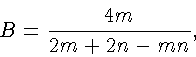
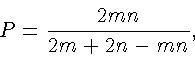
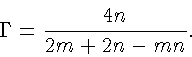
Так как эти числа положительны, то

2 m + 2 n - mn > 0

или

(m - 2)(n - 2) < 4. (18)

Теперь ясно, что из всех девяти пар чисел (m, n) неравенству (18) удовлетворяют только следующие пять

(3, 3), (4, 3), (3, 4), (5, 3), (3, 5).

Комбинаторно правильные многогранники, соответствующие таким парам, действительно существуют; они перечислены в таблице 1, где для них указаны значения чисел m, n, B, P и Г.

Из таблицы 1 видно, что для гексаэдра и октаэдра числа вершин одного из них равно числу граней другого и наоборот; тем самым эти многогранники двойственны друг другу. Аналогично - для додекаэдра и икосаэдра. Тетраэдр двойствен самому себе. Вообще можно было бы доказать, что для каждого выпуклого (не обязательно правильного) многогранника существует ему двойственный.