
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решения задач
|
|
1. Из условия задачи и из равенства (11) имеем 2 P = 3 Г, откуда следует первое утверждение. Исключая из равенств B - P + Г = 2 и 2 P = 3 Г сначала Г, затем P, получим требуемые равенства. Двойственная задача: если каждая вершина имеет степень 3, то число вершин четное.
2. Складывая равенства (14) и (15), получим
B 3 + 4 Г 3 + 2 Г 4 + Г 5 = 20 + Г 5 +..., (19)
где многоточие заменяет некоторые невыписанные неотрицательные члены, не содержащие чисел B 3 и Г 5. Если Г 3 = Г 4 = 0, то равенство (19) дает B 3 ³ 20 (пример - додекаэдр). Двойственная задача: если B 3 = B 4 = 0, то Г 3 ³ 20.
3. Из каждой вершины выходит B - 1 ребер. Поэтому общее число ребер равно 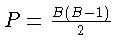 . Равенство (11) дает нам 3 Г £ 2 P. Подставим в это неравенство
. Равенство (11) дает нам 3 Г £ 2 P. Подставим в это неравенство 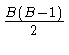 вместо P и
вместо P и 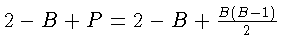 вместо Г (используя формулу Эйлера), тогда получаем
вместо Г (используя формулу Эйлера), тогда получаем
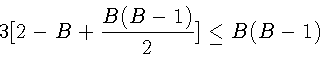
или
B 2 - 7 B + 12 £ 0.
Среди целых чисел решениями этого неравенства являются только B = 3 и B = 4.Так как многогранник не может иметь три вершины, то B = 4, т. е. многогранник является тетраэдром. Двойственная задача: если каждые две грани имеют общее ребро, то многогранник является тетраэдром.
4. Из неравенства 3 Г £ 2 P следует 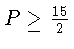 , т. е. P ³ 8. Из формулы Эйлера получаем B = P - 3. Тогда двойственное неравенство 3B £ 2 P дает 3(P - 3) £ 2 P, или P £ 9. Итак, допустимы только два значения: P = 8 и P = 9. В первом случае из формулы Эйлера получаем B = 5, во втором B = 6. Многогранником, у которого Г = 5, P = 8, B = 5, является, например, четырехугольная пирамида. Многогранником, у которого Г = 5, P = 9, B = 6, является, например, треугольная призма.
, т. е. P ³ 8. Из формулы Эйлера получаем B = P - 3. Тогда двойственное неравенство 3B £ 2 P дает 3(P - 3) £ 2 P, или P £ 9. Итак, допустимы только два значения: P = 8 и P = 9. В первом случае из формулы Эйлера получаем B = 5, во втором B = 6. Многогранником, у которого Г = 5, P = 8, B = 5, является, например, четырехугольная пирамида. Многогранником, у которого Г = 5, P = 9, B = 6, является, например, треугольная призма.
5. Пусть Г - общее число граней, и пусть n 1 - число ребер (или углов) у первой, n 2 - такое же число у второй,..., n G - такое же число у последней грани. Сумма всех углов всех граней равна
S = p(n 1 - 2) + p(n 2 - 2) +... + p(n G - 2) = p(n 1 + n 2 +... + n G - 2 Г).
Далее, общее число ребер у всех граней равно 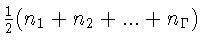 , и это число равно числу P ребер многогранника. Отсюда S = p(2 P - 2 Г). Заменяя P - Г по формуле Эйлера на B - 2, получаем
, и это число равно числу P ребер многогранника. Отсюда S = p(2 P - 2 Г). Заменяя P - Г по формуле Эйлера на B - 2, получаем
S = 2p(P - 2).
6. Мяч можно рассматривать как сферу, разбитую на сферические грани - многоугольники. При этом выполнены соотношения (1), (8)-(11) и все следствия из них, в частности, неравенство (16). Из него заключаем, что мяч нельзя сшить только из шестиугольных кусков.