
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача 3.1.2.
|
|
Часть 3. Случайные векторы.
Функция случайной величины
Задача 3.1.1. Дано распределение двумерного случайного вектора (ξ, η) с дискретными компонентами. Требуется:
1) Найти одномерные распределения случайных величин ξ и η, их математические ожидания M ξ, M η и дисперсии D ξ, D η;
2) Доказать независимость случайных величин ξ и η. Вычислить непосредственно их корреляционный момент Кξ η
Вариант 1 Вариант 2
| ξ \ η | -4 | -2 | ξ \ η | 0, 2 | 0, 8 | ||
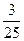
| 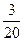
| 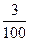
| -0, 4 | 0, 1 | 0, 15 | ||
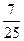
| 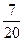
| 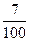
| 0, 4 | 0, 1 | 0, 15 | ||
| 0, 5 | 0, 2 | 0, 3 |
Вариант 3 Вариант 4
| ξ \ η | ||
| -8 | 0, 35 | 0, 15 |
| 0, 14 | 0, 06 | |
| 0, 21 | 0, 09 |
| ξ \ η | |||
| -4 | 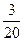
| 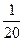
| 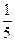
|
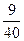
| 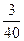
| 
|
Вариант 5 Вариант 6
| ξ \ η | -2 | ||
| 0, 3 | 
| 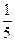
| 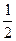
|
| 0, 4 | 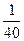
| 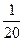
| 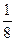
|
| ξ \ η | ||
| -10 | 0, 12 | 0, 28 |
| 0, 15 | 0, 35 | |
| 0, 03 | 0.07 |
| ξ \ η | ||
| -4 | 
| 
|
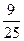
| 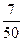
| |
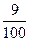
| 
|
Вариант 7 Вариант 8
| Вариант 8ξ \ η | -4 | ||
| -5 | 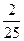
| 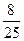
| 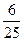
|
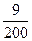
| 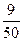
| 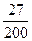
|
Вариант 9 Вариант 10
| ξ \ η | ||
| -6 | 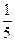
| 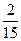
|
| -3 | 
| 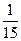
|

| 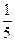
|
| ξ \ η | -2 | ||
| -1 | 0, 42 | 0, 07 | 0, 21 |
| 0, 18 | 0, 03 | 0, 09 |
Вариант 11 Вариант 12
| ξ \ η | |||

| 
| 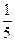
| |
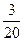
| 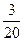
| 
|
| ξ \ η | -2 | ||
| 0, 35 | 0, 14 | 0, 21 | |
| 0, 15 | 0, 06 | 0, 09 |
Вариант 13 Вариант 14
| ξ \ η | -4 | ||
| -10 | 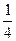
| 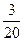
| 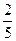
|
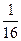
| 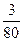
| 
|
| ξ \ η | -6 | |
| -4 | 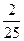
| 
|
| -3 | 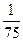
| 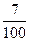
|
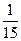
| 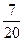
|
| ξ \ η | ||
| -40 | 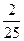
| 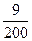
|
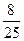
| 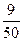
| |
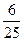
| 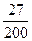
|
Вариант 15 Вариант 16
| ξ \ η | |||
| 0, 12 | 0, 15 | 0, 03 | |
| 0, 28 | 0, 35 | 0, 07 |
Вариант 17 Вариант 18
| ξ \ η | -2 | |
| -3 | 0, 42 | 0, 18 |
| -1 | 0, 07 | 0, 03 |
| 0, 09 | 0, 21 |
| ξ \ η | -20 | ||
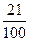
| 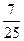
| 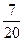
| |
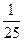
| 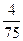
| 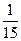
|
Вариант 19 Вариант 20
| ξ \ η | -6 | ||
| -2 | 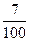
| 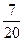
| 
|
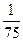
| 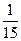
| 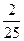
|
| ξ \ η | -2 | |

| 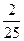
| |
| 1, 5 | 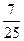
| 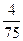
|
| 1, 8 | 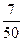
| 
|
Вариант 21 Вариант 22
| ξ \ η | ||
| -4 | 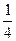
| 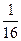
|
| 0, 15 | 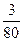
| |
| 0, 4 | 0, 1 |
| ξ \ η | -3 | -1 | |
| -2 | 0, 24 | 0, 36 | 0, 15 |
| 0, 08 | 0, 12 | 0, 05 |
| ξ \ η | -1 | |
| 0, 09 | 0, 16 | |
| 0, 18 | 0, 32 | |
| 0, 09 | 0, 16 |
Вариант 23 Вариант 24
| ξ \ η | -4 | -2 | |

| 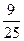
| 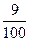
| |

| 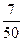
| 
|
Вариант 25 Вариант 26
| ξ \ η | -5 | |
| -4 | 
| 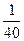
|
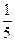
| 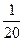
| |
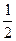
| 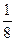
|
| ξ \ η | -12 | ||
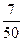
| 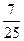
| 
| |

| 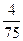
| 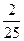
|
Вариант 27 Вариант 28
| ξ \ η | |||
| -1 | 0, 24 | 0, 36 | 0, 15 |
| 0, 08 | 0, 12 | 0, 05 |
| ξ \ η | |||
| -3 | 0, 09 | 0, 18 | 0, 09 |
| 0, 16 | 0, 32 | 0, 16 |
Вариант 29 Вариант 30
| ξ \ η | -4 | ||
| -2 | 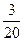
| 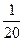
| 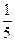
|
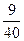
| 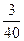
| 
|
| ξ \ η | ||
| -3 | 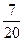
| 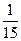
|
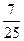
| 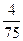
| |
| 0, 21 | 0, 04 |
Задача 3.1.2.
Вычислить математическое ожидание Мθ и дисперсию Dθ случайной величины θ двумя способами: на основании свойств математического ожидания и дисперсии и непосредственно – по ряду распределения θ.
Θ = α ξ + β η,
Где ξ, η – дискретные случайные величины из п. 3.1.1. N – номер варианта, α = N – 30, β = N.