
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Часть 5. Случайные процессы
|
|
Задача 5.1. Система имеет три состояния. Построить граф состояний системы, написать уравнения Колмогорова и найти стационарное распределение. λ ij – плотности перехода.
| № варианта | λ 12 | λ 13 | λ 21 | λ 23 | λ 31 | λ 32 |
Задача 5.2. Дана корреляционная функция и математическое ожидание случайного процесса ξ (t). Найти корреляционную функцию, математическое ожидание и дисперсию случайного процесса η (t).
| № варианта | Kξ (t1, t2) | Мξ (t) | η (t) |
| sin3t1 sin3t2 | e2t | td(ξ (t)+cost)/dt | |
| cos2t1 cos2t2 | sin3t | 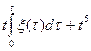
| |
| 2t13 t23 | 
| costdξ /dt+ e2t | |
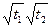 
| cos5t | t3 sin3t ξ (t)+ cost | |
| sin5t1 sin5t2 | t3 | 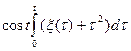
| |
| 3cos5t1 cos5t2 | e3t | 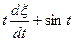
| |
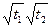 + sint1 sint2 + sint1 sint2
| t5 | t2 cos4t ξ (t)+ e3t | |
| t14 t24 | sin2t | 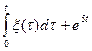
| |
2 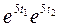
| cos3t |  sint (ξ (t)+t) sint (ξ (t)+t)
| |
| t13 t23+ cos3t1 cos3t2 | et | 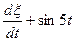
| |
| 2cos3t1 cos3t2 | e5t | td(ξ (t)+cost)/dt | |
| sin6t1 sin6t2 | 
| 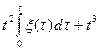
| |
5t13 t23 + 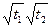
| sin4t | costdξ /dt+ e2t | |
3 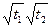 
| cos4t | t2 sin3t ξ (t)+t5 | |
| sin5t1 sin5t2+ t1 t2 | t3 | 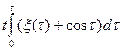
| |
| 3cos5t1 cos5t2 | e2t | 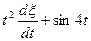
| |
| 5 sin7t1 sin7t2 | t5 | t cos2t ξ (t)+ et | |
t14 t24+ 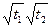
| sin2t | 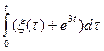
| |
7 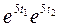
| t2 |  sint ξ (t)+cost sint ξ (t)+cost
| |
| 5 cos3t1 cos3t2 | e3t | 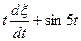
| |
| 9t1 t2 | e2t | t2d(ξ (t)+sint)/dt | |
| cos2t1 cos2t2 | cos4t | 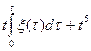
| |
| 2t13 t23+ sint1 sint2 | 
| costdξ /dt+ e2t | |
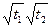 
| sin5t | t3 ξ (t)+t cost | |
| sin5t1 sin5t2 | t2 | 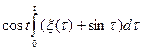
| |
| 4cos2t1 cos2t2 | e3t | 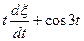
| |
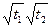 + sint1 sint2 + sint1 sint2
| cos4t | t cos4t ξ (t)+ e3t | |
| t14 t24 | sin3t | t 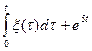
| |
2 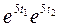
| cos6t |  sint (ξ (t)+t2) sint (ξ (t)+t2)
| |
| t13 t23+ cos3t1 cos3t2 | e2t | t2 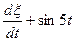
|
Задача 5.3. Найти корреляционную функцию и дисперсию случайного процесса ξ (t), если он задан каноническим разложением. Дисперсии случайных величин D ξ i = Di.
| № варианта | ξ (t) | D1 | D2 | D3 |
| ξ 1 sinω t+ ξ 2 cosω t+i ξ 3t3 | ||||
| 2 | ξ 1 e3it + ξ 2 e-3it + ξ 3t2 | |||
| 3 | iξ 1 sin2t+ ξ 2 + ξ 3t4 | |||
| 4 | 3ξ 1 t+ ξ 2 cos5t+i ξ 3t2 
| |||
| 5 | ξ 1 sinω t+ ξ 2 cosω t+2i ξ 3t5 | |||
| 6 | ξ 1 e4it + ξ 2 e-4it + ξ 3 cosω t | |||
| 7 | ξ 1 e3t +5i ξ 2 t + ξ 3 | |||
| 8 | ξ 1 sin2t+ iξ 2 cos3t+ ξ 3t2 | |||
| 9 | ξ 1 e5it + ξ 2 t3+ ξ 3 sinω t | |||
| 10 | ξ 1 + ξ 2 te2t + 3iξ 3cost | |||
| 11 | ξ 1 sinω t+ ξ 2 cosω t+2i ξ 3t4 | |||
| 12 | ξ 1 e5it + ξ 2 e-5it + ξ 3t4 | |||
| 13 | iξ 1 cos2t+ ξ 2 + ξ 3t5 | |||
| 14 | 4ξ 1 t2+ ξ 2 sin5t+i ξ 3t 
| |||
| 15 | ξ 1 sinω t+ ξ 2 cosω t+2i ξ 3t6 | |||
| 16 | ξ 1 e7it + ξ 2 e-7it + ξ 3 cos2t | |||
| 17 | ξ 1 e2t +5i ξ 2 t5 + ξ 3 | |||
| 18 | ξ 1 sint+ iξ 2 cos4t+ ξ 3t3 | |||
| 19 | ξ 1 e4it + ξ 2 t7+ ξ 3 cosω t | |||
| 20 | ξ 1 + ξ 2 te2t + 3iξ 3sint | |||
| 21 | ξ 1 sinω t+ ξ 2 cosω t+ie2t | |||
| 22 | ξ 1 e3it + ξ 2 e-3it + ξ 3tcost | |||
| 23 | 2iξ 1 t+ ξ 2 + ξ 3t4sint | |||
| 24 | 5ξ 1 t3+ ξ 2 cos2t+i ξ 3t6 
| |||
| 25 | ξ 1 sinω t+ ξ 2 cosω t+3i ξ 3t3 | |||
| 26 | ξ 1 e4it + ξ 2 e-4it + ξ 3 tcos8t | |||
| 27 | ξ 1 te3t +5i ξ 2 t + ξ 3 | |||
| 28 | ξ 1 sint+ iξ 2 cos4t+ ξ 3t4 | |||
| 29 | ξ 1 e5it +i ξ 2 t3+ ξ 3 cos2t | |||
| 30 | ξ 1 + ξ 2 te2t + 3iξ 3sin2t |
Задача 5.4. Найти одностороннюю S(ω) и двустороннюю S*(ω) спектральную плотность стационарного случайного процесса с корреляционной функцией 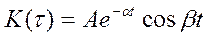
| № варианта | α | Β | A | № варианта | α | Β | A |
Задача 5.5. Работа динамической системы описывается уравнением 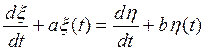 . На вход системы поступает стационарный процесс ξ (t) с корреляционной функцией
. На вход системы поступает стационарный процесс ξ (t) с корреляционной функцией 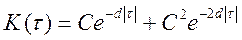 . Найти дисперсию процесса на выходе системы.
. Найти дисперсию процесса на выходе системы.
| № варианта | a | b | C | D |