
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Модуль 2. Случайные величины
|
|
11.15. Дискретная случайная величина X задана законом распределения:
| X | ||||
| р | 0, 2 | 0, 1 | 0, 4 | 0, 3 |
Построить многоугольник распределения.
Решение. Построим прямоугольную систему координат, причем по оси абсцисс будем откладывать возможные значения xi, а по оси ординат—соответствующие вероятности рi. 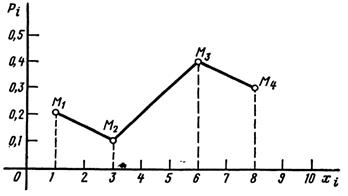
Построим точки M1(1; 0, 2), M2 (3; 0, 1), M3 (6; 0, 4) и M4 (8; 0, 3). Соединив эти точки отрезками прямых, получим искомый многоугольник распределения.
11.16. Найти математическое ожидание дискретной случайной величины X, заданной законом распределения:
а) X - 4 6 10
р 0, 2 0, 3 0, 5 •
Решение Математическое ожидание равно сумме произведений всех возможных значений X на их вероятности:
М (X) = ~ 4 0, 2 + 6 0, 3 +10 0, 5 = 6.
(М (X) = X1P1 + X2P2+ *.. +ХпРп).
11.17. Найти дисперсию и среднее квадратическое отклонение дискретной случайной величины X, заданной законом распределения:
X —5 2 3 4
р 0, 4 0, 3 0, 1 0, 2
Решение. Дисперсию можно вычислить исходя из ее определения, однако мы воспользуемся формулой 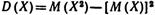
Найдем математическое ожидание X:
М (X) = —5.0.4 + 2 0. 3 + 3.0.14-4.0.2 = –.0, 3.
Напишем закон распределения Х2:
Х2 25 4 9 16
р 0, 4 0, 3 0.1 0, 2
Найдем математическое ожидание Х:
M(Х2)=25*0, 4 + 4*0, 3 + 9*0, 1 + 16*0, 2=15, 3,
Найдем искомую дисперсию:
D(X) = M(Х2)— [M(X)]2 = 15, 3—(—0, 3)2 ==15, 21.
Найдем искомое среднее квадратическое отклонение:
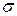 (X) ==
(X) == 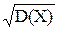 =
= 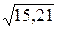 =3, 9
=3, 9
11.18. Дискретная случайная величина X задана законом распределения
X 2 4 7
Р 0, 5 0, 2 0, 3
Найти функцию распределения F (х) и начертить ее график.
Решение.
1. Если x 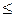 2, то р(х)=0. Действительно, значений, меньших числа 2, величина X не принимает. Следовательно,
2, то р(х)=0. Действительно, значений, меньших числа 2, величина X не принимает. Следовательно,
при x 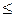 2 функция F(x)=: P (X < 2) = 0.
2 функция F(x)=: P (X < 2) = 0.
2. Если 2 < x 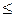 4, то F(x) = 0, 5. Действительно, X может принять значение 2 с вероятностью 0, 5.
4, то F(x) = 0, 5. Действительно, X может принять значение 2 с вероятностью 0, 5.
3. Если 4 < x 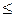 7, то F(x)=0, 7. Действительно, X может принять значение 2 с вероятностью 0, 5 и значение 4 с вероятностью 0, 2; следовательно, одно из этих значений, безразлично какое, X может принять (по теореме сложения вероятностей несовместных событий) с вероятностью 0, 5 + 0, 2 = 0, 7.
7, то F(x)=0, 7. Действительно, X может принять значение 2 с вероятностью 0, 5 и значение 4 с вероятностью 0, 2; следовательно, одно из этих значений, безразлично какое, X может принять (по теореме сложения вероятностей несовместных событий) с вероятностью 0, 5 + 0, 2 = 0, 7.
4. Если x > 7, то F(х) = 1. Действительно, событие Х< 7 достоверно
и вероятность его равна единице.
Итак, искомая функция распределения имеет вид
F(x)= 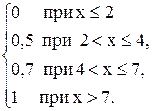
|
11.19. Дана функция распределения непрерывной случайной величины X
F {х) = 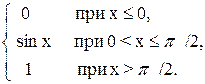
Найти плотность распределения f(x).
Решение. Плотность распределения равна первой производной от функции распределения:
f {х) = 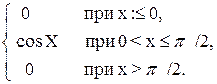
Заметим, что при х=0 производная F' (x) не существует.
11.20 Задана плотность распределения непрерывной случайной величины X:
f(x)= 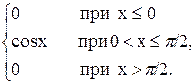
Найти функцию распределения F{x).
Решение, Используем формулу
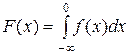
Если х 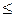 < 0, то f{x)=0, следовательно,
< 0, то f{x)=0, следовательно,
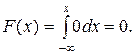
Если 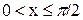 , то
, то
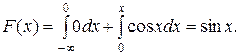
Если 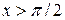 , то
, то
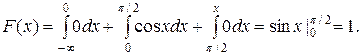
Итак, искомая функция распределения
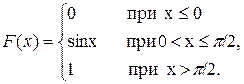 268.
268.