
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Модуль 3 Математическая статистика
|
|
(Цылова Е. Г., Кротова Е. Л.ПГТУ, 2007)
11.21. Даны 5 наблюдений над случайной величиной скорости автомобилей на одном из участков шоссе (км/ч): 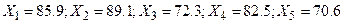 . Требуется построить доверительный интервал для математического ожидания
. Требуется построить доверительный интервал для математического ожидания 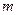 при
при 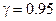 , когда дисперсия
, когда дисперсия 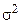 - неизвестна. Как изменится доверительный интервал, если при тех же значениях средней скорости и выборочной дисперсии число наблюдений возрастет в 10 раз?
- неизвестна. Как изменится доверительный интервал, если при тех же значениях средней скорости и выборочной дисперсии число наблюдений возрастет в 10 раз?
Решение. Из условия известно, что 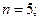
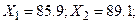
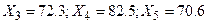 . По имеющимся данным вычислим:
. По имеющимся данным вычислим:
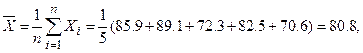
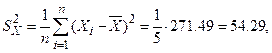
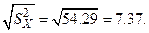
По таблице 4 приложения находим, что при 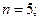
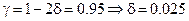 и
и 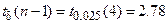 . Вычислим доверительный интервал:
. Вычислим доверительный интервал:
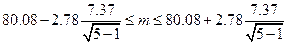 ;
;
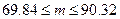
Получили доверительный интервал для скорости, которую можно ожидать на данном участке шоссе.
Если число наблюдений возрастет в 10 раз (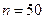 ), вновь воспользуемся той же формулой для построения интервала. По таблице 4 приложения находим, что
), вновь воспользуемся той же формулой для построения интервала. По таблице 4 приложения находим, что 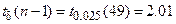 . Тогда
. Тогда
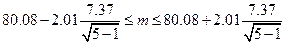 ;
;
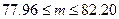 .
.
11.22 Социологические обследования дали следующие результаты. Из 1000 опрошенных людей 849 никогда не обращались за юридической консультацией, из них 649 занимаются предпринимательской деятельностью, а 200 работают на государственных предприятиях. И из 151 обращавшегося респондента 101 человек занимался предпринимательской деятельностью, а 50 – нет. По имеющимся данным: 1) построить таблицу сопряженности; 2) оценить условные и безусловные вероятности признаков; 3) оценить тесноту связи между признаками; 4) при уровне значимости 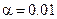 проверить нулевую гипотезу о независимости исследуемых признаков; 5) изменится ли характер зависимости, если все данные увеличить в 25 раз?
проверить нулевую гипотезу о независимости исследуемых признаков; 5) изменится ли характер зависимости, если все данные увеличить в 25 раз?
Решение. 1. Пусть признак A – человек занимается предпринимательской деятельностью; признак B – человек обращался за юридической консультацией. Тогда, согласно условию: 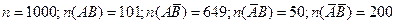 и таблица сопряженности имеет вид
и таблица сопряженности имеет вид
| Признаки | 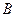
| 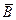
| Всего |

| |||
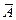
| |||
| Всего |
2. Вычислим оценки условных и безусловных вероятностей.
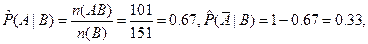
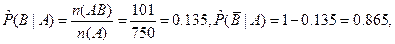
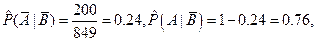
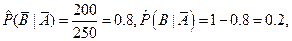
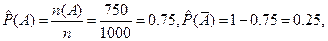
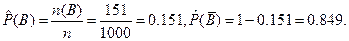
3. Тесноту связи между признаками оценим, вычислив эмпирический коэффициент корреляции событий
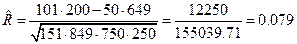 .
.
Так как полученное значение коэффициента 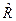 мало, можно предположить, что зависимость между A и B практически отсутствует.
мало, можно предположить, что зависимость между A и B практически отсутствует.
4. Найдем значение статистики 
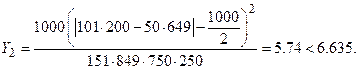
Из таблицы 3 приложения нашли при 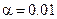
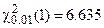 . Учитывая, что
. Учитывая, что  нулевая гипотеза принимается и делается вывод – обращение за юридической консультацией не зависит от того занимается ли человек своим бизнесом или работает на государственном предприятии.
нулевая гипотеза принимается и делается вывод – обращение за юридической консультацией не зависит от того занимается ли человек своим бизнесом или работает на государственном предприятии.
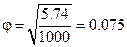 .
.
5. При увеличении данных в 25 раз опять подсчитаем статистику
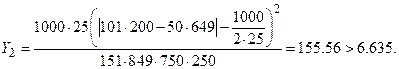
Следовательно, нулевая гипотеза отвергается, что говорит о наличии связи между признаками, оценим тесноту связи:
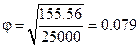 ,
,
Теснота связи между A и B остается прежней, ее значения не зависят от числа наблюдений.
11.23 Случайная величина 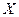 - число лет, которые служащие проработали в торговой компании;
- число лет, которые служащие проработали в торговой компании; 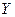 - сколько отпусков за это время они брали в этой компании. Результаты наблюдений над случайными величинами
- сколько отпусков за это время они брали в этой компании. Результаты наблюдений над случайными величинами 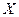 и
и 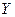 : приведены в следующей таблице:
: приведены в следующей таблице:
| X | 2 | 3 | 4 | 5 |
| Y | 3 | 4 | 6 | 8 |
Построить уравнения прямых регрессий 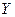 по
по 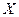 и
и 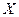 по
по 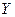 . Найти выборочный коэффициент линейной корреляции
. Найти выборочный коэффициент линейной корреляции 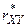 .
.
Решение. Из условия находим:
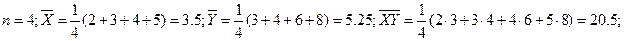
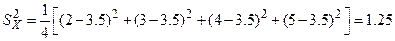 ;
;
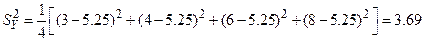 ;
;
Воспользовавшись предложенными формулами, вычислим коэффициенты прямых регрессий 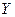 по
по 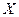 и
и 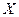 по
по 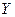 .
.
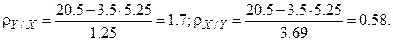
И по формулам построим уравнения прямых регрессий и выборочный коэффициент линейной корреляции.
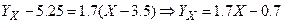 ;
;
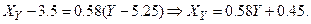
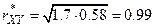 .
.
11.24 При обработке наблюдений из 900 торговых точек за количеством проданных шампуней и соответствующих им лечебных бальзамов был найден выборочный коэффициент линейной корреляции  . По имеющимся данным построить доверительный интервал для коэффициента линейной корреляции
. По имеющимся данным построить доверительный интервал для коэффициента линейной корреляции  с доверительной вероятностью
с доверительной вероятностью 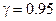 .
.
Решение. По таблице приложения 2 находим для 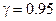 соответствующее значение
соответствующее значение 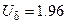 . Согласно формуле доверительный интервал выглядит следующим образом:
. Согласно формуле доверительный интервал выглядит следующим образом:
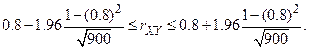
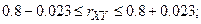
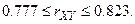
Следовательно, при заданной доверительной вероятности истинное значение  может варьировать в пределах от 0, 777 до 0, 823 и зависимость между случайными величинами
может варьировать в пределах от 0, 777 до 0, 823 и зависимость между случайными величинами 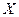 и
и 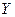 сильная.
сильная.
11.25 По выборке 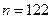 найден выборочный коэффициент линейной корреляции
найден выборочный коэффициент линейной корреляции 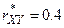 . При уровне значимости
. При уровне значимости 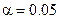 проверить нулевую гипотезу о равенстве нулю коэффициента линейной корреляции
проверить нулевую гипотезу о равенстве нулю коэффициента линейной корреляции 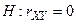 против
против 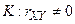 .
.
Решение. Известно, что 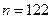 ,
, 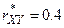 . Вычислим статистику
. Вычислим статистику  :
:
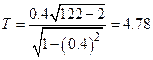 .
.
Из таблицы приложения 4 находим, что при 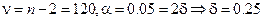 , значение критической точки распределения Стьюдента
, значение критической точки распределения Стьюдента 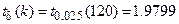 . Поскольку 4, 78> 1, 9799, то есть
. Поскольку 4, 78> 1, 9799, то есть  , то нулевая гипотеза отвергается, величины
, то нулевая гипотеза отвергается, величины 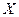 и
и 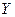 зависимы, поскольку
зависимы, поскольку 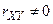 .
.
11.26. Даны выборочные варианты х1 и соответствующие им частоты ni количественного признака Х. а) найти выборочные среднюю дисперсию и среднеквадратическое отклонение. б) Считая, что количественный признак Х распределен по нормальному закону и что выборочная дисперсия равна генеральной дисперсии, найти доверительный интервал для оценки математического ожидания с надежностью γ =0, 99
| хi | 10, 2 | 15, 2 | 20, 2 | 25, 2 | 30, 2 | 35, 2 | 40, 2 |
| ni |
Р ешение
1. Объем выборки
n= 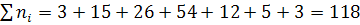
Средняя выборочная:
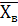 =
= 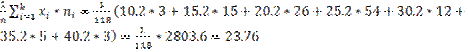
Выборочная дисперсия:
Dв= 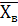 2 –
2 – 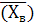 2, где
2, где 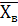 =23, 76
=23, 76
Средняя выборочная квадратов значений признака γ
 =
= 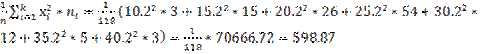
Тогда Dв=598, 87-(23, 76)2=34, 33
Среднее квадратичное отклонение:
σ в= 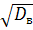 σ в=
σ в= 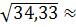 5, 86
5, 86
пусть количественный признак Х генеральной совокупности распределен по нормальному закону, причем среднеквадратическое значение отклонение «σ» этого распределения известно. Тогда с вероятностью γ доверительный интервал заданный формулой
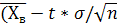 ;
; 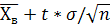 ),
),
покрывает неизвестное математическое ожидание. Здесь число t находится из соотношения 2Ф(t)=γ с помощью таблицы интегральной функции Лапласса.
В данной задаче γ =0, 99, поэтому 2Ф(t)=0, 99, а Ф(t)=0, 495, по таблице находим t=2, 58.
По условию задачи дисперсия генеральной совокупности D=Dв и, следовательно, σ =σ в=5, 86. ранее найдены значения n=118, и Хв=23, 76. Поэтому можно найти доверительный интервал:
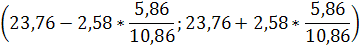
(23, 76-1, 39; 23, 76+1, 39)
(22, 37; 25, 15).
Ответ: Хв=23, 76; Dв=34, 33; σ в=5, 86; а 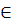 (22, 37; 25, 15).
(22, 37; 25, 15).
11.27. По данным корреляционной таблицы найти условные средние Yx и Xy. Оценить тесноту линейной связи между признаками X и Y и составить уравнение линейной регрессии Y по X и X по Y. Сделать чертеж, нанеся на него условные средние и найденные прямые регрессии. Оценить силу связи между признаками с помощью корреляционного отношения.
| Y\X | Ny | ||||||
| Nx | n=100 |
Найдем условные средние воспользовавшись формулами:
Ү x=  Xy=
Xy= 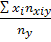
Yx=5= 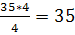 Xy=35=
Xy=35= 
Yx=10= 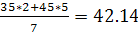 Xy=45=
Xy=45= 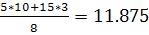
Yx=15= 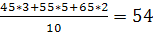 Xy=55=
Xy=55= 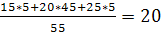
Yx=20= 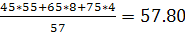 Xy=65=
Xy=65= 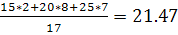
Yx=25 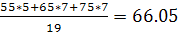 Xy=75=
Xy=75= 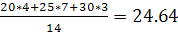
Yx=30 
Оценка тесноты линейной связи между признаками X и Y производится с помощью коэффициента линейной корреляции r:

Коэффициент r может принимать значения от -1 до +1.
Знак r указывает на вид связи: прямая или обратная. Абсолютная величина |r| на тесноту связи. При r> 0 связь прямая, то есть с ростом х растет у.
При r< 0 связь обратная, то есть с ростом х убывает у.
Для нахождения rвычислим указанные общие средние: х, у, ху, а также средние квадратические отклонения σ х и σ у. Вычисления удобно поместить в таблицах, куда вписываем также найденные ранее условные средние.
Значение коэффициента линейной корреляции
| Х | nx | x*nx | x2*nx |  yx yx
|  x*nx*yx x*nx*yx
|
| 42.14 | 2949.8 | ||||
| 57.8 | |||||
| 66.05 | 31373.75 | ||||
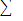
| - | 115765.55 |
| Y | ny | y*ny | y2*ny |  xy xy
|  y*ny*xy y*ny*xy
|
| 6.67 | 1400.7 | ||||
| 11.875 | |||||
| 21.47 | 23724.35 | ||||
| 24.64 | |||||
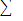
| - | 115772.05 |
С помощью таблиц находим общие средние, средние квадратов, среднюю произведения и среднеквадратические отклонения:
Х= 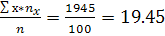
X2= 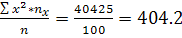 5
5
XY= 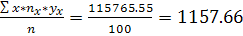
Y= 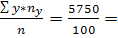 57.5
57.5
Y2= 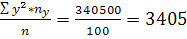
 σ x=
σ x= 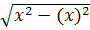 =
= 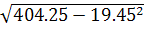 =
= 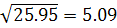
 σ y=
σ y= 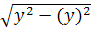 =
= 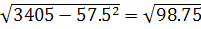 =9.94
=9.94
Отсюда коэффициент корреляции равен:
r= 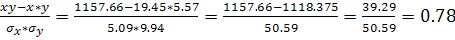
т.к r > 0, то связь прямая, то есть с ростом Х растет Y.
т.к | r | > 0, 78 то линейная связь высокая.
Находим линейное уравнение регрессии Y по X:
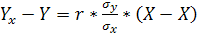
Yx-57.5=0.78* 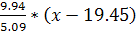
Yx=1.52x+27.94
Аналогично находим уравнение регрессии X поY:

Xy-19.45=0.78* 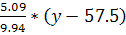
Xy=0.4y-3.55
Данные уравнения устанавливают связь между признаками X и Y и позволяют найти среднее значение признака Yx для каждого значения x и аналогично среднее значение признака Xy для каждого значения y.
Изобразим полученные результаты графически.
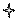 Нанесем на график точки (х; ух) отметив их звездочками(). Нанесем на график точки (ху; у) отметив их кружочками (). Построим каждое из найденных уравнений регрессии по двум точкам:
Нанесем на график точки (х; ух) отметив их звездочками(). Нанесем на график точки (ху; у) отметив их кружочками (). Построим каждое из найденных уравнений регрессии по двум точкам:
| х | ||
| у | 35, 54 | 73, 54 |
Yx=1.52x+27.94
| х | 10, 45 | 26, 45 |
| у |
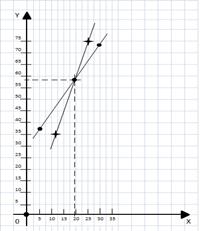 Xy=0.4y-3.55
Xy=0.4y-3.55
Обе прямые регрессии пересекаются в точке (х; у). В нашей задаче это точки (19, 45; 57, 5).
Оценка тесноты любой связи между признаками производится с помощью корреляционных отношений Y по X и X по Y:
η ух= 
Дисперсия 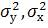 называемые внутригрупповыми, определены ранее.
называемые внутригрупповыми, определены ранее.
Величины 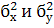 называются межгрупповыми дисперсиями и вычисляются по формулам:
называются межгрупповыми дисперсиями и вычисляются по формулам:




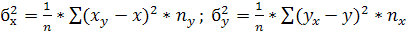
Они характеризуют разброс условных средних, от общей средней. В данной задаче:
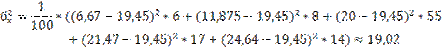

бх= 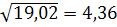
бу= 
Тогда корреляционные отношения равны:
η ух= 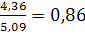
η ху= 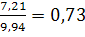
Ответ: Корреляционная связь между признаками высокая ее можно описать уравнениями:
Yx=1.52x+27.94,
Xy=0.4y-3.55.