
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Приближение функций
|
|
Из всех вопросов темы 1.4. Приближение функций изучается лишь метод наименьших квадратов. Вопросы этой темы не содержатся в контрольной работе, поэтому здесь приводятся только основные теоретические положения.
Метод наименьших квадратов
Пусть известно, что величины 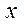 и
и 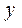 связаны некоей функциональной зависимостью. Требуется приближенно определить эту функциональную зависимость
связаны некоей функциональной зависимостью. Требуется приближенно определить эту функциональную зависимость 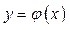 по экспериментальным данными. Предположим, что в результате
по экспериментальным данными. Предположим, что в результате 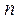 измерений получен ряд экспериментальных точек
измерений получен ряд экспериментальных точек  . Мы уже знаем, что через
. Мы уже знаем, что через 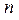 точек всегда можно провести кривую, аналитически выражаемую многочленом
точек всегда можно провести кривую, аналитически выражаемую многочленом 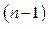 - ой степени. Этот многочлен называют интерполяционным. Вообще, замену функции
- ой степени. Этот многочлен называют интерполяционным. Вообще, замену функции 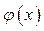 на функцию
на функцию 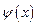 так, что их значения совпадают в заданных точках
так, что их значения совпадают в заданных точках
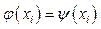 ,
, 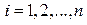 , (1)
, (1)
называют интерполяцией.
Однако такое решение проблемы не всегда является удовлетворительным, поскольку 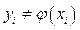 из-за случайных ошибок измерения и, возможно, случайной природы самих величин x и y. Т.о., можно записать, что
из-за случайных ошибок измерения и, возможно, случайной природы самих величин x и y. Т.о., можно записать, что
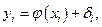 (2)
(2)
где 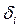 – некоторая случайная ошибка. Поэтому требуется провести кривую так, чтобы она в наименьшей степени зависела от случайных ошибок. Эта задача называется сглаживанием (аппроксимацией) экспериментальной зависимости и часто решается методом наименьших квадратов. Сглаживающую кривую называют аппроксимирующей.
– некоторая случайная ошибка. Поэтому требуется провести кривую так, чтобы она в наименьшей степени зависела от случайных ошибок. Эта задача называется сглаживанием (аппроксимацией) экспериментальной зависимости и часто решается методом наименьших квадратов. Сглаживающую кривую называют аппроксимирующей.
Задача аппроксимации решается следующим образом. В декартовой прямоугольной системе координат наносят точки 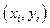 . По виду расположения этих точек делается предположение о принадлежности искомой функции к определенному классу. Например, линейная
. По виду расположения этих точек делается предположение о принадлежности искомой функции к определенному классу. Например, линейная 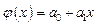 , квадратичная
, квадратичная 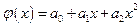 и т.п. В общем случае
и т.п. В общем случае 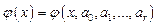 . Неизвестные параметры функции
. Неизвестные параметры функции 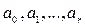 определяются из требования минимума суммы квадратов случайных ошибок, т.е. минимума величины
определяются из требования минимума суммы квадратов случайных ошибок, т.е. минимума величины
 . (3)
. (3)
Величина 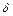 называется также суммарной невязкой. Необходимым условием минимума функции нескольких переменных является обращение в нуль частных производных невязки:
называется также суммарной невязкой. Необходимым условием минимума функции нескольких переменных является обращение в нуль частных производных невязки:
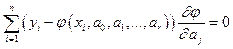 ,
, 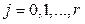 . (4)
. (4)
Решая систему уравнений (4), находят неизвестные параметры 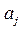 и тем самым полностью определяют функцию, которая наилучшим образом (в смысле наименьших квадратов отклонений от исходных точек или наименьшей суммарной невязки) аппроксимирует искомую функцию
и тем самым полностью определяют функцию, которая наилучшим образом (в смысле наименьших квадратов отклонений от исходных точек или наименьшей суммарной невязки) аппроксимирует искомую функцию 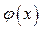 .
.
Рассмотрим подробнее линейную зависимость 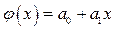 .
.
Дифференцируя (3), получим следующую систему уравнений
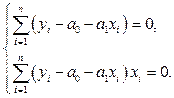 (5)
(5)
Из первого уравнения находим 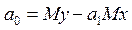 , где
, где
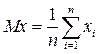 ,
,  . (6)
. (6)
Подставляя выражение для 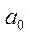 во второе уравнение, найдем
во второе уравнение, найдем
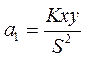 , (7)
, (7)
где
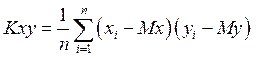 ,
, 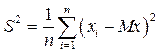 . (8)
. (8)
Таким образом,
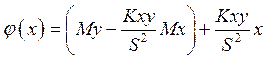 (9)
(9)
есть искомая линейная функция.
Ввиду простоты расчетов аппроксимация линейной зависимости используется довольно часто. Кроме того, многие функции, зависящие от двух параметров, можно линеаризовать путем замены переменных.
Для этого необходимо подобрать такое преобразование исходной зависимости 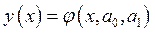 , в результате которого она приобретает линейный вид
, в результате которого она приобретает линейный вид 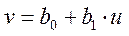 . Далее решается задача линейной аппроксимации для новой зависимости и вычисленные коэффициенты
. Далее решается задача линейной аппроксимации для новой зависимости и вычисленные коэффициенты 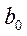 и
и  пересчитываются в коэффициенты
пересчитываются в коэффициенты 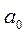 и
и  .
.
Для ряда часто встречающихся двухпараметрических зависимостей возможные замены переменных (а также, обратные замены для пересчета 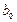 и
и 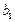 в
в 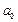 и
и 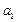 ) приведены в табл. 1.
) приведены в табл. 1.
Таблица 1.
| Вид зависимости | Замена переменных | Ограничения | Обратная замена переменных | ||
Гиперболическая
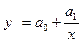
|

| 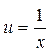
| 
|
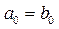
| 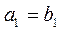
|
Логарифмическая
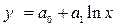
|

| 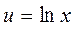
| 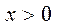
|
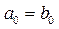
| 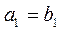
|
Показательная
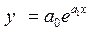
|
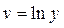
| 
| 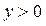
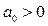
| 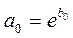
| 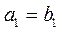
|
Степенная
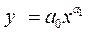
| 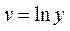
| 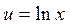
|  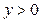 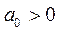
| 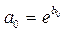
| 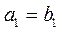
|
Комбинированная
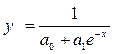
| 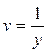
| 
| 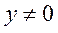
| 
| 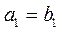
|
Более полное изложение этой темы – в [7], c.164-200.
Вопросы для самопроверки по теме 1.4
1. Что называется суммарной невязкой?
2. В чём состоит условие минимума функции нескольких переменных?