Метод трапеций

Для получения формулы трапеций интервал интегрирования [ a, b ] разбивается на n подынтервалов равной длины (шагов) точками: x ₀ = a, x ₁, x ₂, …, x_i, x_{i +1}, …, x_n = b так, что

x_{i +1} - x_i = h = 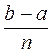, i = 1, 2, …, n.

На каждом отрезке (x_i, x_{i +1}) дугу X_i X_{i +1} графика подынтегральной функции y = f (x) заменяют стягивающей ее хордой (рис. 2.5) и вычисляют площади трапеций x_iX_i X_{i +1} x_{i +1}, высота которых равна h, а основания определяются значением функции f (x_i), f (x_i+1).

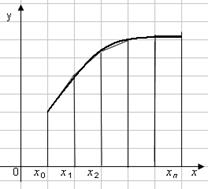
Рис. 2.5

Так как площадь трапеции равняется полусумме оснований, умноженной на высоту, интеграл приближенно равен сумме площадей всех полученных трапеций:

=

= =

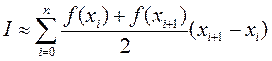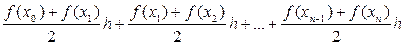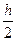= [ f (x ₀) + 2 f (x ₁) + 2 f (x ₂)+…+ + 2 f (x_{n- 1}) + f (x_n)]=

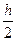= [ f (x_a) + 2 f (x ₁) + 2 f (x ₂)+…+ + 2 f (x_{n- 1}) + f (x_b)]=

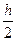= [ f (x_a) + f (x_b) + 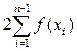]. (7)

Таким образом, формула трапеций имеет вид:

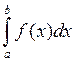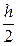
I = ≈ 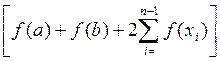. (8)

Точность интегрирования для этого метода приближенно равняется ε ≈ h².

Пример (продолжение). □ Пользуясь формулой трапеций, вычислить 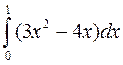при h = 0, 2.

Решение. Вычисление интеграла 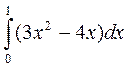методом трапеций (8) выполним в таблице Excel (рис. 6, 6- а).

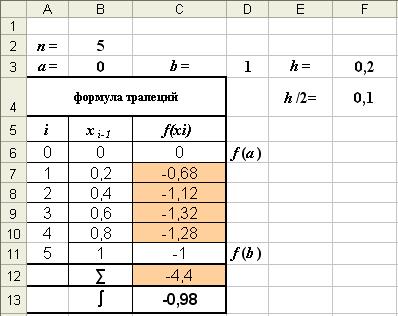
Режим решения

Рис. 6

∑ = -0, 68 -1, 12 -1, 32 -1, 28 = -4, 4 I = 0, 1·[(0-1)-2·4, 4] = -0, 98

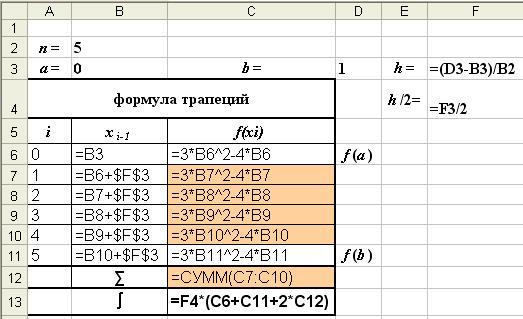
Режим показа формул

Рис. 6 - а

Разбивая интервал интегрирования на большее число отрезков, например, на 10, можно получить более точное решение (рис. 7).

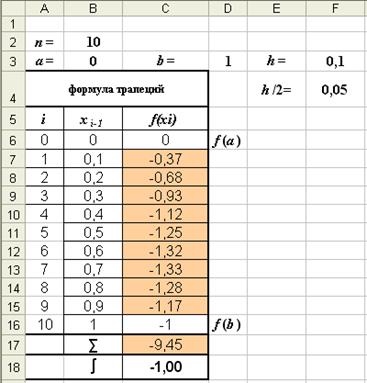
Рис. 7