Основные теоретические положения. Решить дифференциальное уравнение y' = f(x, y) численным методом –значит для заданной последовательности аргументов x0

Решить дифференциальное уравнение y ' = f (x, y) численным методом –значит для заданной последовательности аргументов x ₀, x ₁, …, x_n и числа y ₀, не определяя функцию y = F (x), найти такие значения у ₁, у ₂, …, y_n, что y_i = F (x_i) (i = 1, 2, …, n) и F (x ₀) = y ₀. Другими словами, численные методы позволяют вместо нахождения функции y = F (x), получить таблицу значений этой функции для заданной последовательности аргументов. Величина h = x_k – x_{k -1} называется шагом интегрирования.

Для решения данной задачи используются различные численные методы, среди которых наиболее простым является метод Эйлера.

Пусть дано дифференциальное уравнение первого порядка

y ' = f (x, y) (1)

с начальными условиями

x = x ₀, у (x ₀) = y ₀.

Требуется найти решение уравнения (1) на отрезке [ a, b ].

Разобьем отрезок [ a, b ] на n равных частей и получим последовательность x ₀, x ₁, …, x_n, где x_i = x ₀ + i·h (i = 1, 2, …, n), а h = (b – a)/ n – шаг сетки. Величина h = ∆ x_m = x_m+1 - x_i обычно выбирается постоянной и достаточно малой. При численном решении задачи вычисляются приближенные значения y_i (x_i) ≈ y_i в узлах сетки x_i (i = 1, 2, …, n).

Идея метода состоит в том, что при малом шаге сетки h производная искомой функции y' (x_i)может быть приближенно заменена конечными разностями

(2)

где y_i – значение функции в узле x_i.

Тогда y '(x_i)∙ h = y_i+1 - y_i, отсюда y_i+1 = y_i+ y '(x_i)∙ h, а, так как y '(x_i) = f (x_i, y_i), то

y_{i +1} = y_i + h·f (x_i, y_i). (3)

Т.е. на каждом отрезке [ x_i, x_i+1 ] выражение (1) можно заменить приближенным выражением (3).

Зная начальное значение y ₀, и используя соотношение (3), можно последовательно от узла x_i к узлу x_{i +1} определить все искомые значения y_{i +1}.

На практике, как правило, применяют «двойной просчет». Сначала расчет ведется с шагом h, затем шаг дробят и повторный расчет ведется с шагом h /2 и

т.д.

Для достижения требуемой точности ε численного решения необходимо выполнение условия: | y _{2 n} - y_n | < ε.

Пример 1. ○ Используя метод Эйлера, составить на отрезке [0, 1] таблицу значений решения дифференциального уравнения

с начальными условиями x ₀ = 0, y ₀ = 1, выбрав шаг h = 0, 2.

Решение.

Результаты вычислений представим в таблице Excel (рис.1). Заполняется она следующим образом:

1) В первую строку, соответствующую значению i = 0, запишем начальные условия: x ₀ = 0, y ₀ = 1. По ним вычислим значение f (x ₀, y ₀):

а затем значение ∆ y ₀. Из (2) и (1) имеем

∆ y ₀ = y '(x ₀)∙ ∆ x ₀ = y' (x ₀) ∙ h = f (x ₀, y ₀) ∙ h,

следовательно, ∆ y ₀ = h∙ f (x ₀, y ₀) = 0, 2∙ 1 = 0, 2. Отсюда по формуле (3) для i = 0 получим

y ₁ = y ₀ + h∙ f (x ₀, y ₀) = y ₀+ ∆ y ₀ = 1 + 0, 2 = 1, 2.

2) Значение x ₁ = x ₀ + h = 0 + 0, 2 = 0, 2 и соответствующее ему значение y ₁ =1, 2 запишем во вторую строку таблицы, соответствующую i = 1.

Для x ₁ = 0, 2 и y ₁ = 1, 2 вычислим f (x ₁, y ₁).

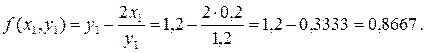
Затем вычислим ∆ y ₁ = h∙ f (x ₁, y ₁) = 0, 2∙ 0, 8667 = 0, 1733.

Тогда по формуле (3) для i = 1 получим

y ₂ = y ₁ + h∙ f (x ₁, y ₁) = y ₁+ ∆ y ₁ = 1, 2 + 0, 1733 = 1, 3733.

3) Значения x ₂ = x ₁ + h = 0, 2 + 0, 2 = 0, 4 и соответствующее ему значение y ₂ =1, 3733 запишем в третью строку таблицы (i = 2).

Аналогично следует выполнить вычисления для i = 2, 3, 4, 5 (см. рис. 1).● ○

Режим формул

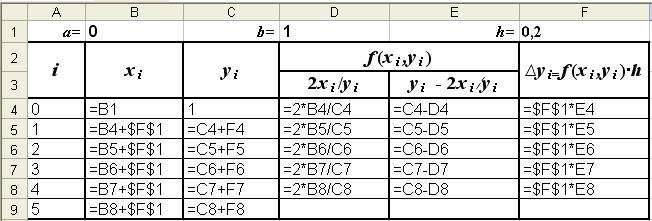
Режим решения

Рис. 1

Метод Эйлера легко распространяется на решение дифференциальных уравнений высших порядков. Для этого такое дифференциальное уравнение надо предварительно привести к дифференциальному уравнению первого порядка.

Пусть дано дифференциальное уравнение

y '' = f (x, y, y ') (4)

с начальными условиями

x = x ₀, у (x ₀) = y ₀, у' (x ₀) = y' ₀.

Требуется найти решение уравнения (4) на отрезке [ a, b ].

С помощью подстановки y' = z, y'' = z' заменим уравнение (4) системой уравнений

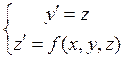и (5)

Таким образом, f ₁(x, y, z) = z, f ₂(x, y, z) = f (x, y, z) и задачу можно записать в общем виде:

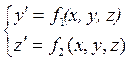и (6)

Аналогично можно свести к системе дифференциальных уравнений и уравнения более высокого порядка.

Пример 2. ○ Используя метод Эйлера, составить на отрезке [1; 1, 5] таблицу значений решения дифференциального уравнения

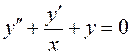(7)

с начальными условиями y = 0, 77, y ' = -0, 44 и выбрав шаг h = 0, 1.

Решение. С помощью подстановки y' = z, y'' = z' заменим уравнение (7) системой уравнений

y' = z,

с начальными условиями y ₀(1) = 0, 77 и z ₀ = -0, 44.

Таким образом,

f ₁(x, y, z) = z, f ₂(x, y, z) =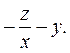

Результаты вычислений по формулам (6) запишем в таблице Excel (рис. 2). Заполняется она следующим образом:

в первую строку i = 0 запишем начальные условия: x ₀ = 1, 0, y ₀ = 0, 77, z ₀ = -0, 44.

Используя их, вычислим

f _{1 0}(x ₀, y ₀, z ₀) = z ₀ = -0, 44,

f _{2 0}(x ₀, y ₀, z ₀) =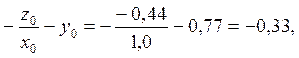

а затем

∆ y ₀ = h∙ f _{1 0} = 0, 1∙ (-0, 44) = -0, 044, y ₁ = y ₀ + ∆ y ₁ = 0, 77 + (-0, 044) = 0, 726,

∆ z ₀ = h∙ f _{2 0} = 0, 1∙ (-0, 33) = -0, 033, z ₁ = z ₀ + ∆ z ₁ = -0, 44 + (-0, 033) = -0, 473.

Таким образом, во вторую строку таблицы, соответствующую i = 1, можно записать:

y ₁ = 0, 726, z ₁ = -0, 473.

По этим значениям можно вычислить

f _{1 1}(x ₁, y ₁, z ₁) = z ₁ = -0, 473,

f _{2 1}(x ₁, y ₁, z ₁) =

а затем

∆ y ₁ = h∙ f _{1 1} = 0, 1∙ (-0, 473) = -0, 047, y ₂ = y ₁ + ∆ y ₁ = 0, 726 + (-0, 047) = 0, 679,

∆ z ₁ = h∙ f _{2 1} = 0, 1∙ (-0, 296) = -0, 030, z ₂ = z ₁ + ∆ z ₁ = -0, 473 + (-0, 030) =-0, 503.

Аналогично следует выполнять вычисления для i = 2, 3, 4, 5 (см. рис. 2).●

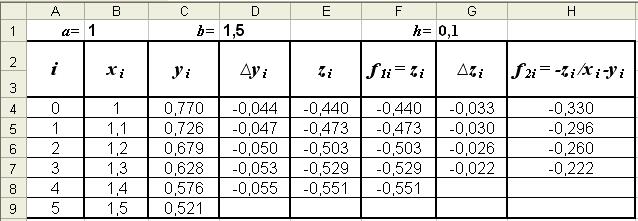
Режим формул

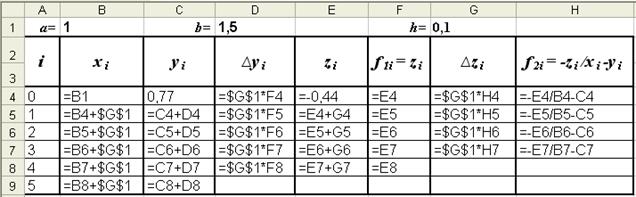
Режим решения

Рис. 2