
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Триметрическими – если все три коэффициента искажения по осям различны, т.е. когда k¹ m¹ n, и k ¹ n.
|
|

Рис. 7.1. Образование аксонометрической проекции предмета.
7.2. Стандартные аксонометрические проекции.
На практике используют аксонометрические проекции, которые кроме наглядности изображения обеспечивают простоту построения. К ним относятся прямоугольные аксонометрические проекции: изометрия и диметрия, а также косоугольные аксонометрические проекции: фронтальная диметрия и горизонтальная изометрия.
7.2.1. Прямоугольная изометрическая проекция.
В прямоугольной изометрической проекции коэффициенты искажения по всем трем осям одинаковы k= m= n. Используя формулу (*), считая, что 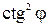 =0, получим:
=0, получим: 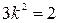 , тогда
, тогда 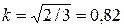 .
.
Следовательно, при построении изометрической проекции размеры предмета, откладываемые по аксонометрическим осям, умножаются на 0, 82. Такой перерасчет неудобен. Поэтому изометрическую проекцию для упрощения выполняют без уменьшения размеров (искажения) по осям, т.е. коэффициент искажения принимают равным 1. Получаемое при этом изображение предмета в изометрической проекции имеет несколько большие размеры, чем в действительности. Увеличение в этом случае составляет 22% и выражается числом 1, 22. Каждый отрезок, направленный по осям ОХ, OY, OZ, или параллельно им, сохраняет свою величину. Расположение осей, а также изображение детали в прямоугольной изометрической проекции показано на рис. 7.2.

Рис. 7.2. Расположение осей и пример изображения детали в прямоугольной изометрической проекции.
7.2.2. Прямоугольная диметрическая проекция.
Коэффициенты искажения в прямоугольной диметрической проекции выбирают следующими: k = n; m = 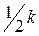 . Тогда, используя основную формулу аксонометрии, получим:
. Тогда, используя основную формулу аксонометрии, получим:
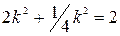 ;
; 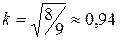 ;
; 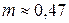 .
.
В целях упрощения построений, как и в изометрических проекциях, коэффициент искажения по осям ОХ и OZ принимают равным 1; по оси OY коэффициент искажения равен 0, 5. По осям ОХ и OZ, или параллельно им все размеры откладываются в натуральную величину, по оси OY - размеры уменьшают вдвое.
Увеличение в этом случае составляет 6% и выражается числом 1, 06. Расположение осей в прямоугольной диметрической проекции, а также пример изображения детали показан на рис.7.3. С достаточной для практических целей точностью оси ОХ и OY строят по тангенсам углов tg 7°10¢»1/8; tg 41°25¢»7/8.
Продолжение оси OY за центр О является биссектрисой угла XOZ, что также может быть использовано для построения оси OY.
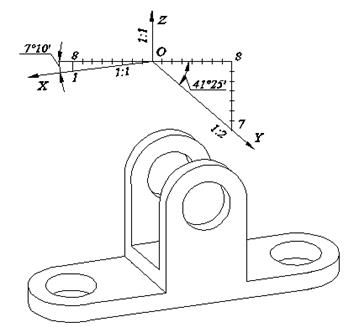
Рис. 7.3. Расположение осей и пример изображения детали в прямоугольной диметрической проекции.
7.3. Изображение окружности в аксонометрических проекциях
При построении аксонометрических проекций машиностроительных деталей часто приходится иметь дело с построением аксонометрических проекций окружностей. В большинстве случаев окружности лежат в плоскостях, параллельных какой-либо из координатных плоскостей. Рассмотрим примеры построения окружностей в прямоугольных изометрической и диметрической проекциях.
Представим себе окружности, вписанные в грани куба. На рис. 7.4 представлены проекции куба в изометрии и диметрии.
Окружность, вписанная в грани куба, касается его ребер в их середине. Из свойств параллельного проецирования известно, что если точка на отрезке делит его длину в заданном отношении, то и проекция точки делит одноименную проекцию отрезка в том же отношении. Значит в аксонометрических проекциях точки касания эллипсов, в которые преобразуются окружности, будут находиться также в серединах ребер куба. Кроме этих четырех точек можно указать еще четыре. В прямоугольных проекциях направление большой оси эллипсов перпендикулярны свободным аксонометрическим осям, а малые оси совпадают с ними по направлениям.
Для изометрии величина большого диаметра эллипса равна 1, 22 d окружности, малого диаметра - 0, 71 d. В диметрии большой диаметр эллипса равен 1, 06 d, а малый диаметр для эллипсов, расположенных в плоскостях параллельных координатным плоскостям XOY и YOZ, равен 0, 35 d. Для эллипсов, расположенных параллельно плоскости XOZ, малый диаметр равен 0, 95 d.
При построении аксонометрических изображений в изометрической проекции, эллипсы можно заменить овалами.
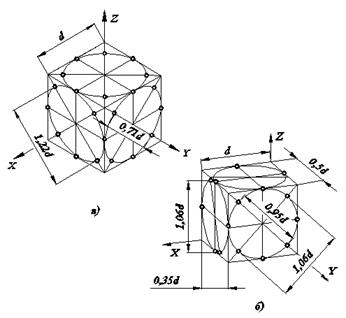
Рис.7.4. Изображение окружностей в аксонометрической и диметрической проекции.
Вопросы для самоконтроля:
4. Как получают аксонометрическую проекцию?
5. Какие виды аксонометрических проекций вы знаете?
6. Чем характеризуется прямоугольная изометрия?
4. Как построить изометрию окружности?.
5. Что называется коэффициентом искажения аксонометрической проекции?